Virtual Work/Unit Load Method

The Virtual Work Method is based on the principle of energy conservation. It equates the virtual external work done by a unit force or moment to the virtual internal work done by internal stresses and deformations.

Strain Energy

When a force acts on an elastic body, it stores energy as strain energy. For a linear elastic material:

When the force increases linearly from 0 to $P$:
$$ W = \frac{1}{2} P \Delta $$
When the force is constant:
$$ W = P \Delta $$

Similarly, for moments causing rotation:

Linearly increasing moment:
$$ W = \frac{1}{2} M \theta $$
Constant moment:
$$ W = M \theta $$

Principle of Virtual Work

$$ \text{Virtual External Work} = \text{Virtual Internal Work} $$

More specifically: $$ (\text{real displacement}) \times (\text{virtual force}) = (\text{real internal displacement}) \times (\text{virtual internal force}) $$

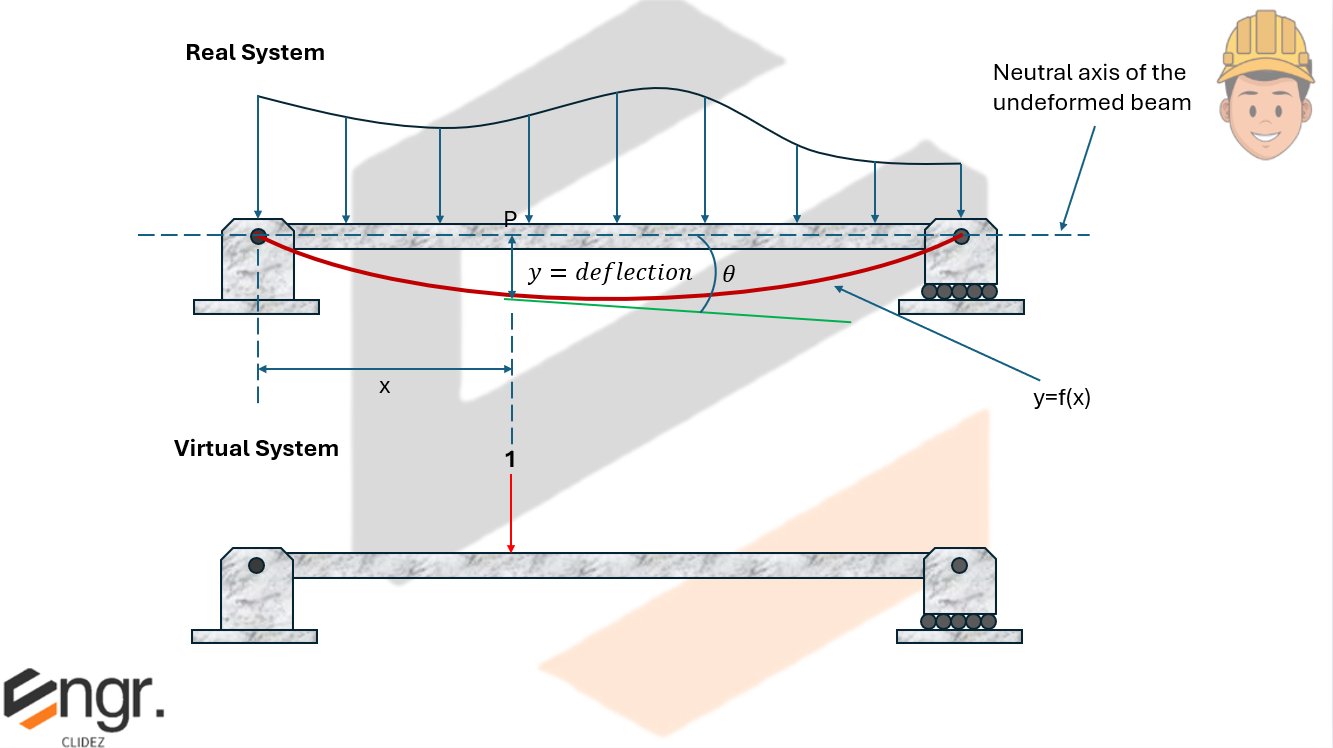
Virtual Work for Deflection and Rotation in Beams

To compute the deflection $\Delta$ at a point, apply a unit load at that point in the direction of the desired deflection. Then:

$$ \delta = \int_0^L \frac{M \cdot M_v}{EI} \, dx $$

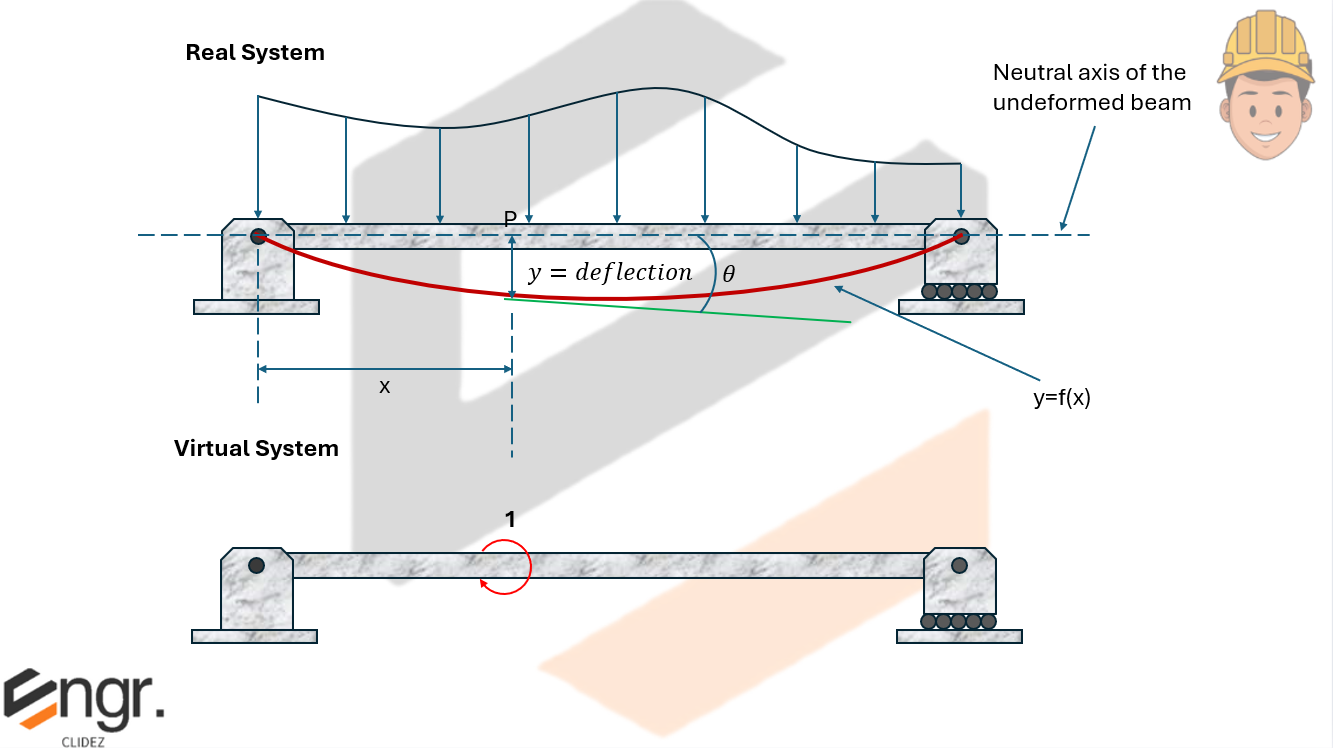
To compute the rotation $\theta$ at a point, apply a unit moment (couple) at that point in the direction of the desired rotation. Then:

$$ \theta = \int_0^L \frac{M \cdot M_v}{EI} \, dx $$

Where:

$M$ is the moment from the real loading
$M_v$ is the moment from the virtual system unit load or moment
$EI$ is the flexural rigidity of the beam

Summary of Procedure

Identify the location and type of displacement or rotation to be found.
Apply a unit load for deflection or unit moment for rotation at that location and direction.
Find internal moment expressions $M$ and $M_v$ for both the real and virtual systems across each segment.
Use the integral
$$ \int_0^L \frac{M \cdot M_v}{EI} dx $$
to find the desired deflection or rotation.