Three Moment Equation

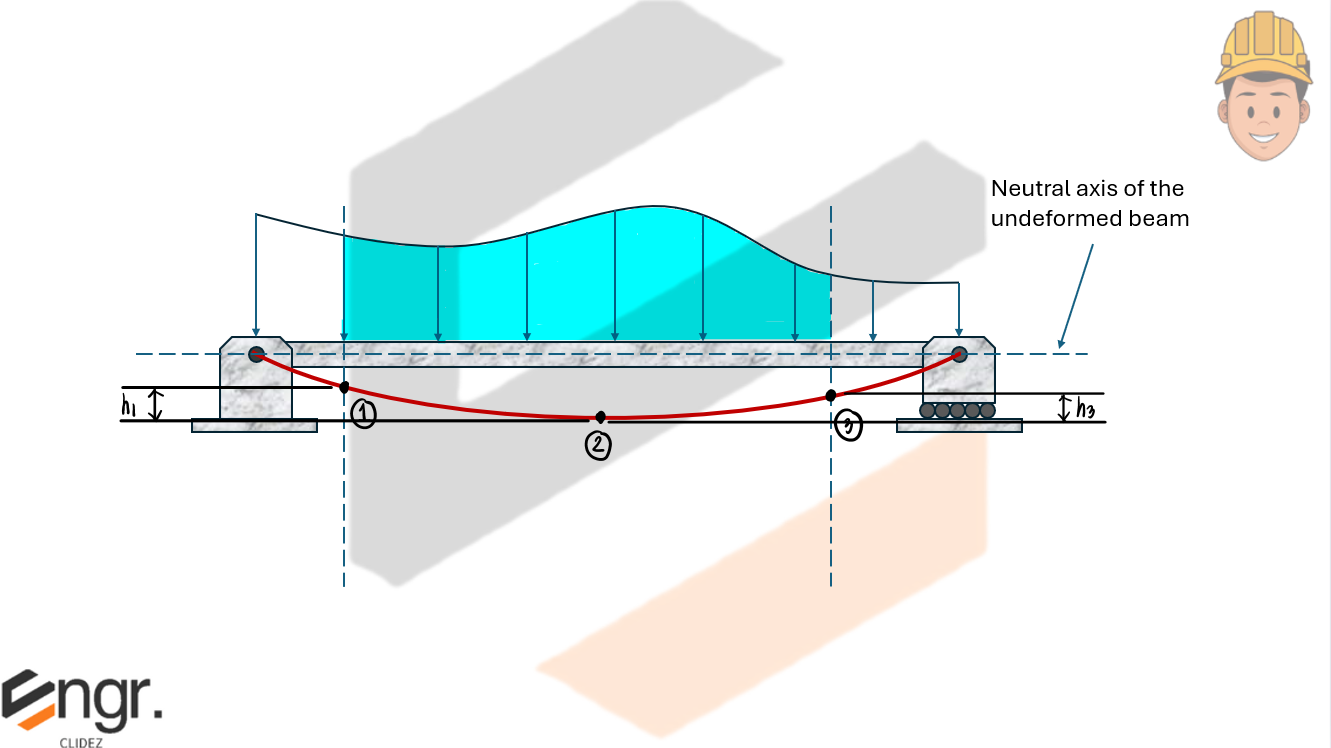
The Three-Moment Equation is used to analyze continuous beams with multiple spans. It relates the bending moments at three consecutive points of a continuous beam and includes the effects of support settlements and external loads.

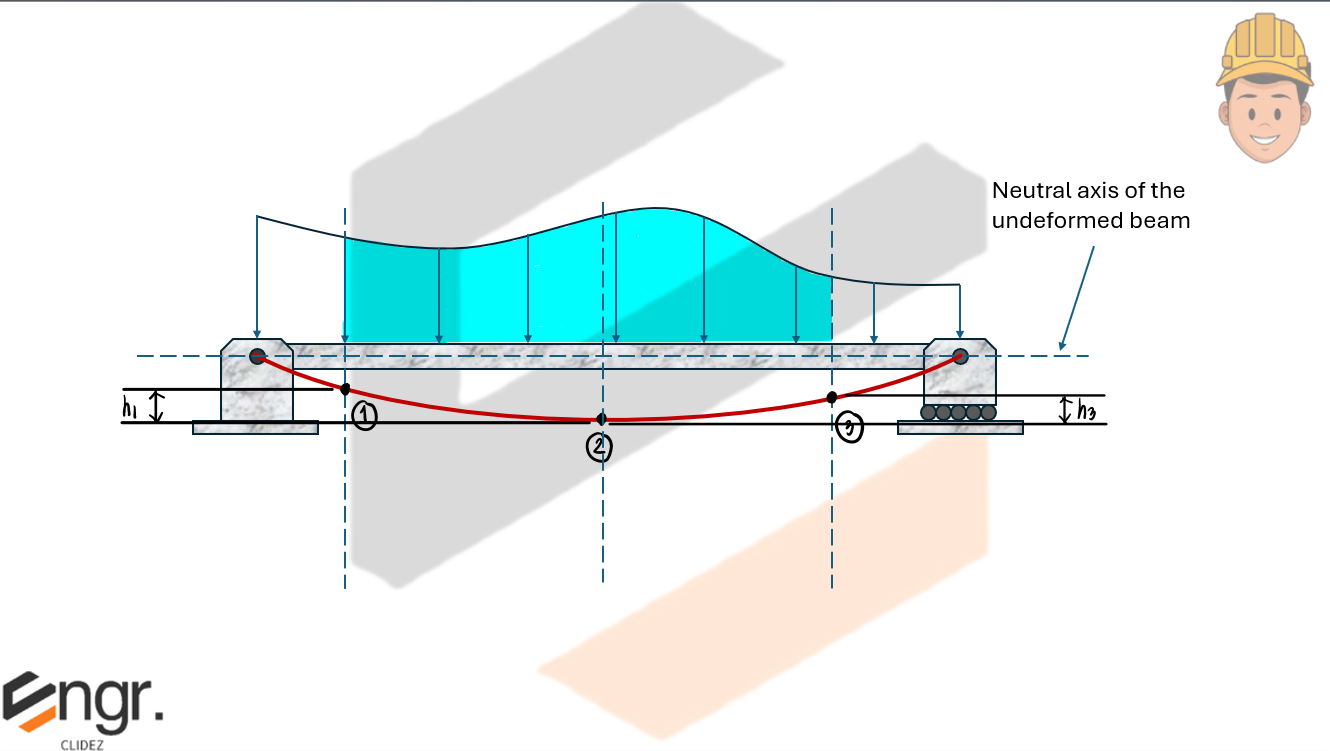
Geometric Compatibility: Similar Triangles

From geometry, we relate vertical distances at the extreme points using similar triangles:

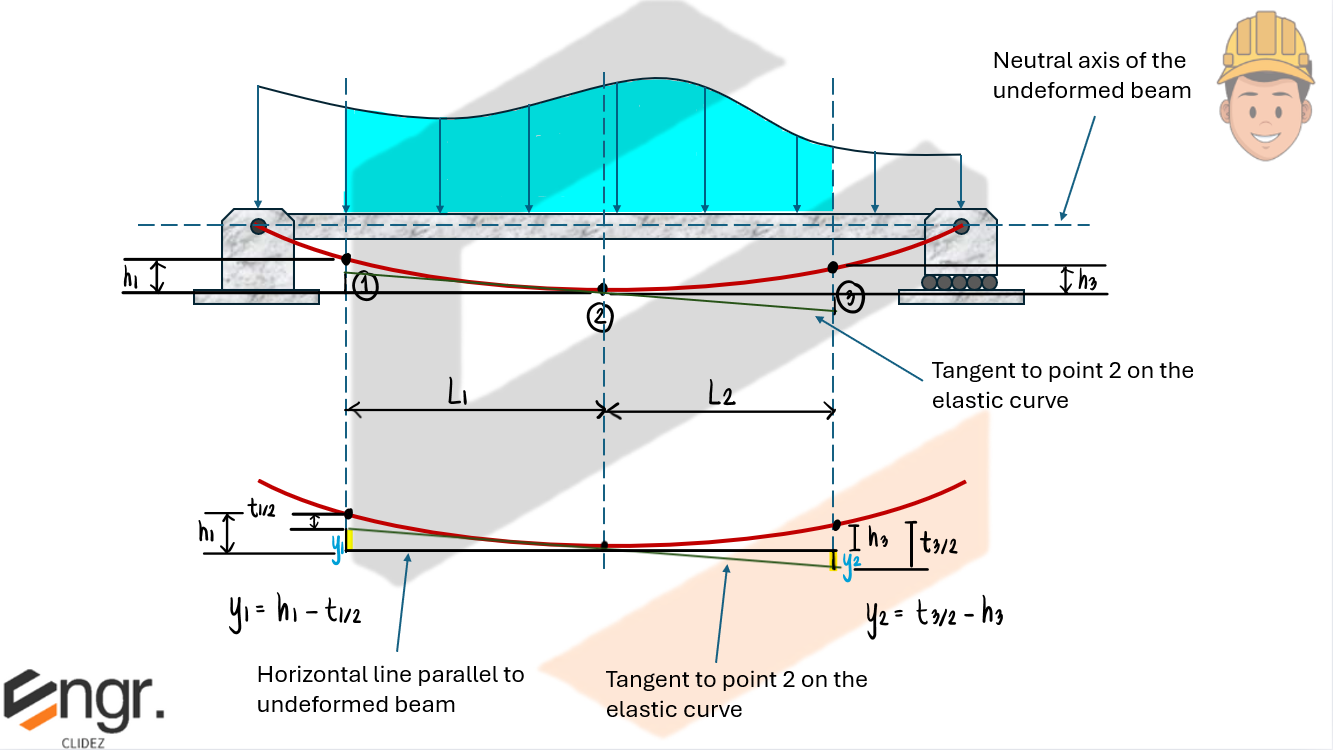
From proportions between similar triangles:

$$ \frac{h_1 - t_{1/2}}{L_1} = \frac{t_{3/2} - h_3}{L_2} $$

Expanding the fractions:

$$ \Rightarrow \frac{h_1}{L_1} - \frac{t_{1/2}}{L_1} = \frac{t_{3/2}}{L_2} - \frac{h_3}{L_2} $$

$$ \Rightarrow \frac{t_{1/2}}{L_1} + \frac{t_{3/2}}{L_2} = \frac{h_1}{L_1} + \frac{h_3}{L_2} \quad \text{→ Equation (1)} $$

Moment Area Calculations for Tangents

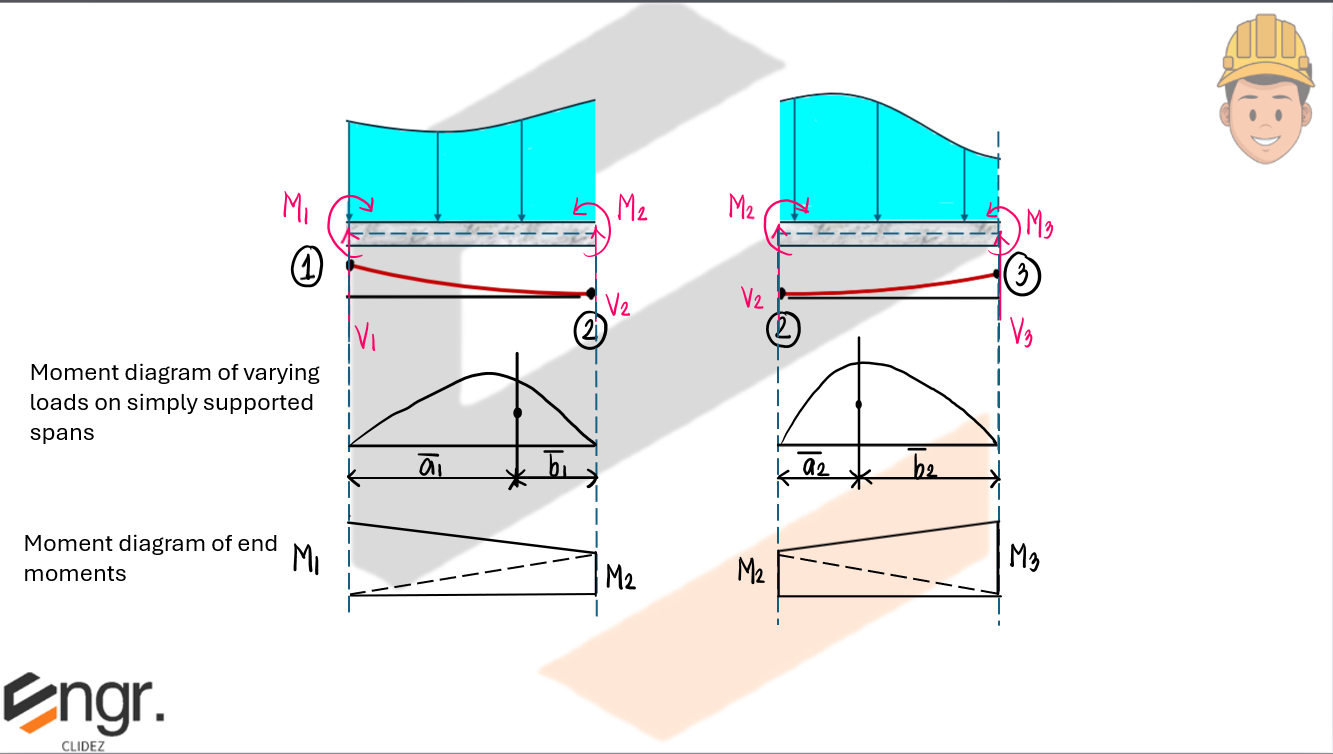
The tangent distances $t_{1/2}$ and $t_{3/2}$ are computed using area and centroid of the moment diagram between supports:

$$ t_{1/2} = \frac{1}{E_1 I_1} (A_{1} \bar{a}_1 + M_1 L_1 + 2M_2 L_1) \cdot \frac{1}{6} $$

$$ t_{3/2} = \frac{1}{E_2 I_2} (A_{2} \bar{b}_2 + 2M_2 L_2 + M_3 L_2) \cdot \frac{1}{6} $$

Substitute into Compatibility Equation

Substitute $t_{1/2}$ and $t_{3/2}$ into Equation (1):

$$ \frac{1}{6 E_1 I_1} \left( \frac{6 A_1 \bar{a}_1}{L_1} + M_1 L_1 + 2M_2 L_1 \right) + \frac{1}{6 E_2 I_2} \left( \frac{6 A_2 \bar{b}_2}{L_2} + 2M_2 L_2 + M_3 L_2 \right) = \frac{h_1}{L_1} + \frac{h_3}{L_2} $$

Final Simplified Three Moment Equation

Multiplying through by 6 and distributing $1/EI$ yields:

$$ \frac{M_1 L_1}{E_1 I_1} + 2M_2 \left( \frac{L_1}{E_1 I_1} + \frac{L_2}{E_2 I_2} \right) + \frac{M_3 L_2}{E_2 I_2} + \frac{6 A_1 \bar{a}_1}{E_1 I_1 L_1} + \frac{6 A_2 \bar{b}_2}{E_2 I_2 L_2} = 6 \left( \frac{h_1}{L_1} + \frac{h_3}{L_2} \right) $$

$M_1, M_2, M_3$ are the bending moments at the three consecutive points
$L_1, L_2$ are the lengths of the adjacent spans
$E_1I_1, E_2I_2$ are the flexural rigidities of the spans
$A_1, A_2$ are the areas under the moment diagrams of the spans
$\bar{a}_1, \bar{b}_2$ are the distances of centroids of those areas from the respective points
$h_1, h_3$ are the vertical settlements at the chosen points

When $EI$ is constant across spans, common in many problems:

$$ M_1L_1 + 2M_2(L_1 + L_2) + M_3L_2 + \frac{6A_1\bar{a}_1}{L_1} + \frac{6A_2\bar{b}_2}{L_2} = 6EI\left( \frac{h_1}{L_1} + \frac{h_3}{L_2} \right) $$

This simplified version assumes a uniform flexural rigidity $EI$, allowing quicker calculation. Note that all areas $A$, distances to centroids --> $\bar{a}, \bar{b}$, and moments must still be computed per segment if loading varies.