Moment Distribution Method

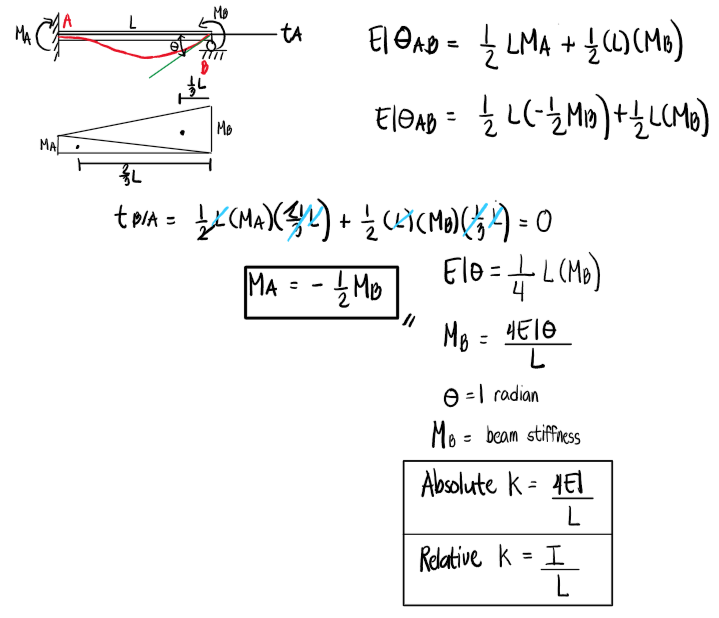
The Moment Distribution Method, developed by Hardy Cross, is a powerful technique for analyzing indeterminate beams and frames. It simplifies solving by balancing moments at joints through successive approximations, eliminating the need to solve large systems of equations.

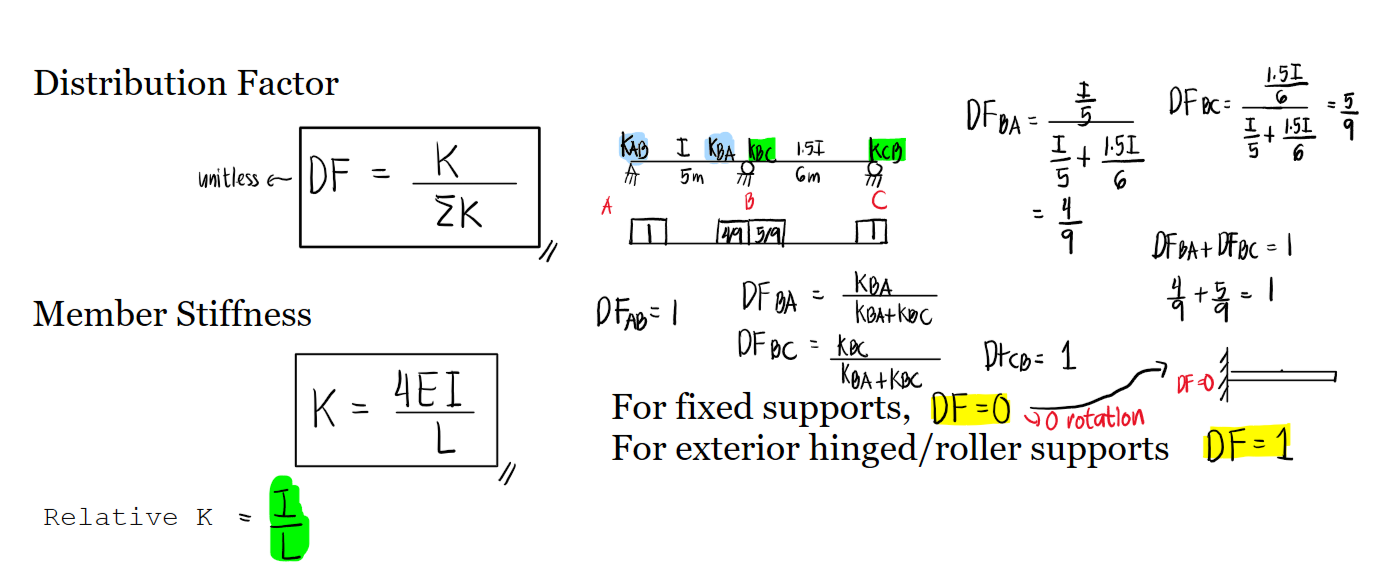
Key Concepts

Stiffness (K): Measures a member’s resistance to rotation. Given by:
$$ K = \frac{4EI}{L} $$

$$ \text{Relative Stiffness} = \frac{I}{L} $$
Distribution Factor (DF): Ratio of a member’s stiffness to the total stiffness at a joint.
$$ DF = \frac{K}{\Sigma K} $$

For fixed supports, DF = 0 --> no rotation.
For hinged or roller ends, DF = 1 --> full moment transfer.
Carry-Over Moment (COM): Half of the moment at one end is transferred to the other end of the member.
$$ M_A = -\frac{1}{2} M_B $$
Modified Stiffness: For members with a hinged or roller end, modify the relative stiffness, $I/L$, using:
$$ K_{\text{mod}} = \frac{3}{4} \cdot \frac{EI}{L} = \frac{3EI}{4L} $$

Fixed-End Moment Formulas and Support Settlement

Free Ends

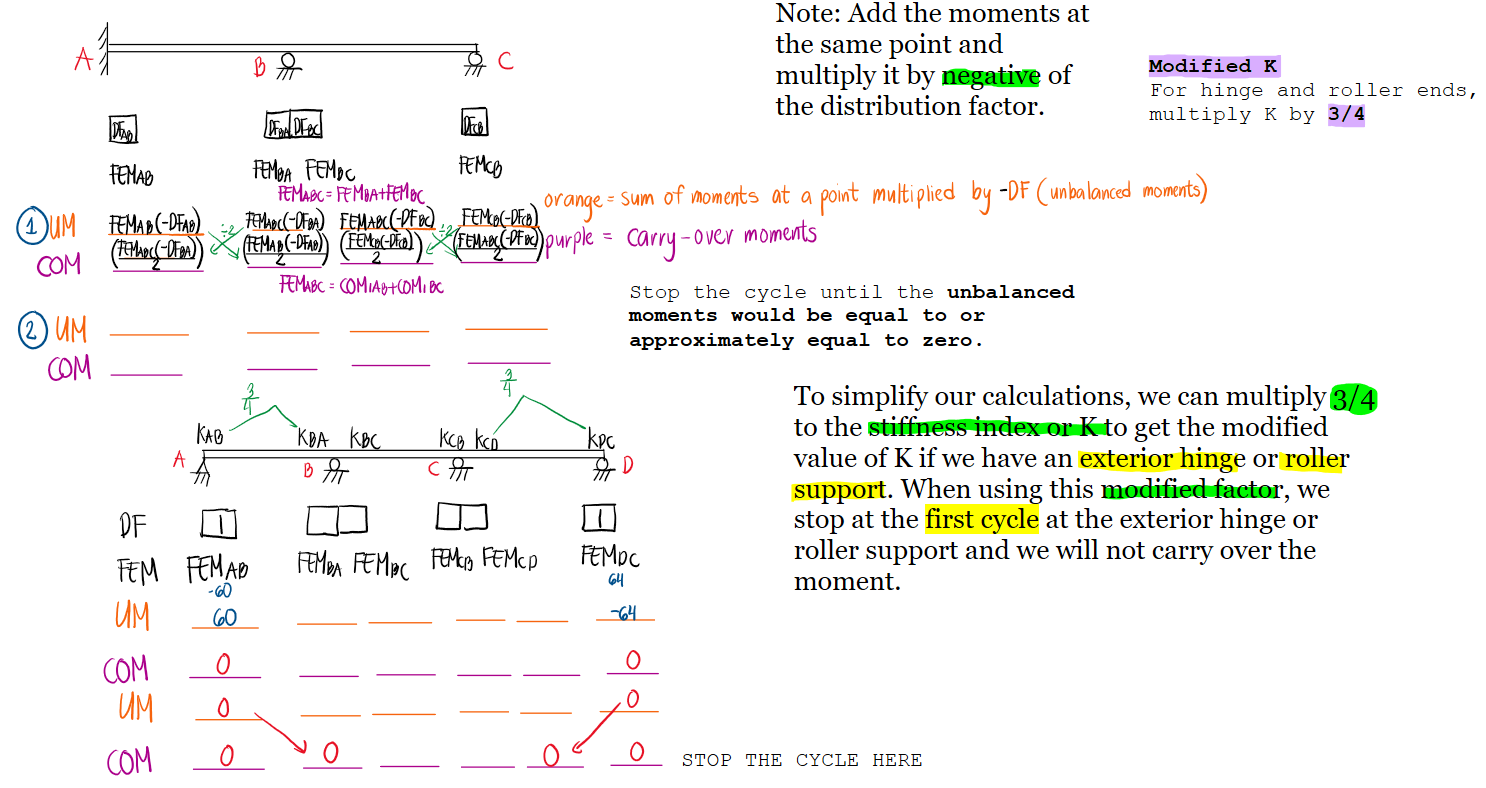
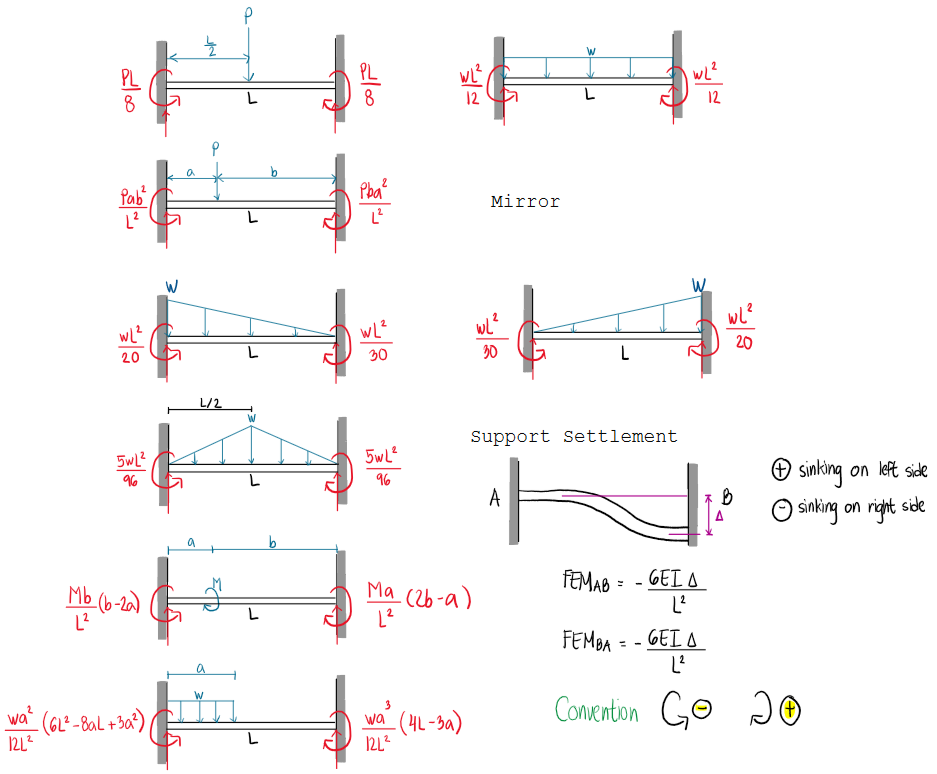
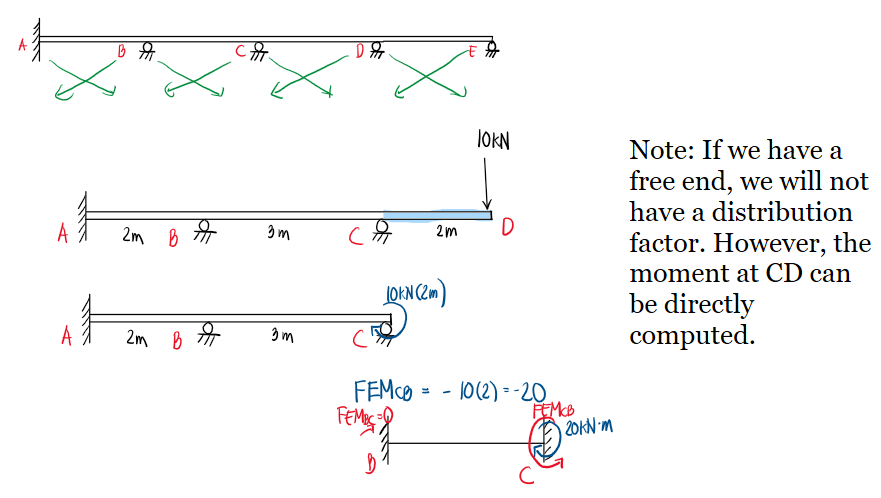
If a member terminates at a free end, no moment is distributed from that joint. However, you can compute the end moment directly using:

$$ M = F \cdot d $$

Problem 1: Beam with Support Settlement - Sinking of Supports

Calculate the support reactions of the beam shown using the Modified Method and the Adjusted F.E.M. if the support at A sinks by 7mm and the support at B sinks by 12mm. E=12GPa and I=125x10⁷mm⁴

See images:

The above solution does not use the modified method, but we are showing it to demonstrate how the modified method simplifies the process. Below is the solution using the Modified Method.

The reactions of the beams are also solved below using the calculated end moments.

Problem 2: (Beam with Overhang)

Calculate the support reactions of the beam shown.

See images:

Problem 3: (Distributed Load and Load at the Midspan)

Calculate the support reactions of the beam shown.

See images:

Problem 4: (Moment Distribution Method for Frames)

Calculate the reactions of the frame shown using Moment Distribution Method

See images:

Problem 5: (Moment Distribution Method for Frames)

Determine the moments acting at the ends of each member. Assume B is a fixed joint and A and D are pin supported and C is fixed. E=29x10³ksi. I_ABC=700in⁴ and I_BD=1100in⁴

See images: