Beam deflection refers to the displacement of a structural element under load. Understanding how beams bend and deform is essential for ensuring structural safety and serviceability. In engineering, various methods are used to calculate beam deflections, each suited for specific types of loads, supports, and material behavior. One fundamental method is the Double Integration Method, which uses calculus and moment equations to determine the slope and deflection along the length of the beam.
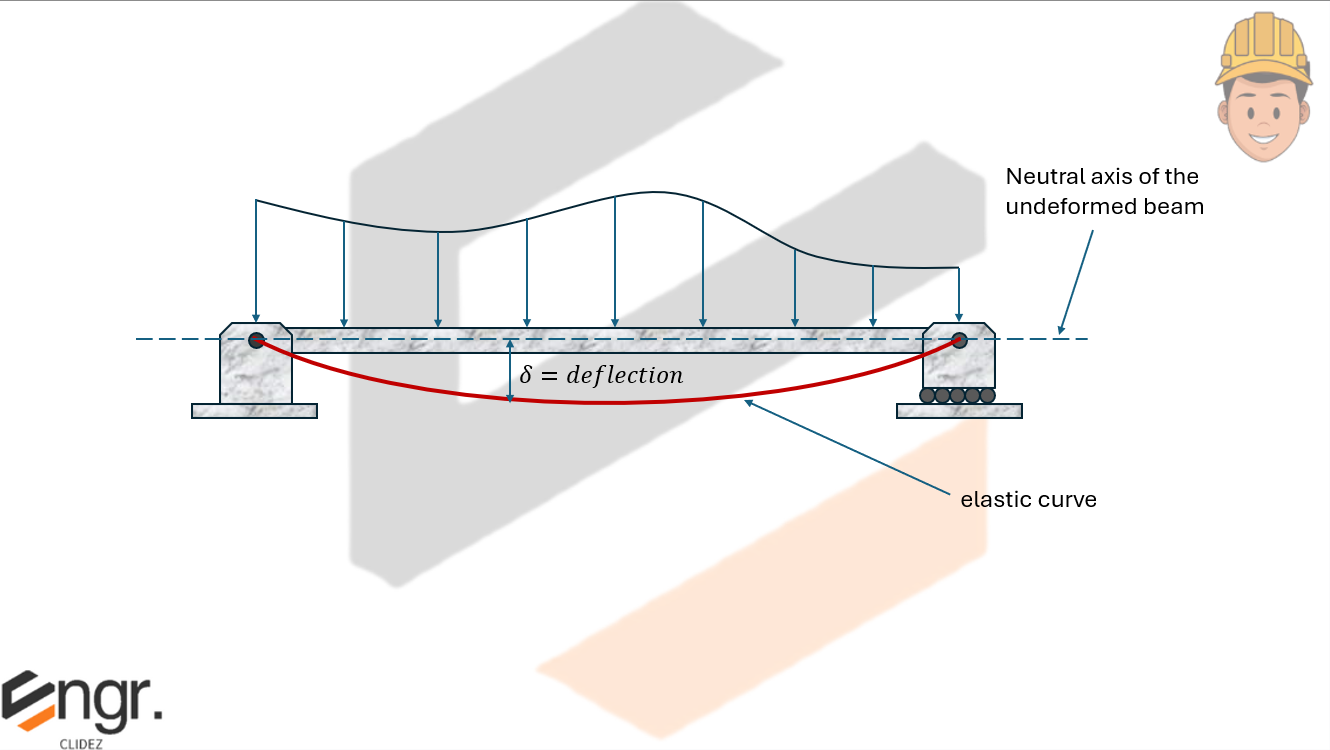
Setting the left end as the origin for the beam, at point \( P \), a distance \( x \) from the origin, the deflection is \( y \) and the slope of the elastic curve is \( \theta \).
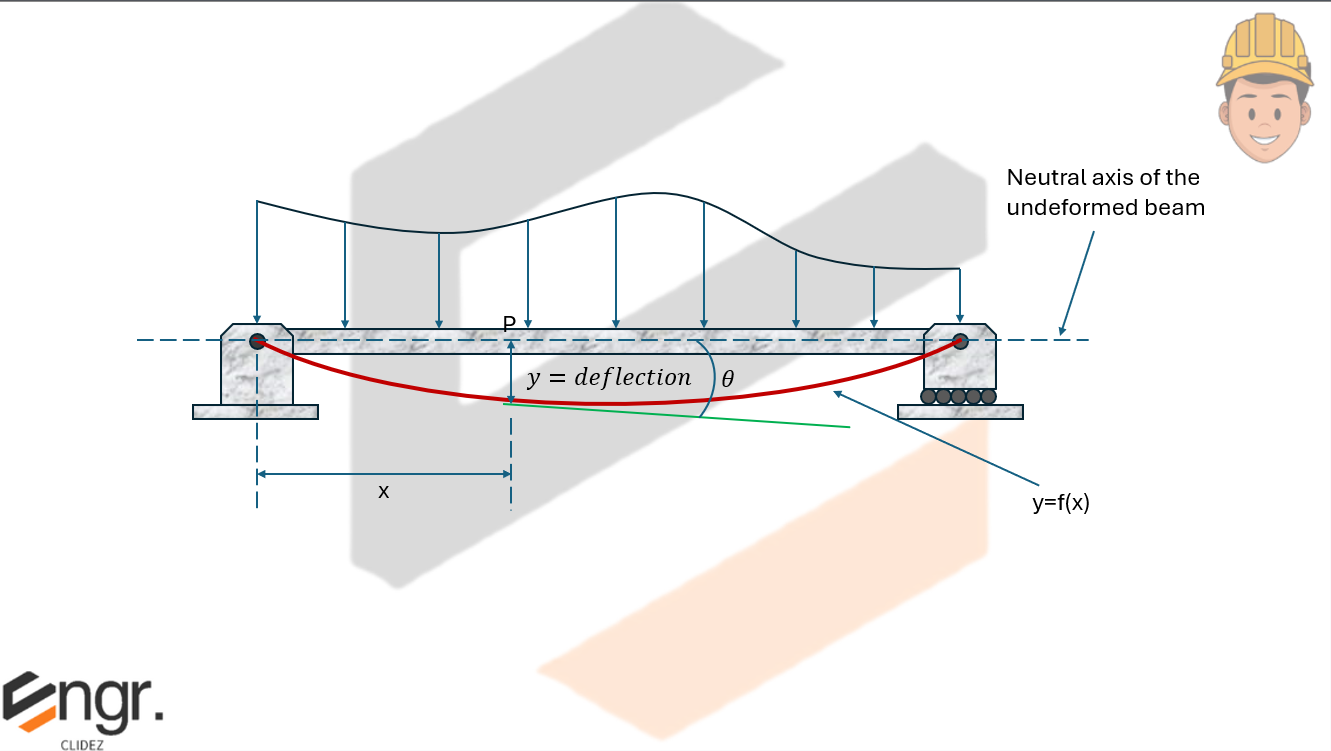
Let \( y = f(x) \) be the equation of the elastic curve. From calculus, the radius of curvature of a curve \( y = f(x) \) is given by the formula:
Deflection of beams is so small that the slope \( \dfrac{dy}{dx} \) is very small, and squaring it gives approximately zero. Hence, we have:
From Strength of Materials, the radius of curvature of the beam subjected to bending is:
Equating the two expressions for \( \rho \), we have:
or
Equation above is known as the differential equation of the elastic curve.
Where:
\( E \) = modulus of elasticity of the beam material
\( I \) = moment of inertia of the beam cross-section
\( EI \) = flexural rigidity (product of \( E \) and \( I \))
\( M \) = bending moment at the point \( P \)
The first integration gives:
This is the slope equation. Note that \( \tan \theta = \dfrac{dy}{dx} \), but for small angles, \( \tan \theta \approx \theta \), thus:
Note that \( \theta \) is also the rotation of the beam at the given point.
The second integration gives:
This is called the deflection equation, where \( C_1 \) and \( C_2 \) are constants of integration that can be solved using known boundary conditions.







For the beam shown, determine:
a. The slope at point D
b. The deflection at the free end (point E)
c. The location of the maximum deflection midway between B and D
d. The value of the maximum deflection considering the previous question



See images:




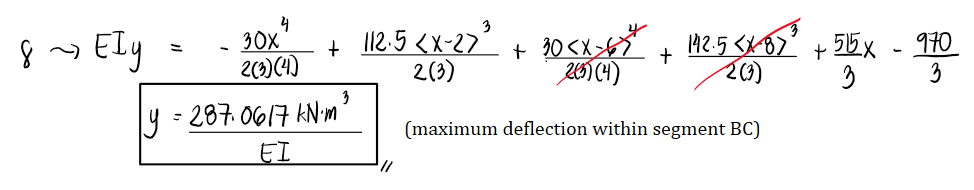
For the beam shown, determine:
a. The slope at D
b. The deflection at C



See images:




For the beam shown, determine:
a. The slope at point C
b. The deflection at point C



See images:




For the beam shown, determine:
a. The slope at point C
b. The deflection at the free end
c. The location and value of the maximum deflection midway between AC



See images:




Problem by Engr. Edwin Rosalena
a. For the beam shown, compute the deflection at a point 2m from the left support.
b. Compute the maximum deflection.
c. Compute the slope (rotation) at the free end.



See images:




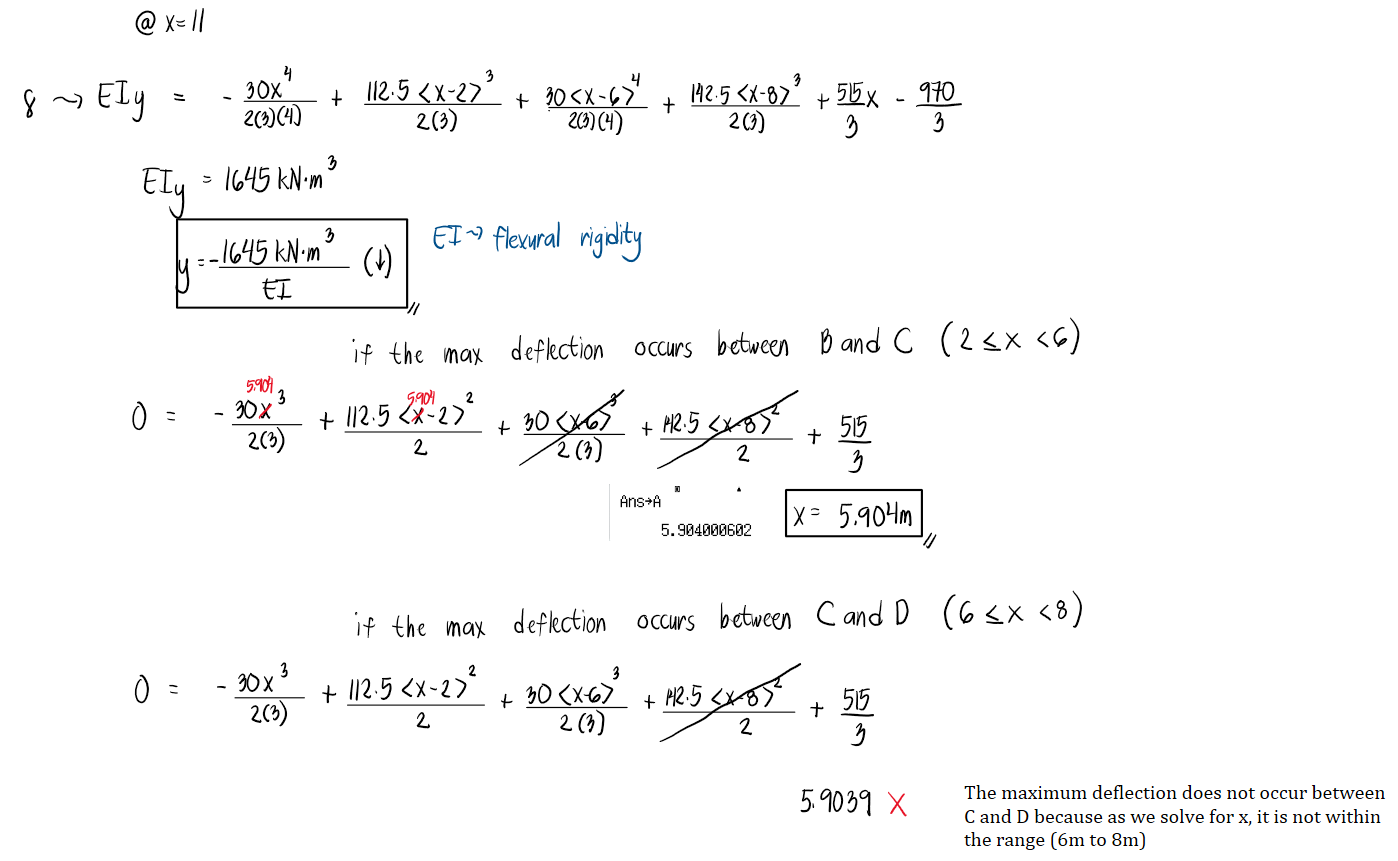
For the beam shown,
a. Determine the deflection at the free end.
b. Determine the location of the maximum deflection.
c. Determine the maximum deflection.
d. Determine the slope at the roller support.



See images:






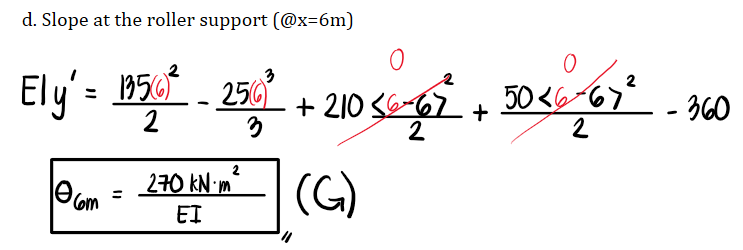
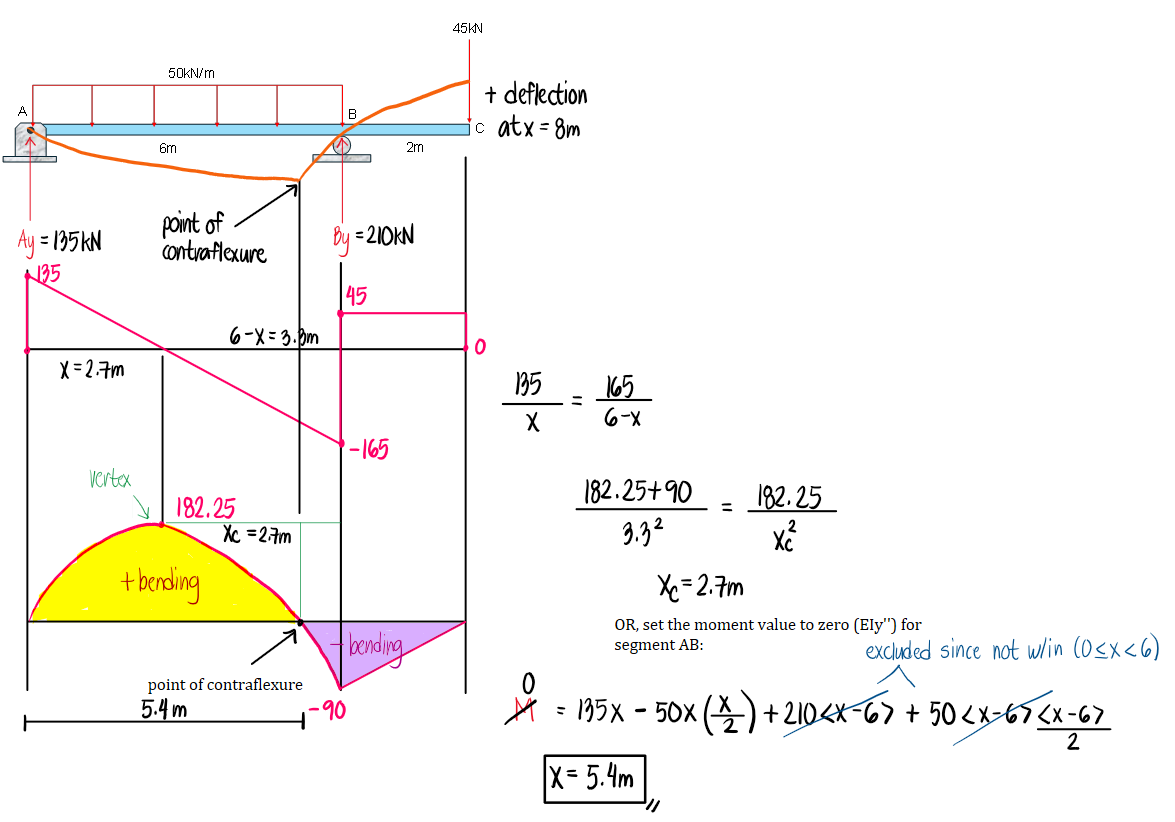
For the beam shown, use E = 200GPa and I = 20x106mm4.
Draw the shear and moment diagram as well as the elastic curve.
a. Compute the deflection at D (in mm).
b. Compute the deflection at A (in mm).
c. Compute the left and right slope values at D (in degrees).



See images:




The simply supported steel beam is loaded by the 20kN-m couple as shown in the figure. Using E = 200GPa and I=8x10-4m4, determine the displacement and slope at the point where the couple is applied. Use Double Integration Method.



See images:




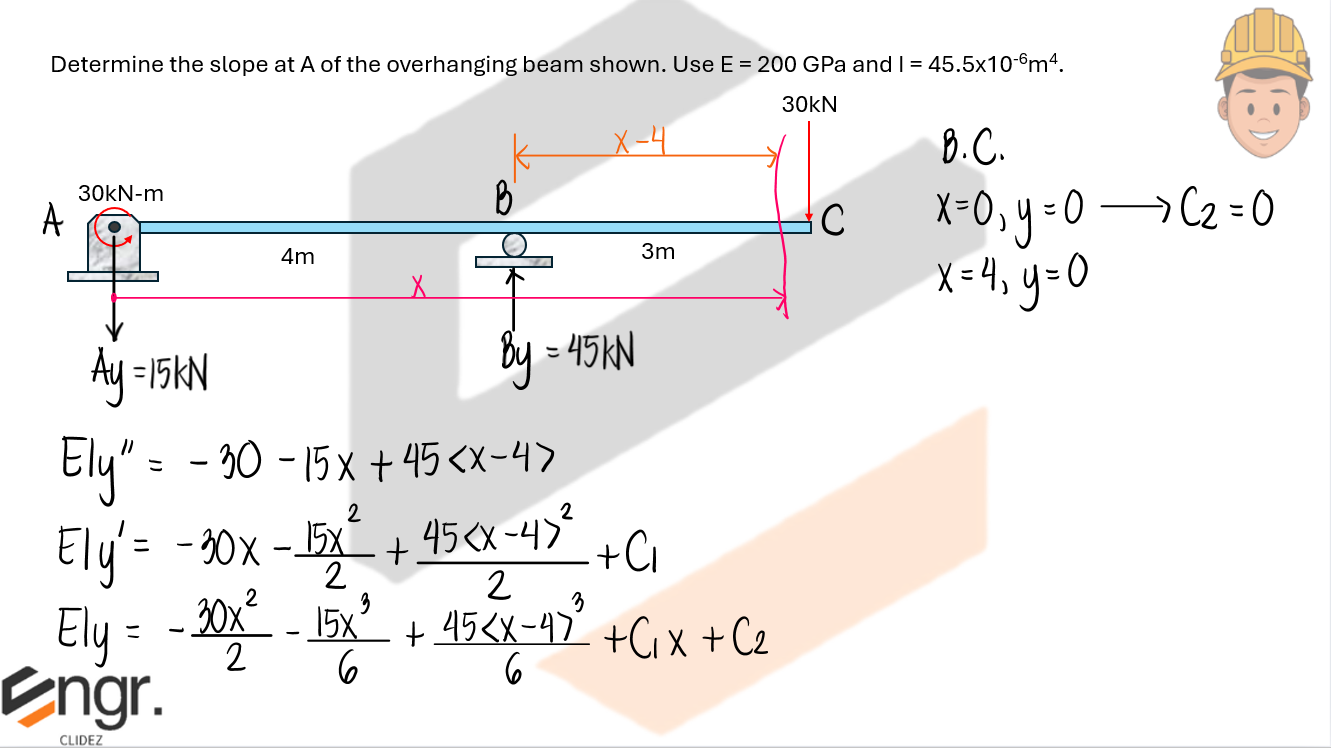
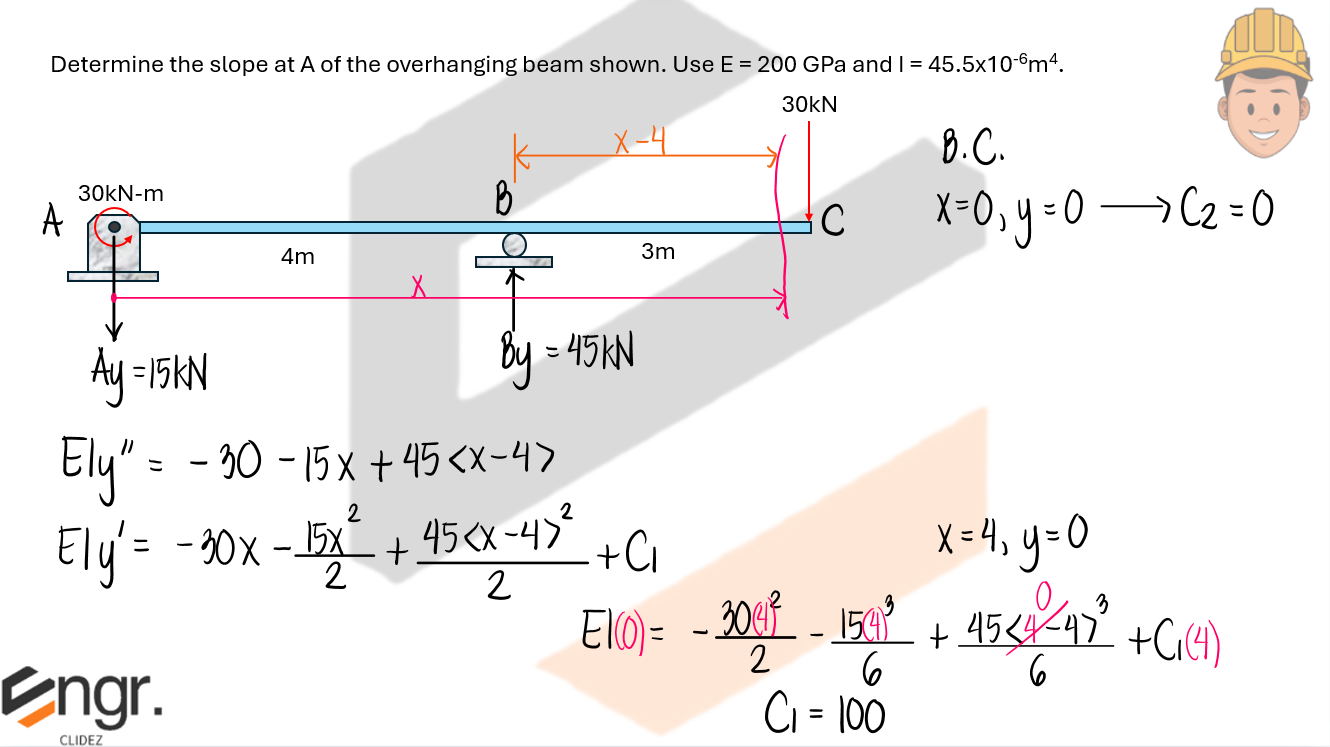
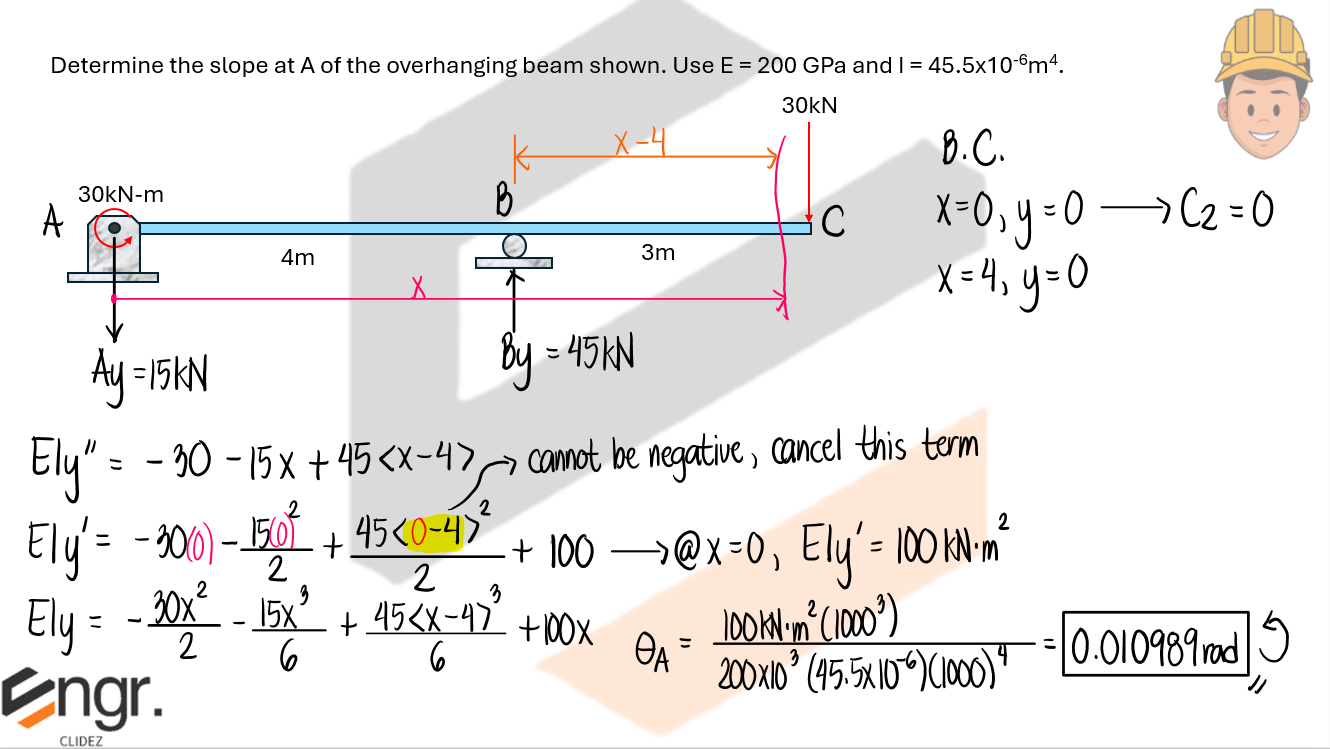
Determine the slope at A of the overhanging beam shown. Use E = 200GPa and I = 45.5x10-6mm4
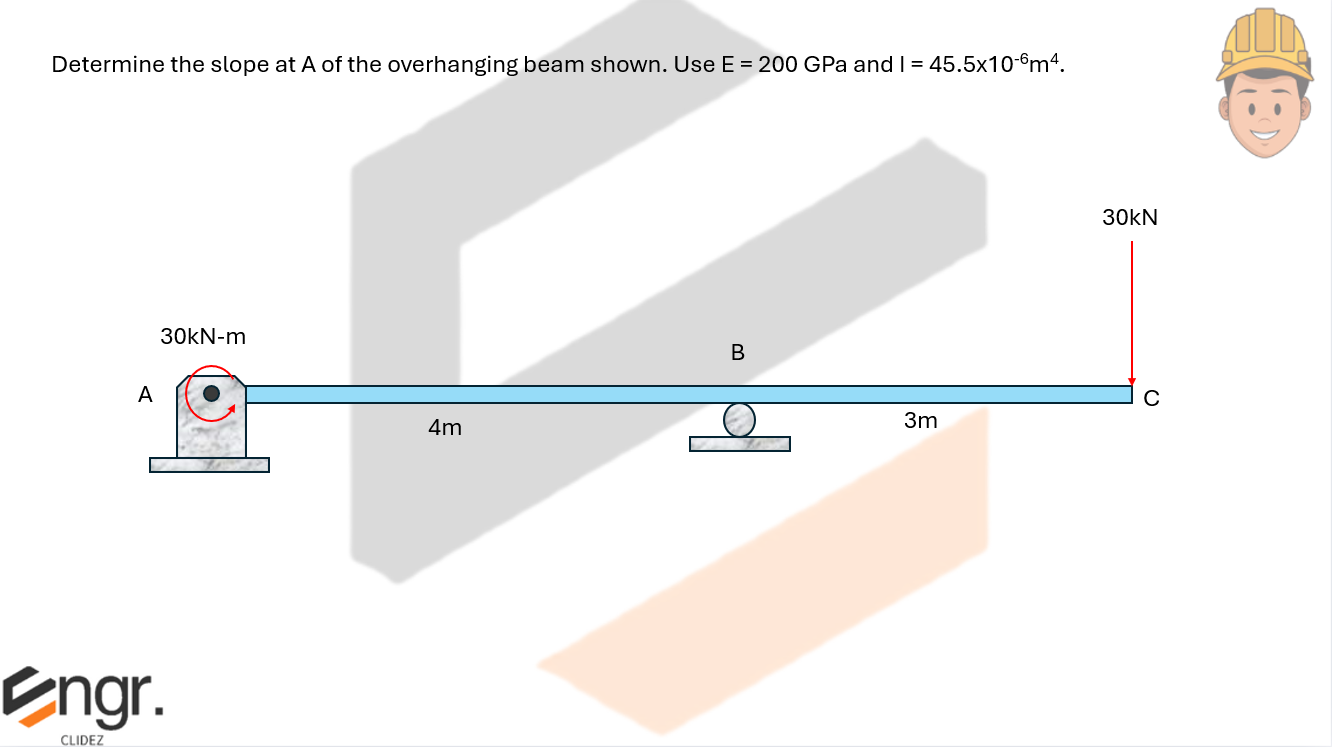


See images: