The Conjugate Beam Method is a powerful technique used to determine the slope and deflection in a real beam by analyzing a related, imaginary beam called the conjugate beam.
To understand this method, we compare two sets of relationships:
From the double integration method, we recall the following relationships:
Moment-curvature relation:
Slope equation:
Deflection equation:
These equations show that moment, slope, and deflection follow a pattern similar to load, shear, and moment in statics. Hence, we establish the following analogy:
The real beam is the actual structure under load. The conjugate beam is a hypothetical beam loaded with the moment diagram divided by $EI$, and its support conditions are chosen to reflect the slope and deflection behavior of the real beam.
Important: The resulting conjugate beam may be statically unstable from a structural perspective — for example, a real beam with fixed supports at both ends will lead to a conjugate beam with free ends. Despite appearing unstable, the conjugate beam must be solved as-is because it reflects the correct mathematical relationships between slope and deflection in the real beam.
Key idea: The supports of the conjugate beam must be modified so that:
By designing the conjugate beam accordingly and applying the moment/$EI$ diagram as loading, we can compute the slope and deflection in the real beam by analyzing the shear and moment values in the conjugate beam.
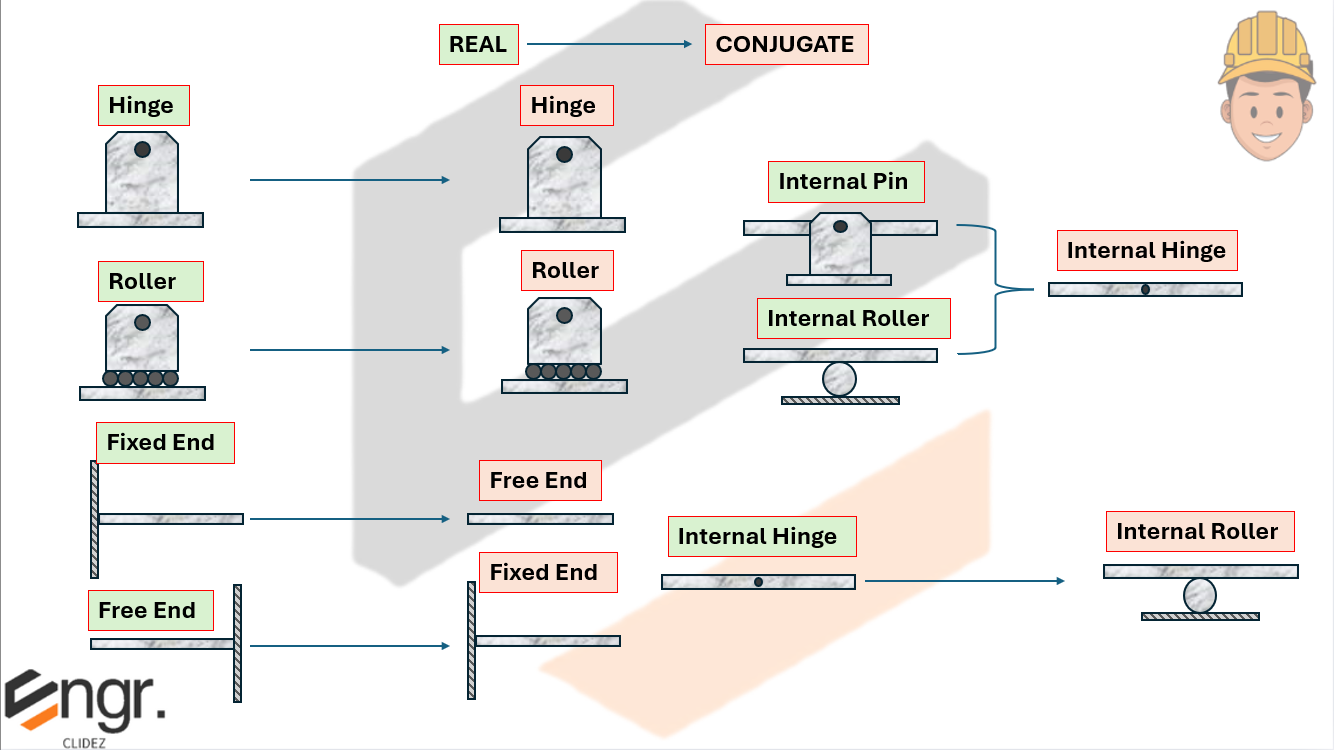
| Real Beam Support | Slope $\theta$ | Deflection $y$ | Conjugate Beam Support | Conjugate Shear $V$ | Conjugate Moment $M$ |
|---|---|---|---|---|---|
| Fixed End | $\theta = 0$ | $y = 0$ | Free End | $V = 0$ | $M = 0$ |
| Free End | $\theta \ne 0$ | $y \ne 0$ | Fixed End | $V \ne 0$ | $M \ne 0$ |
| Hinge | $\theta \ne 0$ | $y = 0$ | Hinge | $V \ne 0$ | $M = 0$ |
| Roller | $\theta \ne 0$ | $y = 0$ | Roller | $V \ne 0$ | $M = 0$ |
| Internal Pin | $\theta \ne 0$ | $y = 0$ | Internal Hinge | $V \ne 0$ | $M = 0$ |
| Internal Roller | $\theta \ne 0$ | $y = 0$ | Internal Hinge | $V \ne 0$ | $M = 0$ |
| Internal Hinge | $\theta \ne 0$ | $y \ne 0$ | Internal Roller | $V \ne 0$ | $M \ne 0$ |
General rule: If a real support allows a slope, the conjugate support must develop a shear, and if the real support allows a displacement, the conjugate support must develop a moment.








For the beam shown, using the Conjugate Beam Method:
a. Determine the slope at A.
b. Determine the deflection at B.
c. Determine the location and value of the maximum deflection.



Moment Diagram by Parts




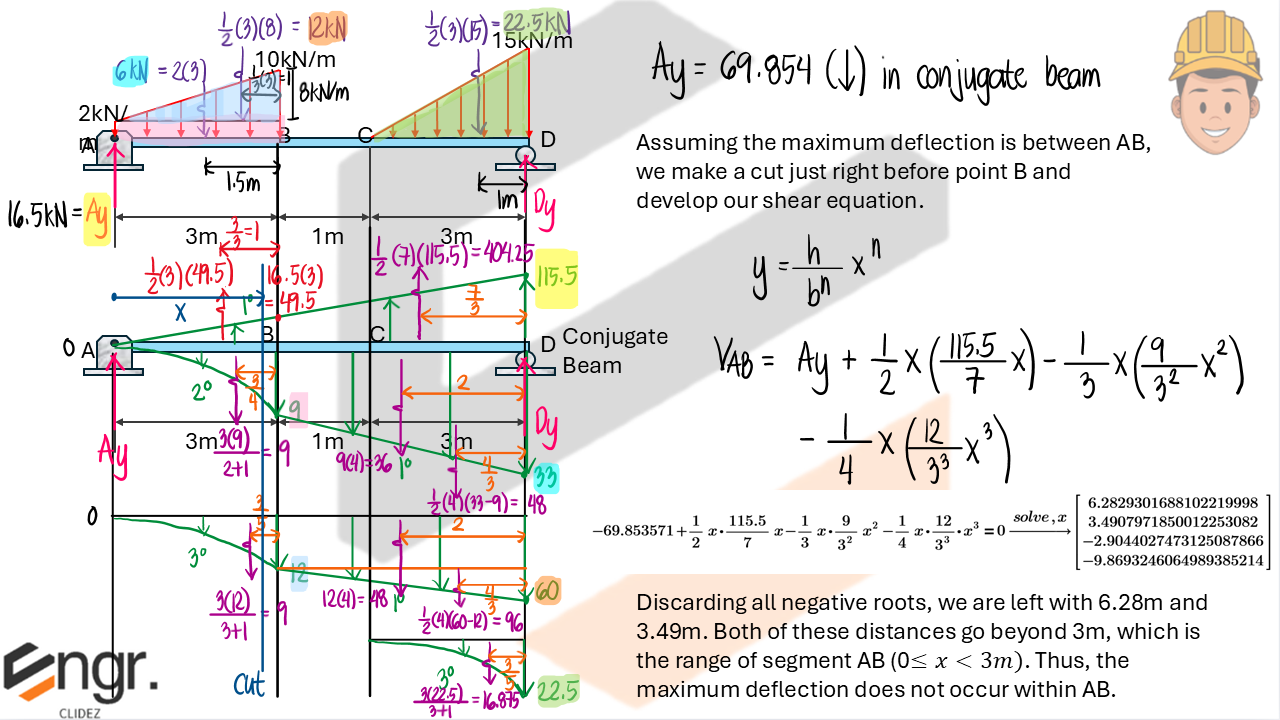
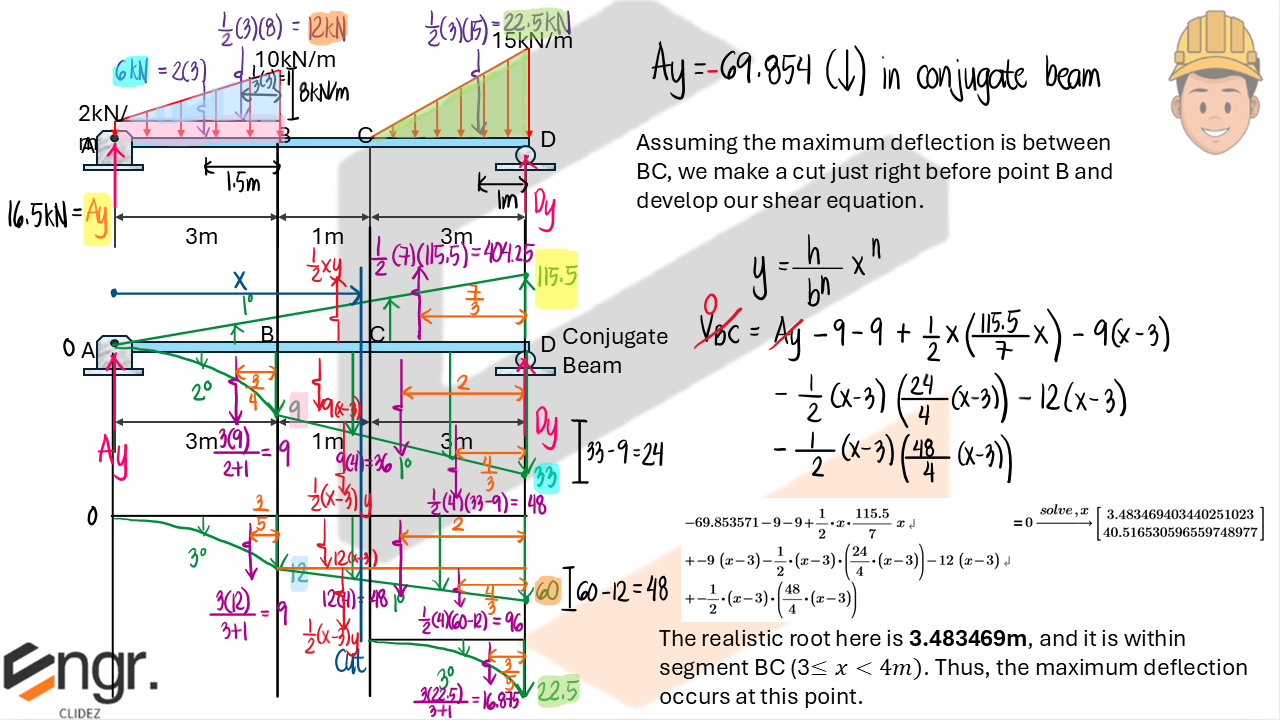
For the beam shown, determine the following:
a. The deflection at the free end
b. The location of the maximum deflection
c. The maximum deflection
d. The slope at the roller support



See images:




Refer to the image shown:



See images:




Refer to the image shown:



See images:




Refer to the image shown:



See images:




Refer to the image shown:



See images:




Refer to the image shown:



See images:




Refer to the image shown:



See images:



