Castigliano's Second Theorem

Castigliano’s Theorem is a method used to calculate the deflection or slope at a specific point in a structure by applying a virtual load or moment. The theorem is applicable to linearly elastic systems.

The two main equations are:

\[ y = \sum \frac{1}{EI} \int_0^L M_R \left( \frac{\partial M}{\partial P} \right) dx \quad \text{→ deflection} \]

\[ \theta = \sum \frac{1}{EI} \int_0^L M_R \left( \frac{\partial M}{\partial M'} \right) dx \quad \text{→ slope} \]

How to Use the Theorem:

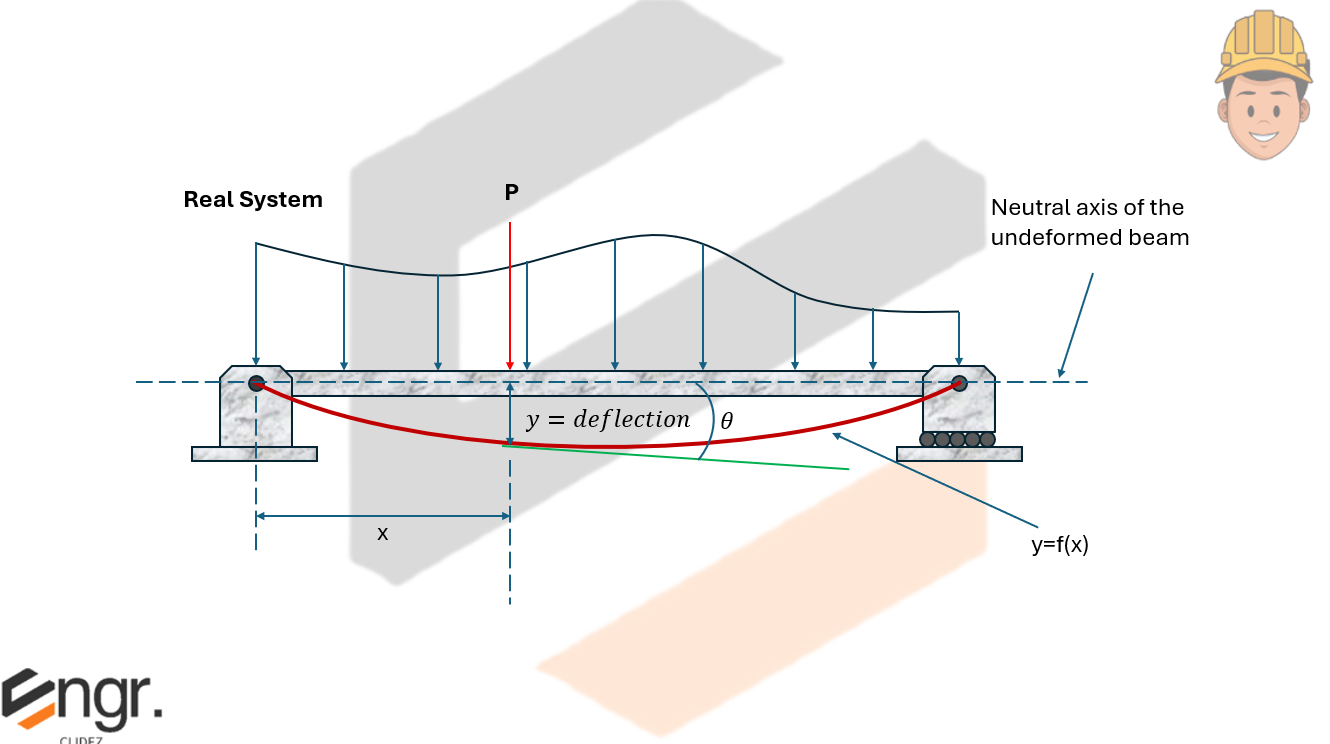
To find deflection at a point, apply a virtual load $P$ at that point.
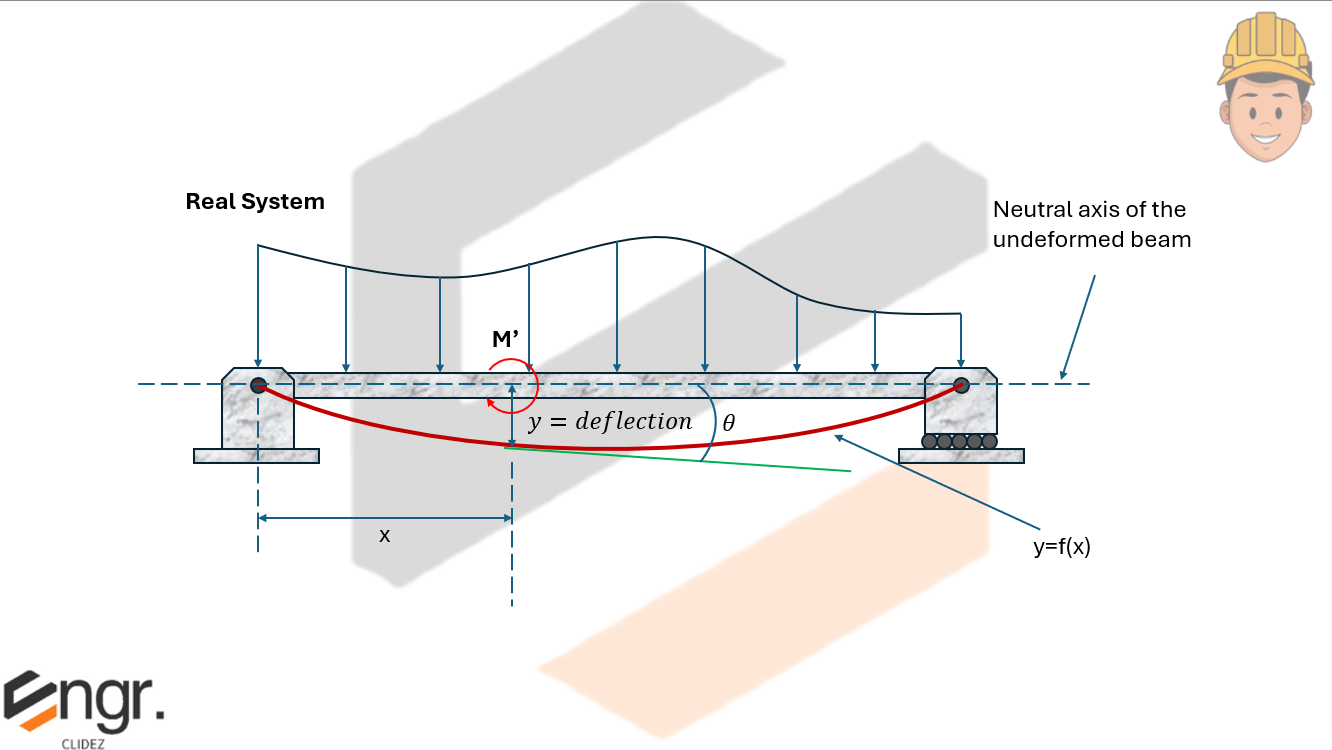
To find slope at a point, apply a virtual moment $M'$ at that point.

Segment-by-Segment Consideration:

You may integrate from left to right or right to left depending on your chosen origin.
If integrating from the left, include all loads to the left of the section.
If integrating from the right, include all loads to the right of the section.

Notes on Moment Expression:

$M$ refers to the bending moment expression including the virtual load or moment $P$ or $M'$.
Always verify your sign convention and assumption when setting up $M$:
- ⊕ Positive — correct assumption
- ⊖ Negative — wrong assumption

Understanding the Moment Expression in Castigliano’s Theorem

In Castigliano’s method, we work with the moment equation from the real beam, denoted as $M_R$. This excludes the virtual load $P$ or virtual moment $M'$, which are set to zero.

To compute deflection or slope, we use the following expressions:

$\frac{\partial M}{\partial P}$ — partial derivative of the moment $M$ with respect to virtual load $P$
$\frac{\partial M}{\partial M'}$ — partial derivative of $M$ with respect to virtual moment $M'$

Key Idea:

Differentiate the moment equation while treating everything else as a constant, except the term you're differentiating with respect to --> $P$ or $M'$.

Example 1: With respect to $P$

Given the moment equation:

\[ M = 7x^2 + 6Px + 8P + 5Px^2 \]

Differentiate with respect to $P$:

\[ \frac{\partial M}{\partial P} = 0 + 6x + 8 + 5x^2 = 6x + 8 + 5x^2 \]

Example 2: With respect to $M'$

Given the moment equation:

\[ M = 8x^3 + 7M'x^2 + 6M' + 29 \]

Differentiate with respect to $M'$:

\[ \frac{\partial M}{\partial M'} = 0 + 7x^2 + 6 + 0 = 7x^2 + 6 \]

This step-by-step differentiation allows us to substitute into Castigliano’s Theorem integrals to compute either deflection $\delta$ or slope $\theta$ at the point of interest.