CE Board Exam Randomizer

Area Moment Method

Consider 2 points A and B on the beam, as shown in the figure below:

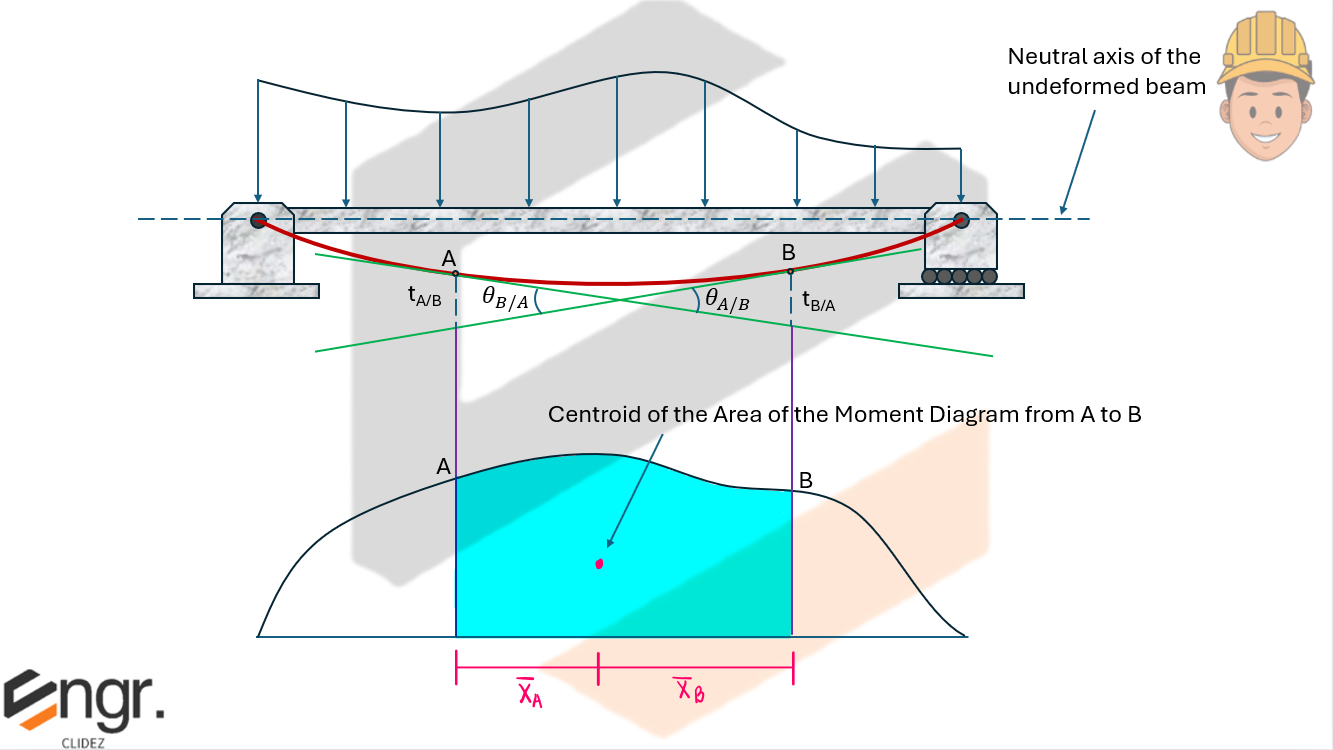
Theorem 1: The change in slope between the tangents drawn to the elastic curve at any 2 points A and B, $\theta_{BA}$, is equal to the product $1/EI$ multiplied by the area of the moment diagram between A and B. That is,

Theorem 2: The deviation of any point B relative to a tangent drawn to the elastic curve at any other point A, $t_{B/A}$, is equal to the product $1/EI$ multiplied by the moment of an area about B of that part of the moment diagram between points A and B. That is,

Sign Convention:
The rotation, $\theta$, is positive if counterclockwise from the left tangent and negative if clockwise from the left tangent. The deviation, $t$, is positive if the tangent is above the point, and negative if the tangent is below the point.

Moment Diagram by Parts

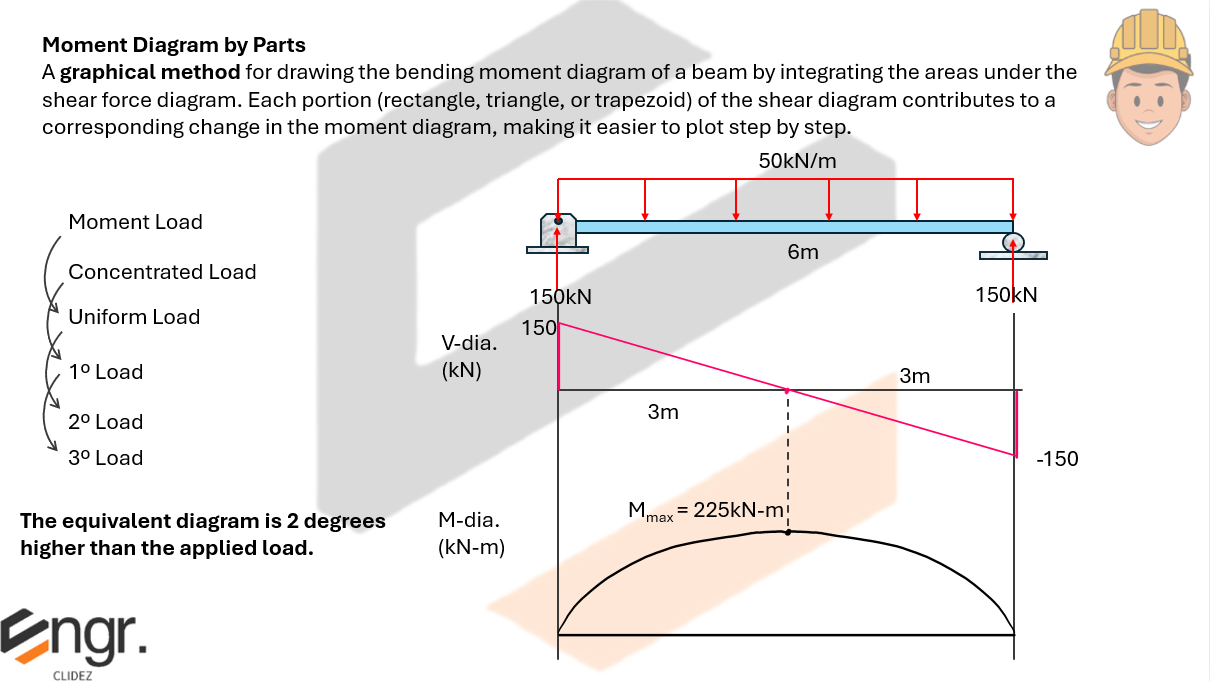
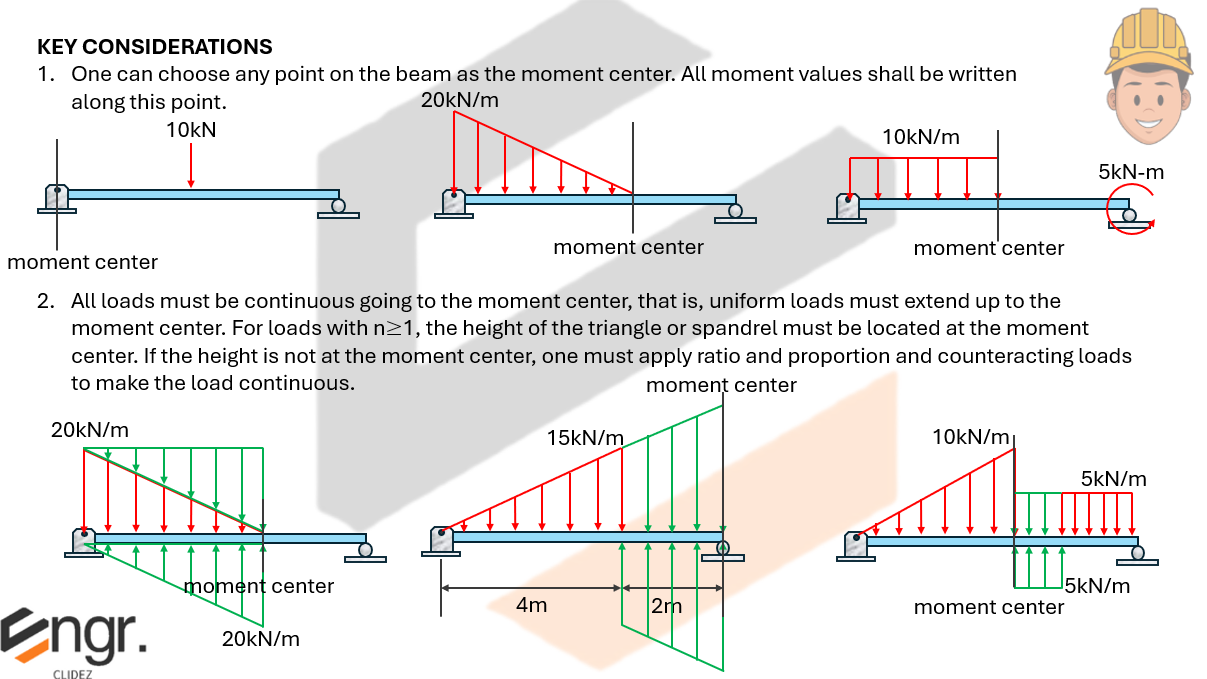
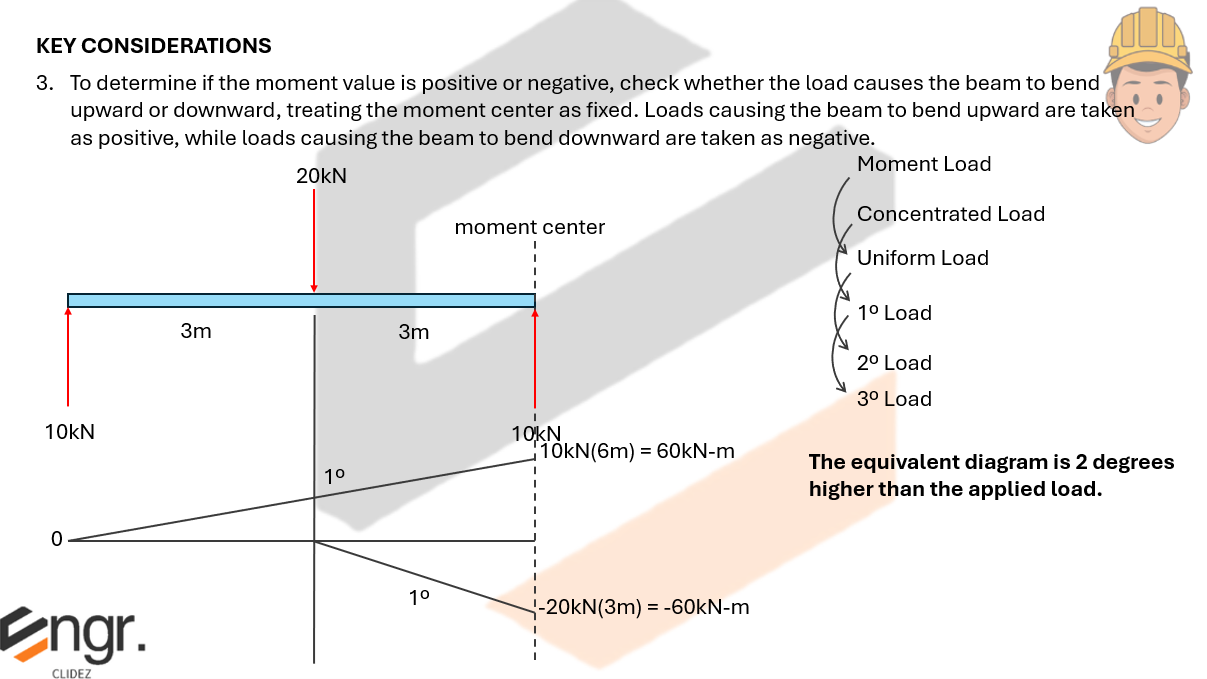
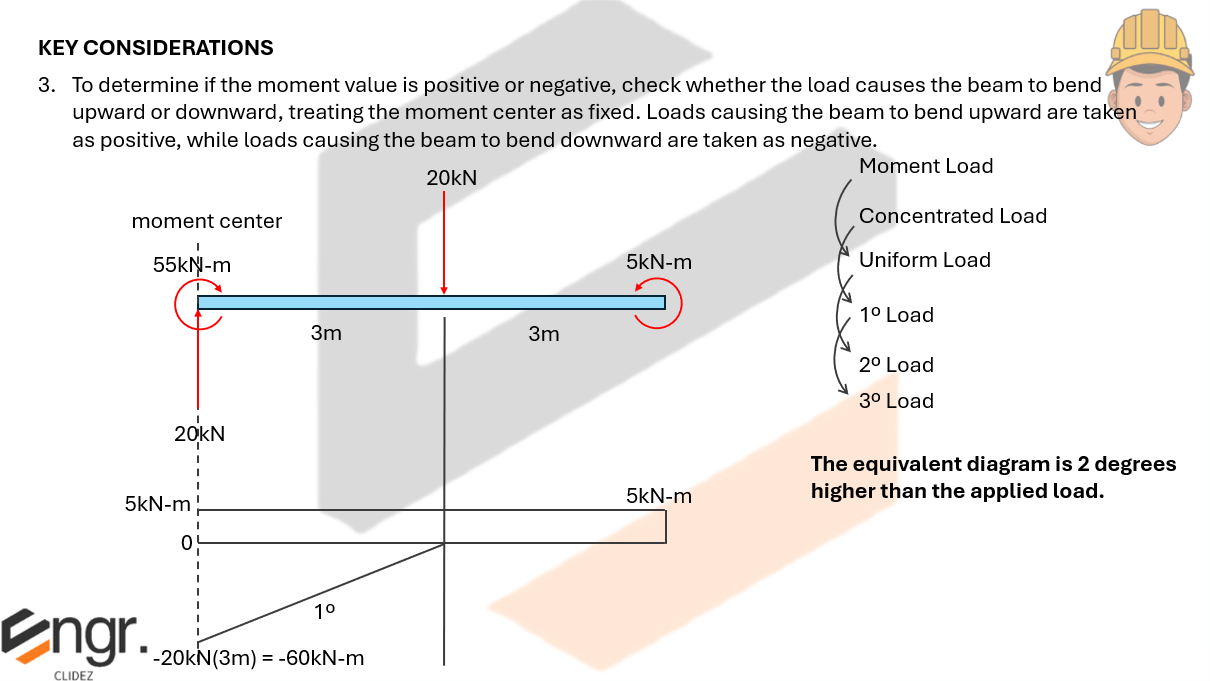
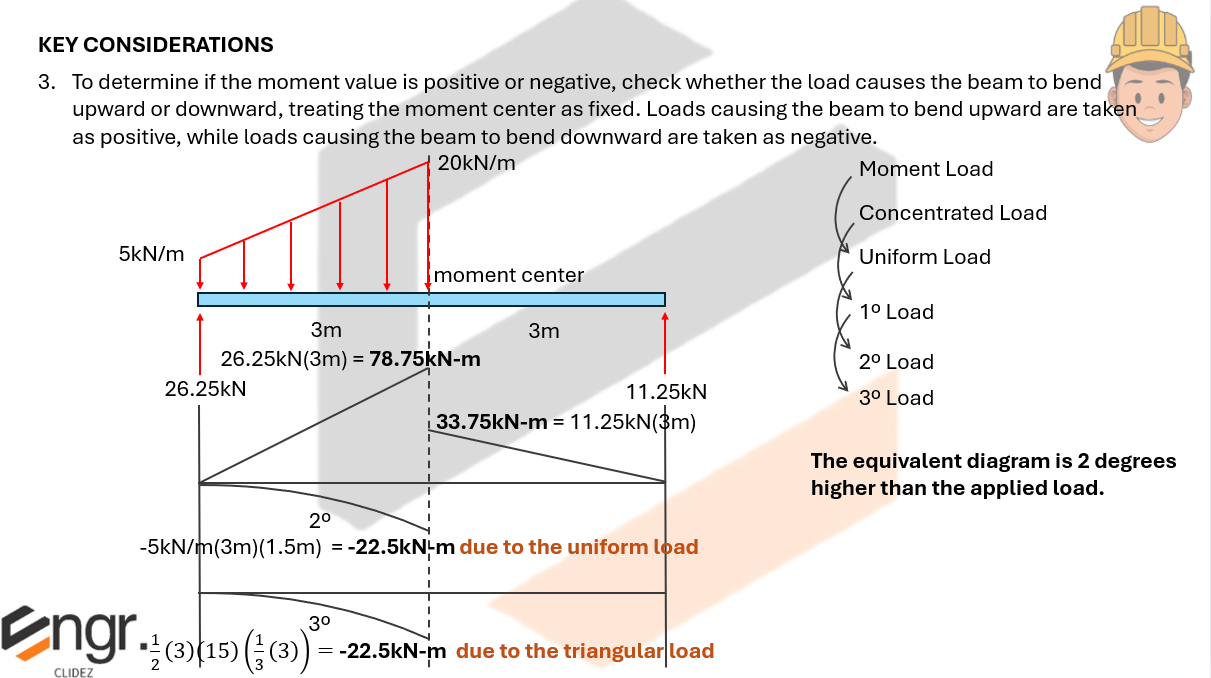
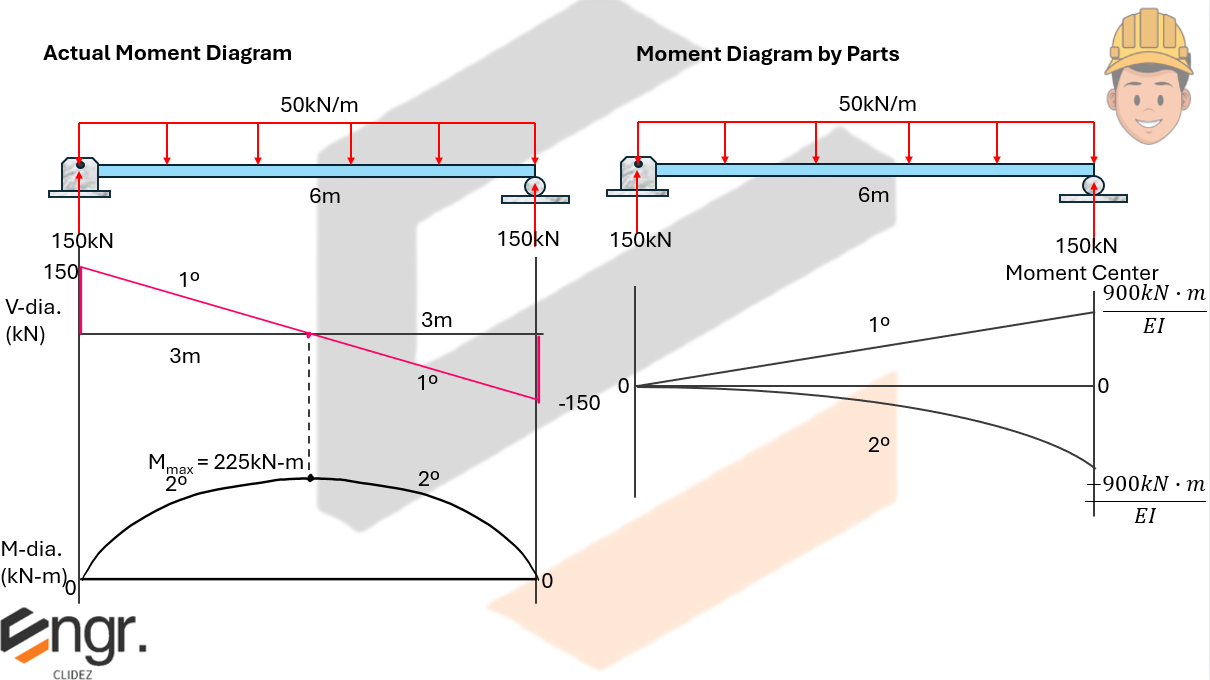
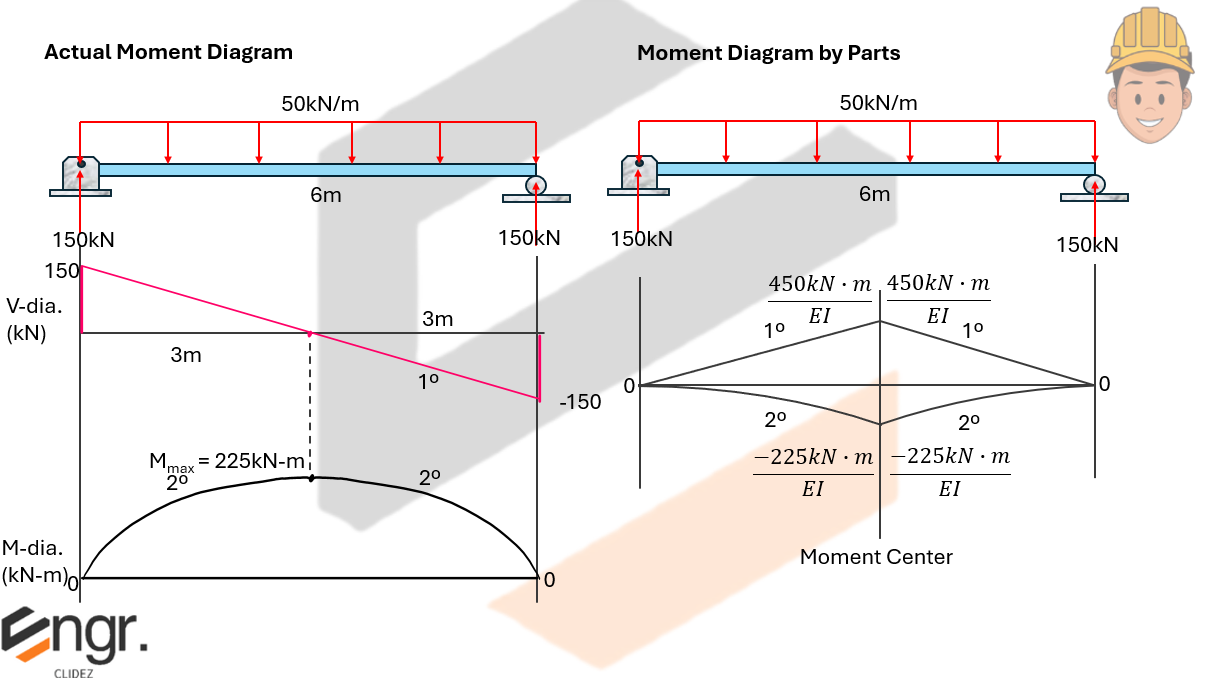
Here, we verify that the effect caused by the actual moment diagram and the moment diagram by parts are the same for the area and area-moment computations.

Problem 1:

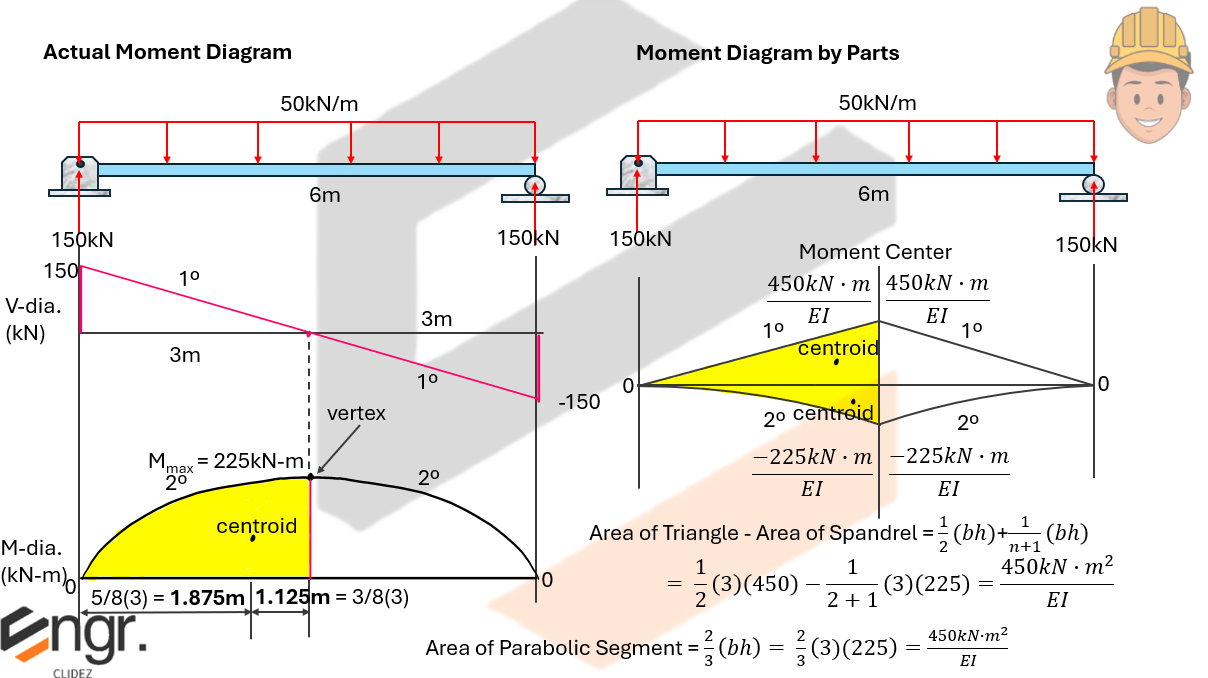
Using the Area Moment Method, determine the following:
a. The slope and deflection at 3m from the left end.
b. The deflection at the free ends, A and D.
c. The deflection and slope at the midspan.
d. The location and value of the maximum deflection between BC.

See images:

Problem 2:

Refer to the image shown:

See images:

Problem 3:

Refer to the image shown:

See images:

Problem 4:

Refer to the image shown:

See images:

Problem 5:

Refer to the image shown:

See images:

Problem 6:

Refer to the image shown:

See images:

Problem 7:

Refer to the image shown:

See images:

Problem 8:

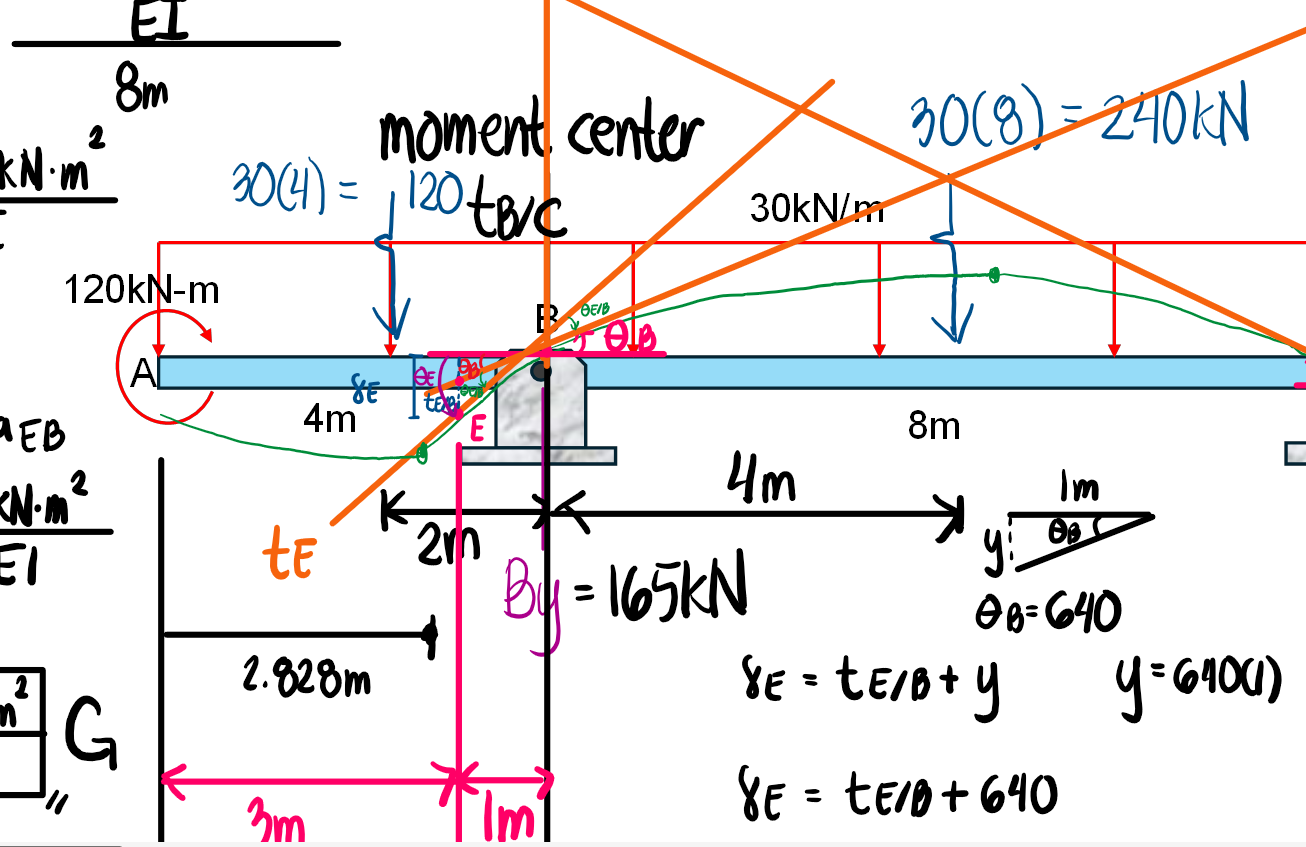
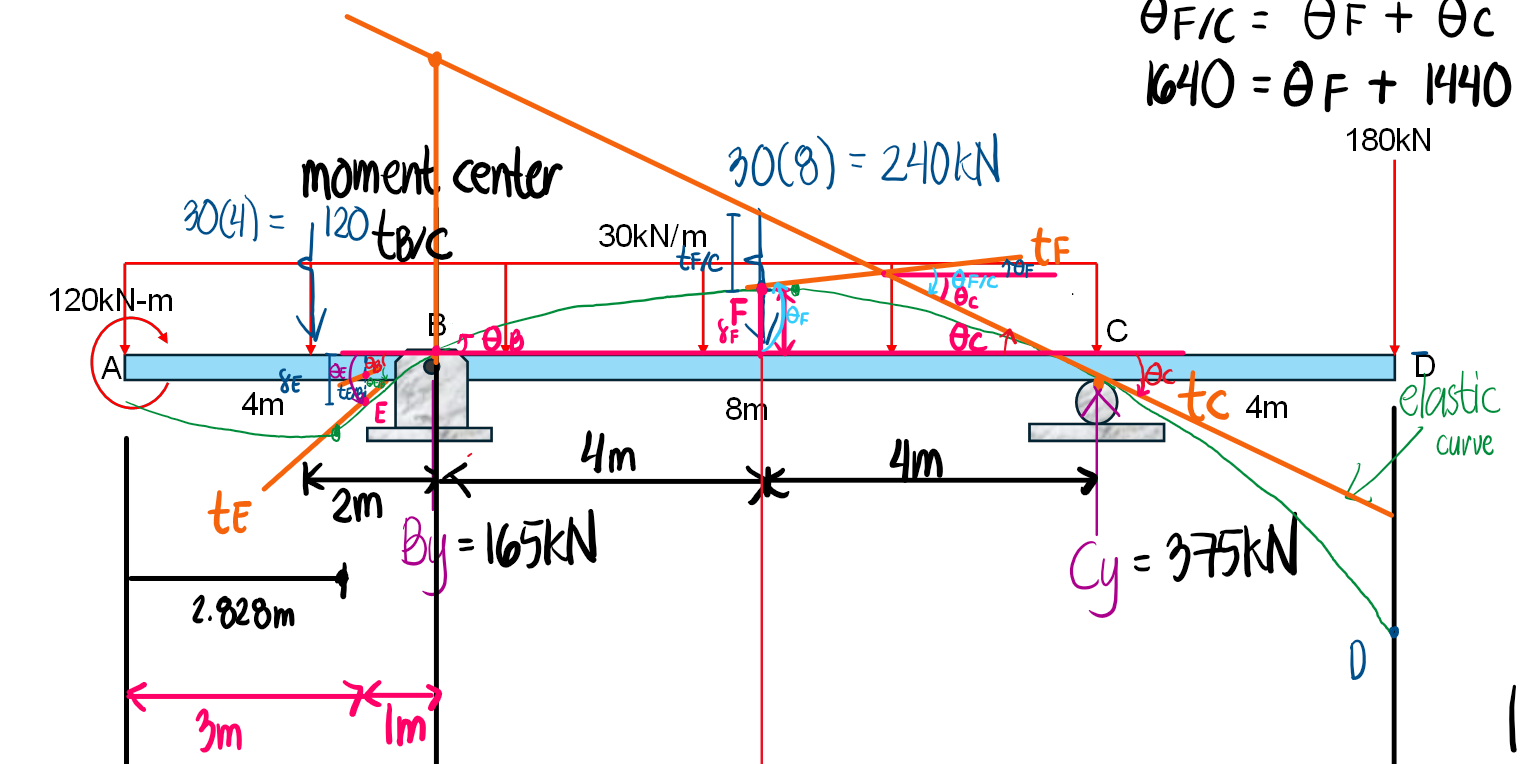
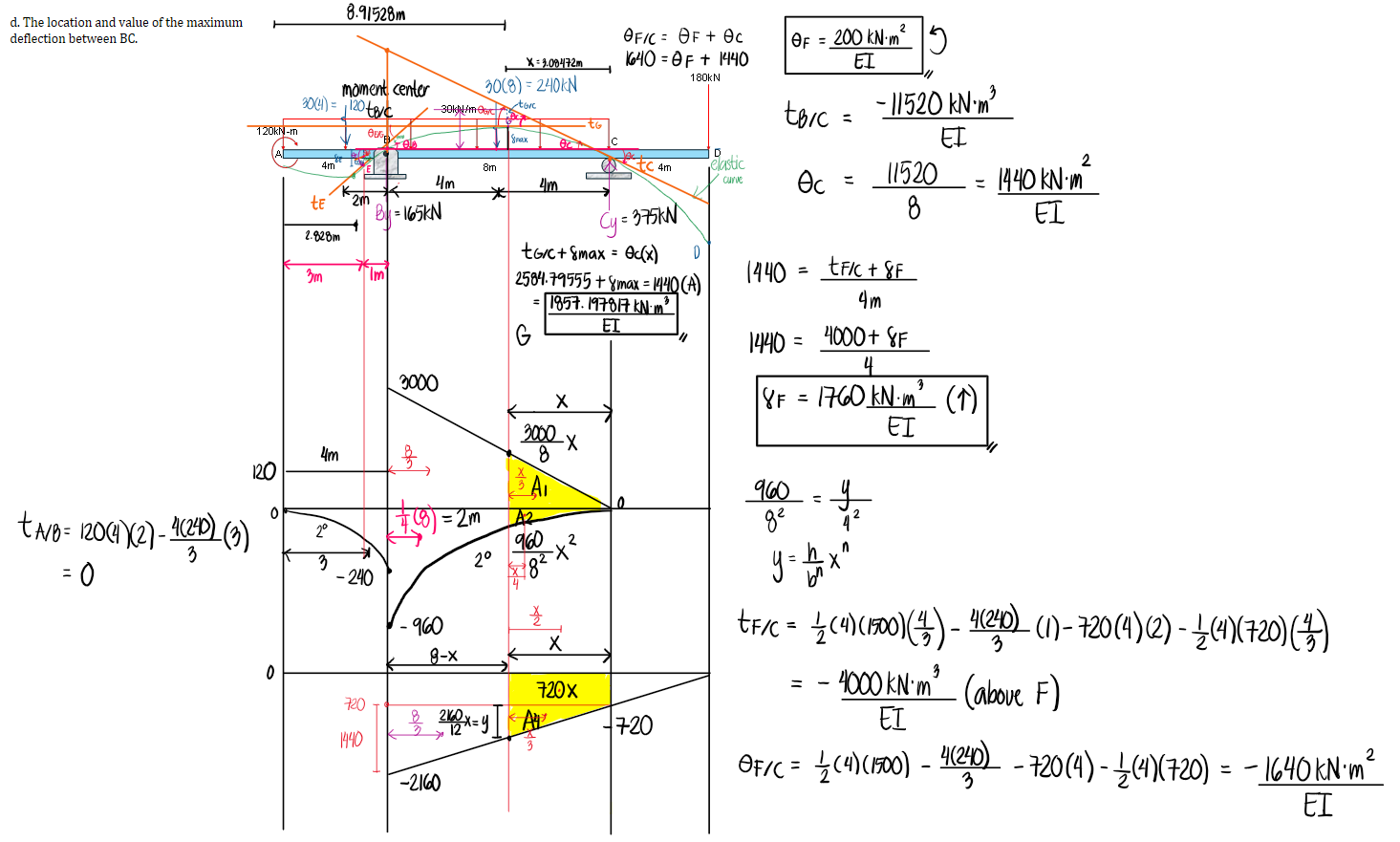
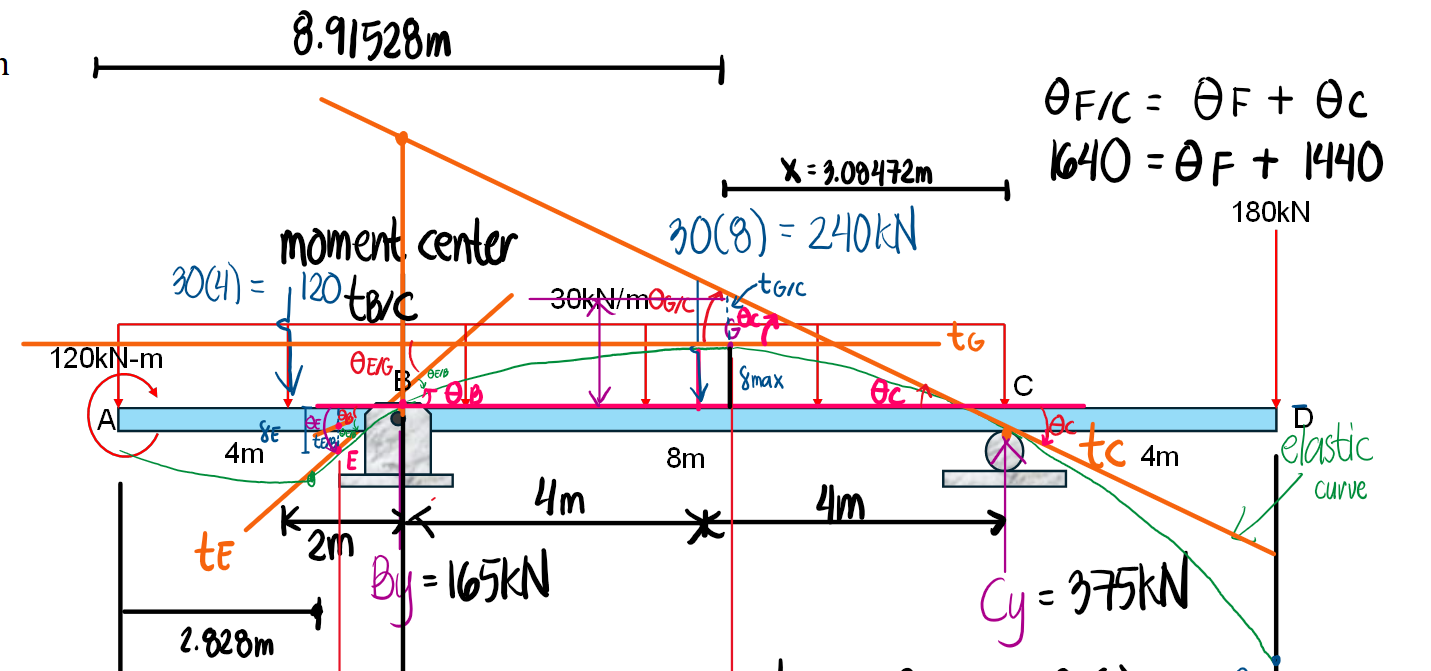
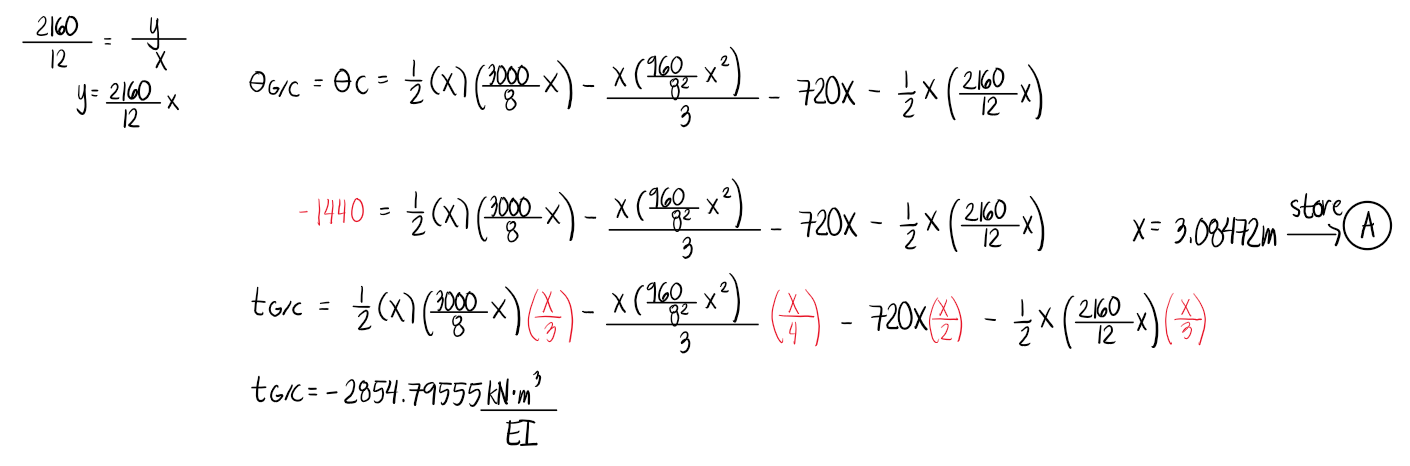
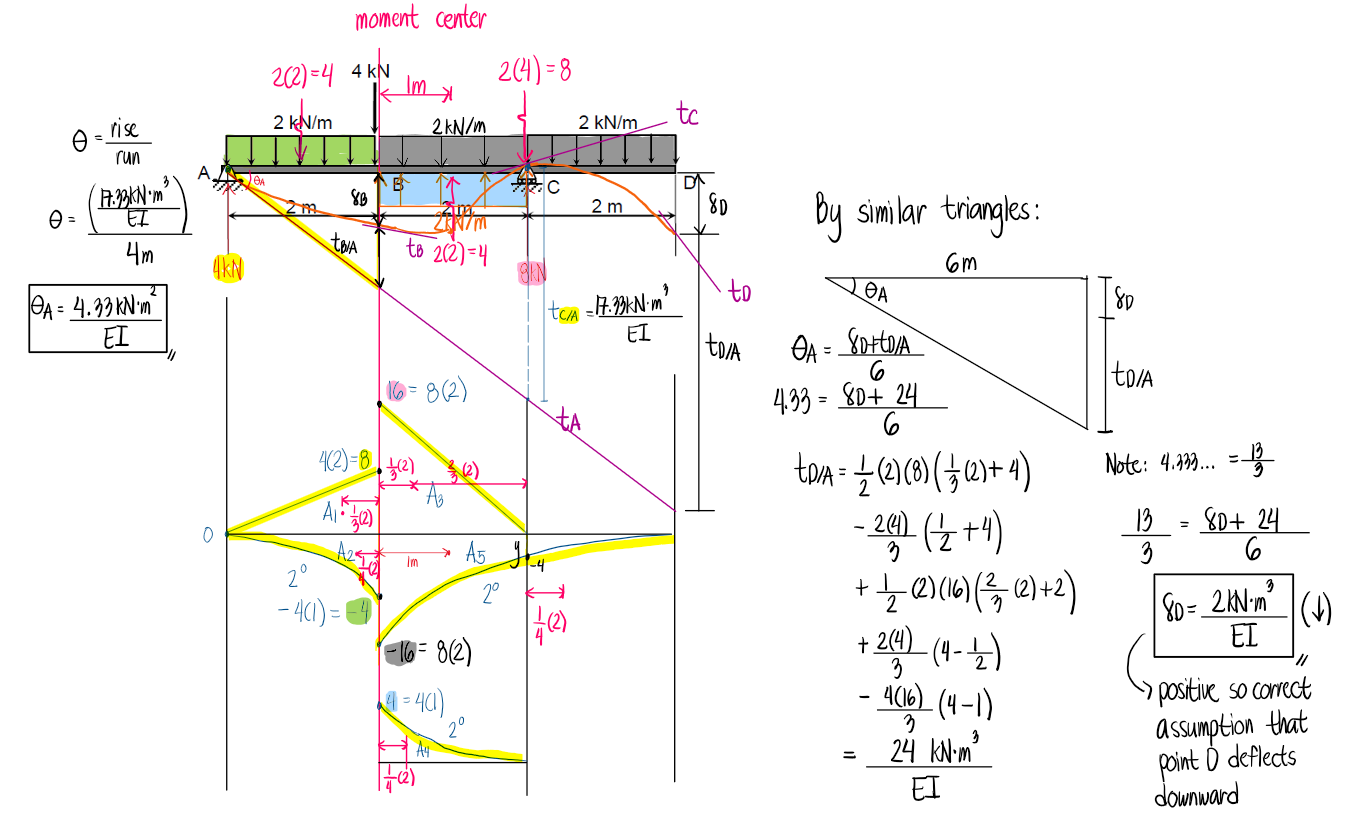
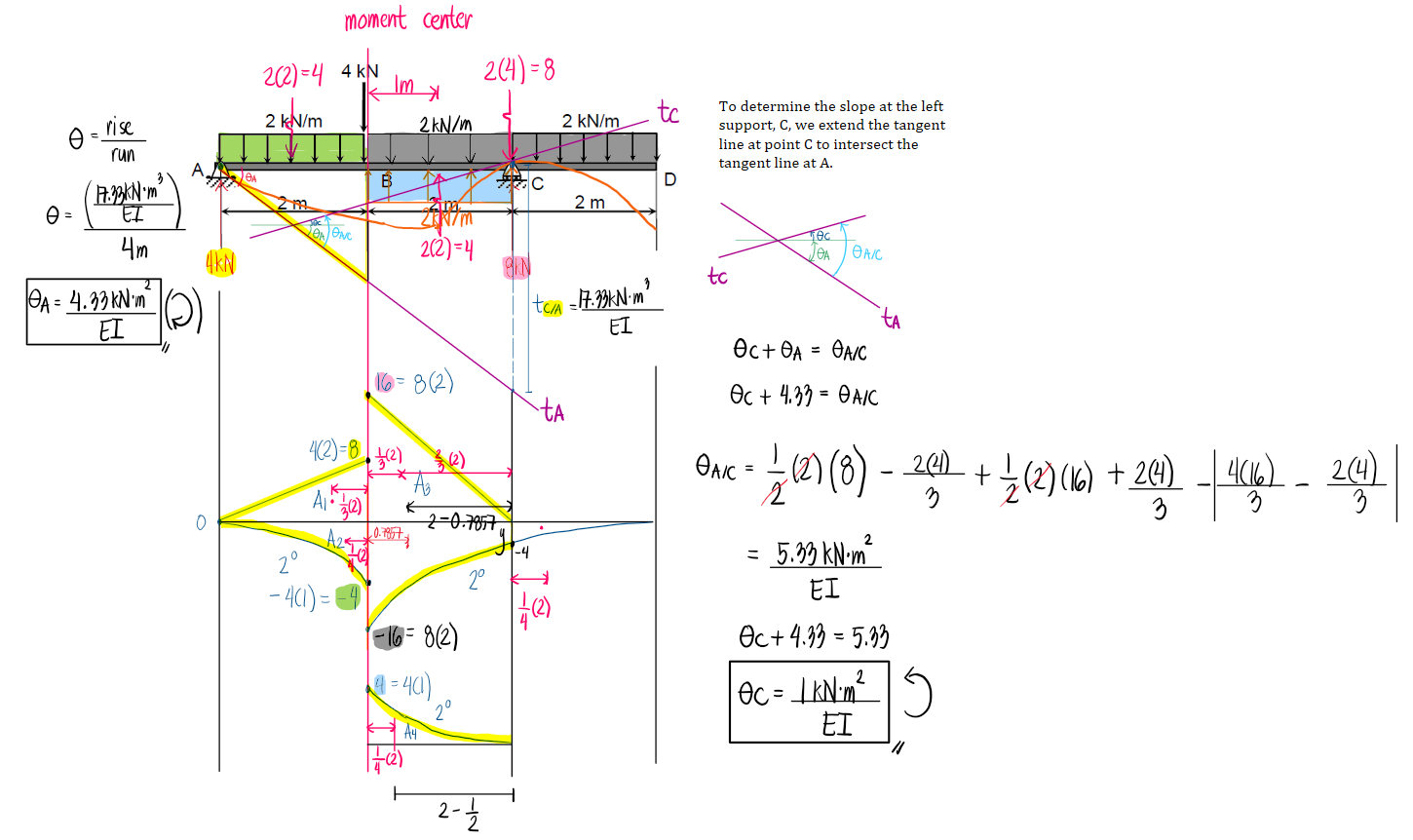
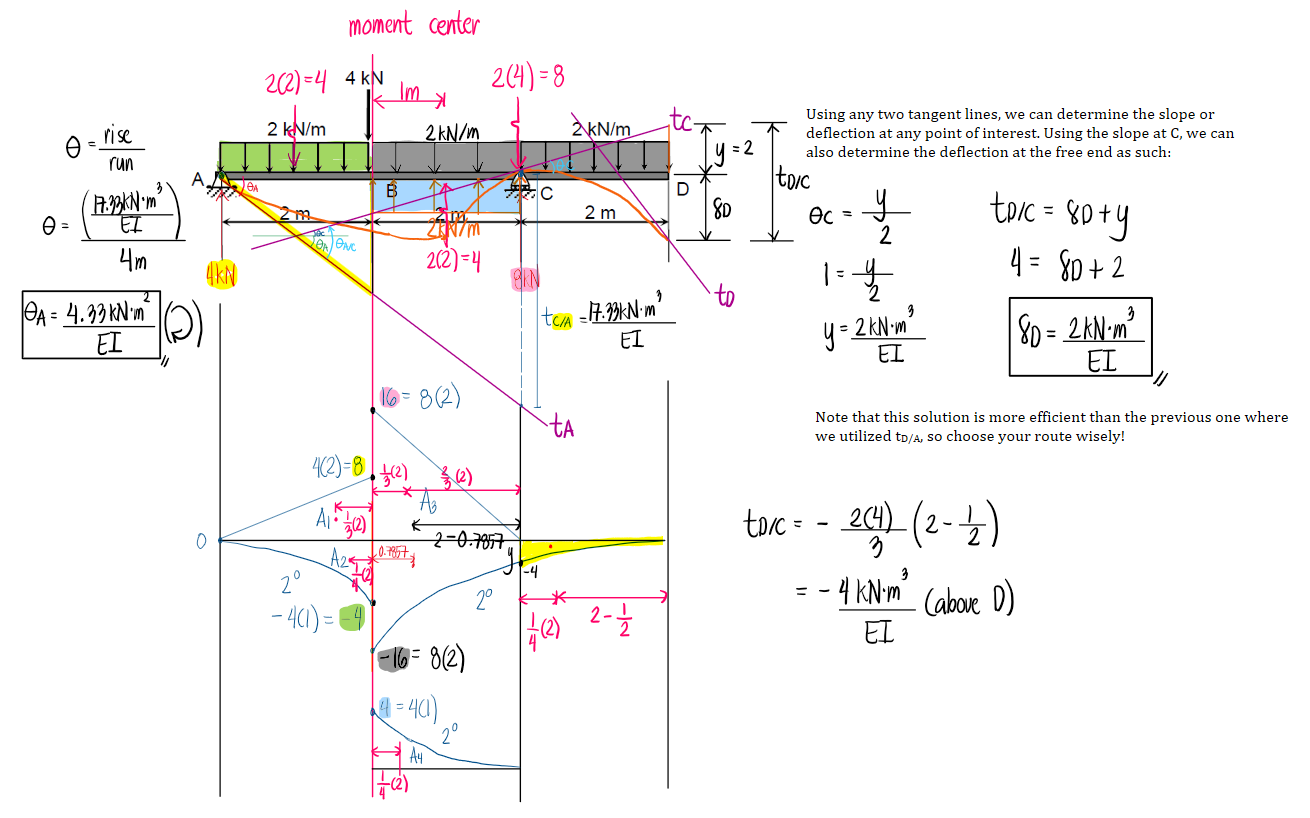
Refer to the image shown:

See images: