Moment of Inertia

Problem 1:

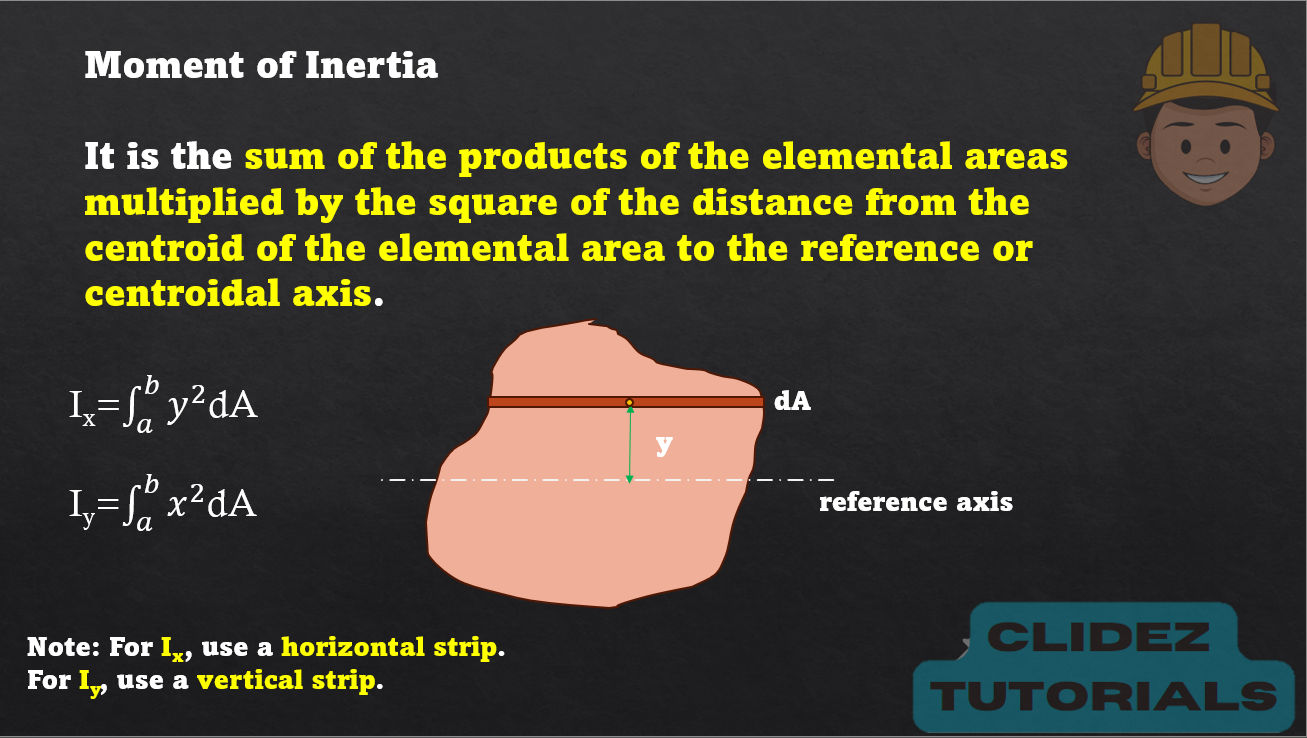
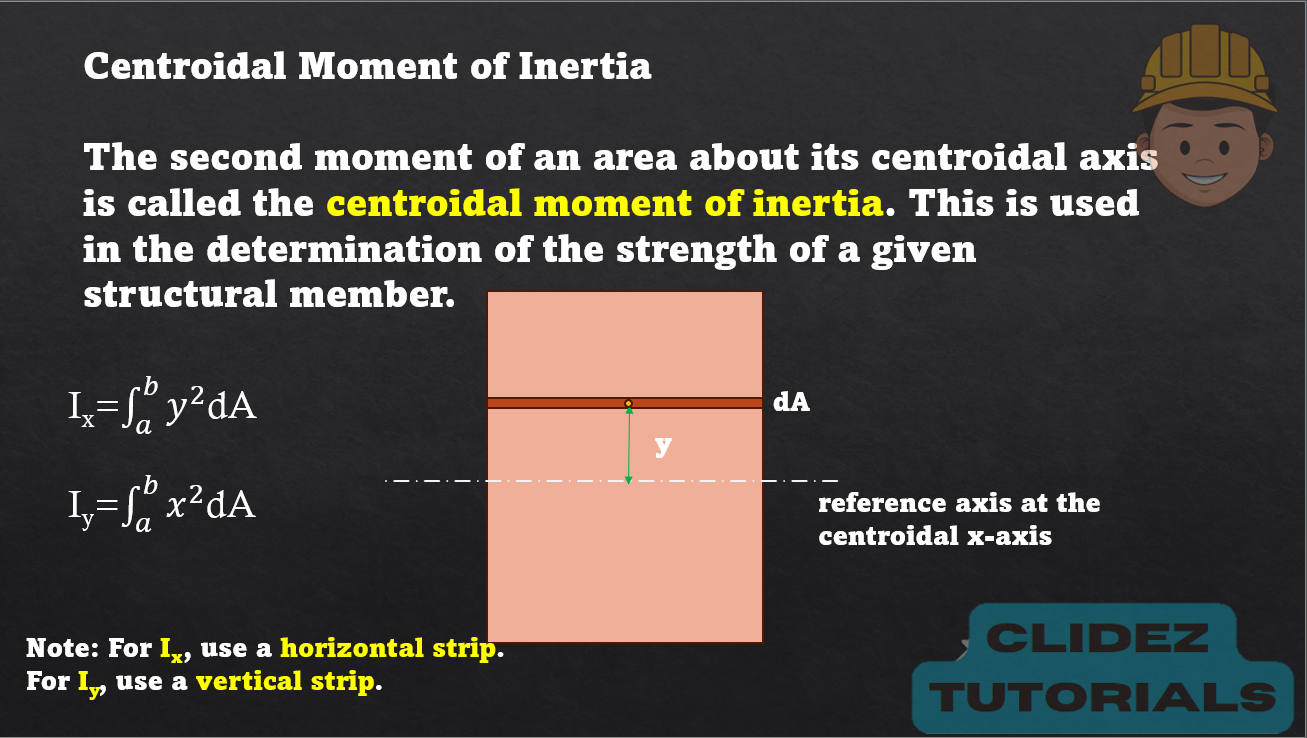
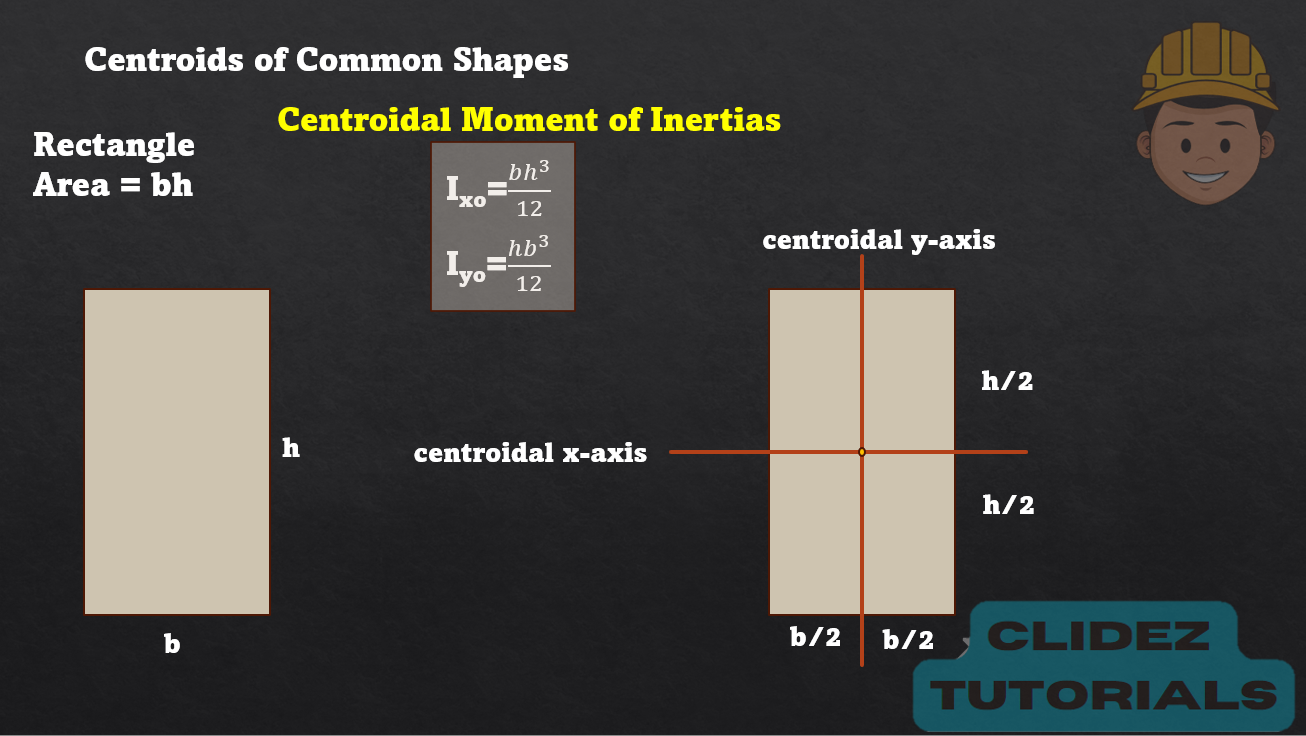
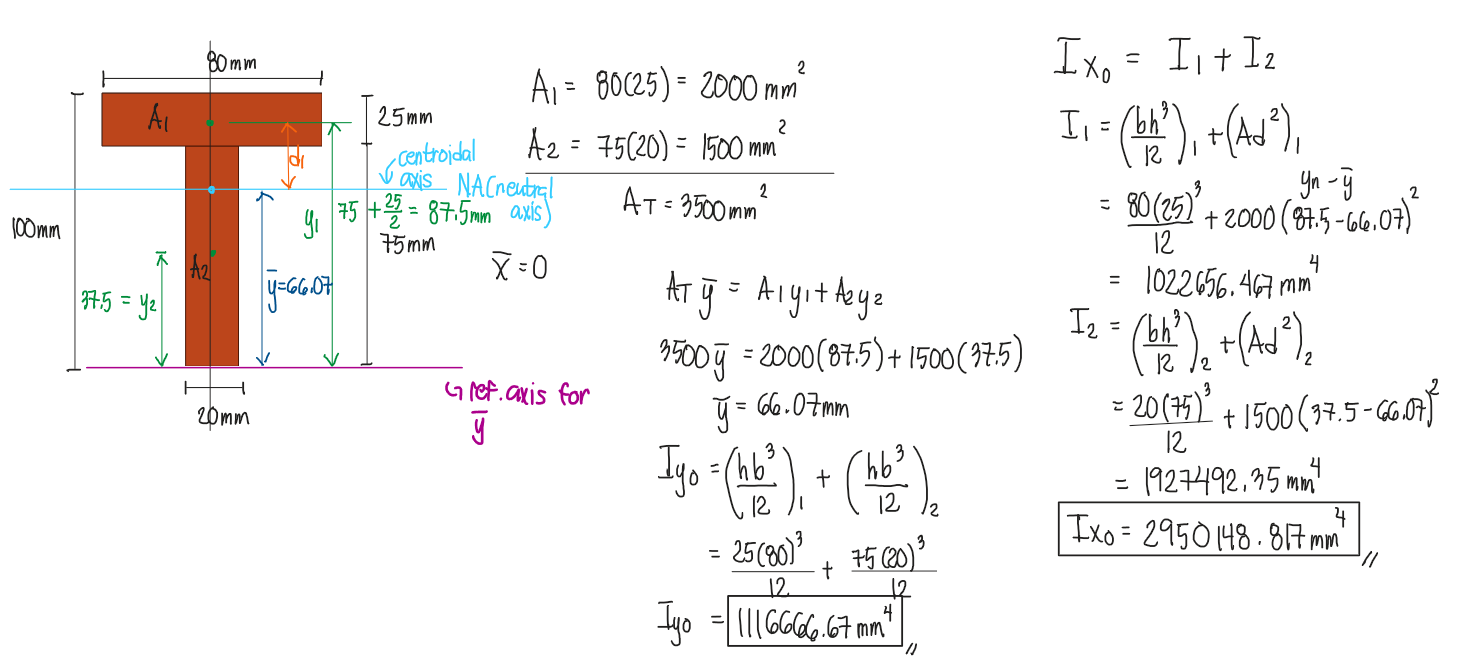
For the given figure, locate the centroid and solve the moment of inertia about the centroidal axes.

The figure below has a vertical axis of symmetry, meaning that the centroidal y-axis is located along this axis. Therefore, we don't have to apply the transfer formula for the moment of inertia about the y-axis and we simply add the individual I_yo of each shape. However, the centroidal x-axes of each shape does not coincide with the centroidal x-axis of the total shape. Thus, we need to apply the transfer formula, Ad², to transfer the centroidal moment of inertia of each shape to the centroid of the total figure.

Problem 2:

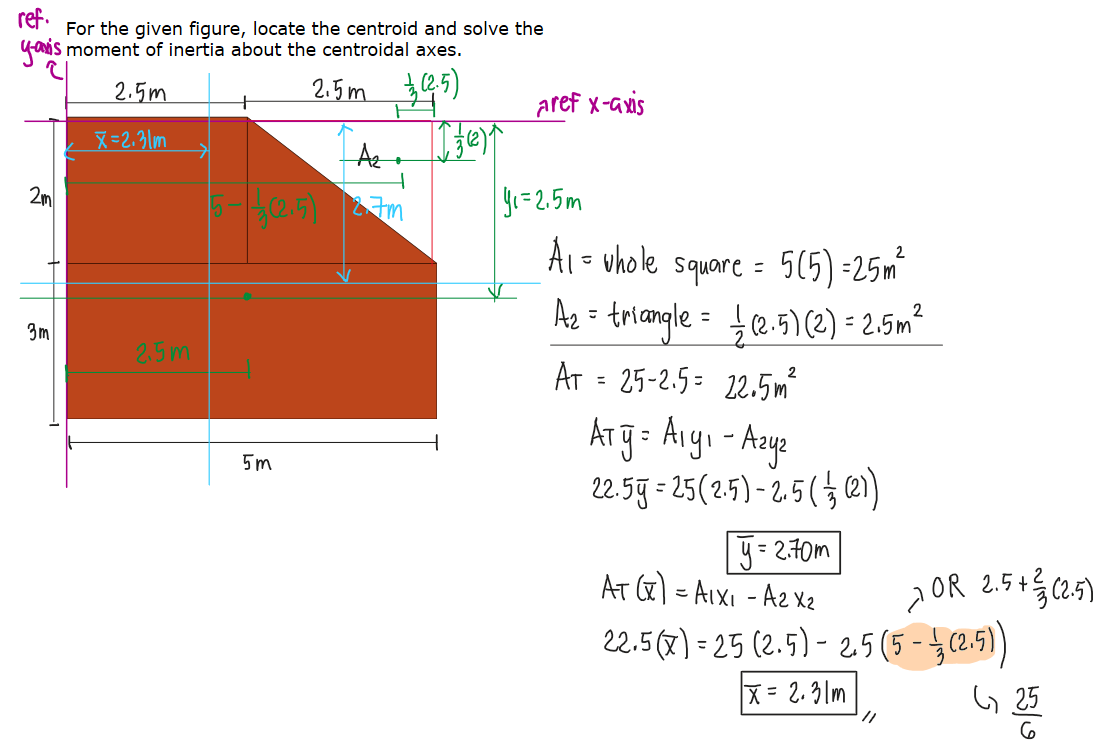
For the given figure, locate the centroid and solve the moment of inertia about the centroidal axes.

See images:

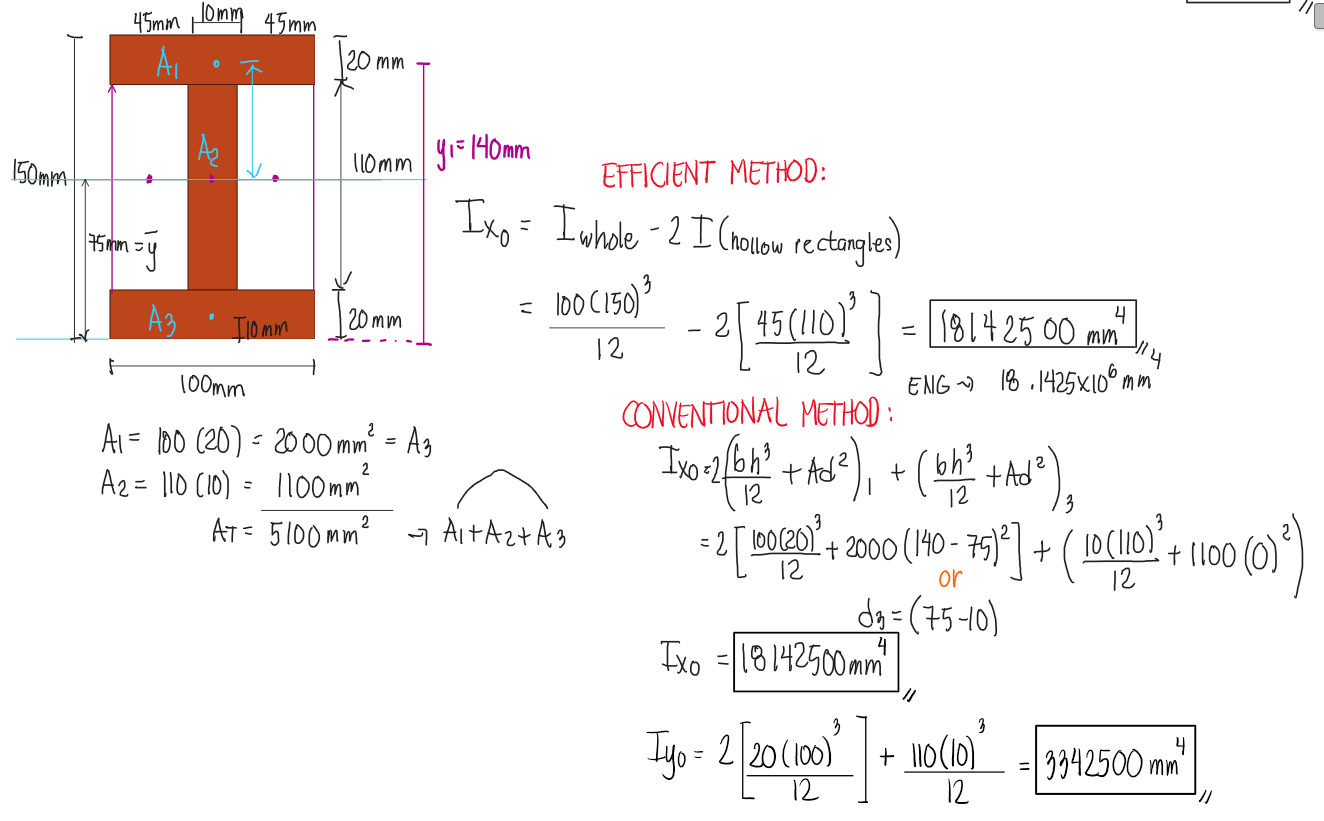
We applied the same method used in the previous chapter for finding centroids, where hollow sections are subtracted. Similarly, to determine the total centroidal moment of inertia, we must also use subtraction—specifically, by subtracting the transformed centroidal moment of inertia of the hollow section from that of the larger solid section.

Problem 3:

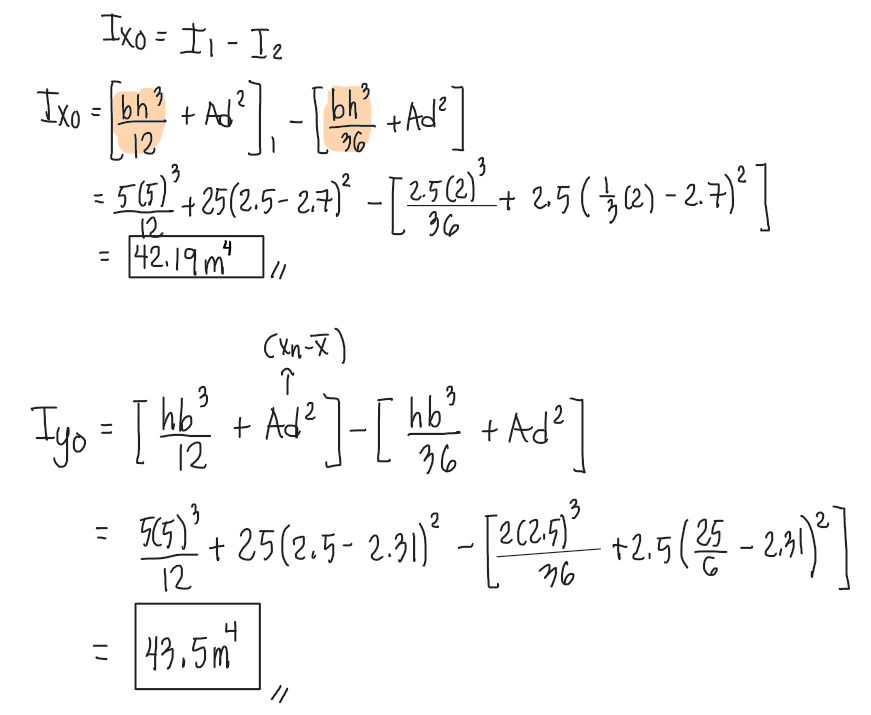
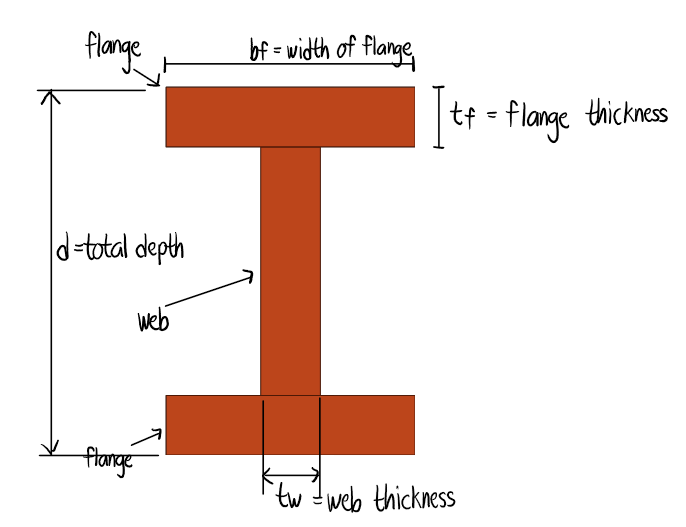
A wide flange section has the following dimensions: Flange thickness = 20mm
Flange width = 100mm
Total depth = 150mm
Web thickness = 10mm

See images:

Problem 4:

For the given figure, locate the centroid and solve the moment of inertia about the centroidal axes.

Since the figure has a vertical and horizontal axis of symmetry, the centroid is immediately located at the geometric center.

Then, by symmetry: I_xo=I_yo
I_xo = I_yo = I_square - I_circle=$\frac{bh^3}{12} - \frac{\pi D^4}{64}$ $$ \frac{3\cdot3^3}{12} - \frac{\pi\cdot2^4}{64}=5.96m^4 $$ Solution

Problem 5:

Refer to the image shown:

See images:

Problem 6:

Refer to the image shown:

See images:

Problem 7:

Refer to the image shown:

See images:

Problem 8:

Refer to the image shown:

See images: