Forces in Space (3D Systems) | Statics of Rigid Bodies

Forces in Space

In the previous chapter, we focused our discussion on coplanar force systems&—that is, forces in two dimensions. In this chapter, we extend our discussion to forces in three dimensions.

The figure below shows a force F in a three-dimensional system. The components of the force are proportional to the components of its distance from tail to head. In equation form, it is expressed as:

$$ \frac{F_x}{F} = \frac{x}{L} \quad \text{(1)} $$

$$ \frac{F_y}{F} = \frac{y}{L} \quad \text{(2)} $$

$$ \frac{F_z}{F} = \frac{z}{L} \quad \text{(3)} $$

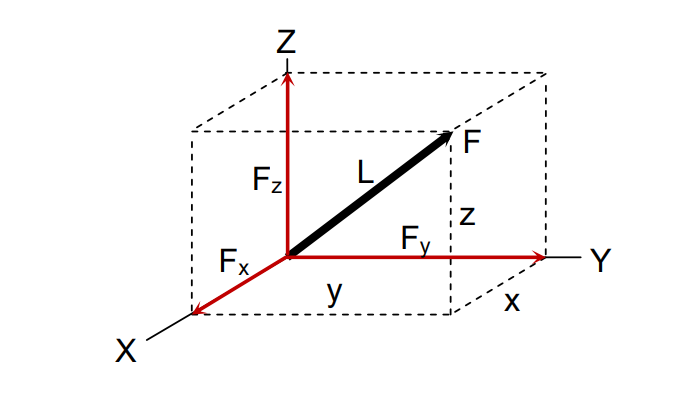
Example 1: A force F = 340 kN has its tail at the origin and its head at the point (3, 5, 7).

Distance from Tail to Head:

$$ L = \sqrt{x^2 + y^2 + z^2} = \sqrt{3^2 + 5^2 + 7^2} = 9.11 $$

Component Calculations:

$$ F_x = \frac{3}{9.11} \cdot 340 = 111.96 \text{ kN} $$

$$ F_y = \frac{5}{9.11} \cdot 340 = 186.61 \text{ kN} $$

$$ F_z = \frac{7}{9.11} \cdot 340 = 261.25 \text{ kN} $$

Sign Convention:

Proper sign convention should be considered. Oppositely directed forces have opposite signs. The right-handed sign convention is commonly used:

+X: Toward the reader; −X: Away
+Y: Right; −Y: Left
+Z: Upward; −Z: Downward

Moment of a Force in Three-Dimensional System

We define a moment as the product of the magnitude of the force and the perpendicular distance from the line of action of the force to the point:

$$ M = F \cdot d $$

where $ d $ is the moment arm, the perpendicular distance.

The principle of moments still applies in three-dimensional force systems, and is expressed as:

$$ M_A = \sum \left( \mathbf{F} \times \mathbf{d} \right) $$