CE Board Exam Randomizer

⬅ Back to Subject Topics

Equilibrium of Non-concurrent Force Systems

  1. Translational Equilibrium: The sum of all external forces in every direction must be zero
$$\sum F_x = 0,\quad \sum F_y = 0,\quad \sum F_z = 0 \quad \text{(for 3D systems)}$$
  1. Rotational Equilibrium: The sum of all moments about any point must also be zero
$$\sum M = 0$$

In engineering mechanics, a non-concurrent force system refers to a group of forces whose lines of action do not intersect at a single point. These forces may act on different parts of a rigid body and can include forces and moments (torques). To achieve equilibrium in such systems, a body must satisfy both conditions above.


    General Resultant of Non-concurrent Force Systems:
$$R = \sqrt{(\sum F_x)^2 + (\sum F_y)^2 + (\sum F_z)^2}$$


    For Forces Lying on a 2D Plane Only
$$\tan(\theta) = \frac{\sum F_y}{\sum F_x}$$
    Directional Cosines:
\(\cos(\theta_x) = \frac{F_x}{F}\)

\(\cos(\theta_y) = \frac{F_y}{F}\)

\(\cos(\theta_z) = \frac{F_z}{F}\)
    The location of the resultant force is determined by Varignon's Theorem.
$$ R(d_x) = F_1(x_1) + F_2(x_2) + \cdots + F_n(x_n) $$ $$ R(d_y) = F_1(y_1) + F_2(y_2) + \cdots + F_n(y_n) $$
Concept Concept Concept Concept Concept Concept Concept Concept Concept

Problem 1:

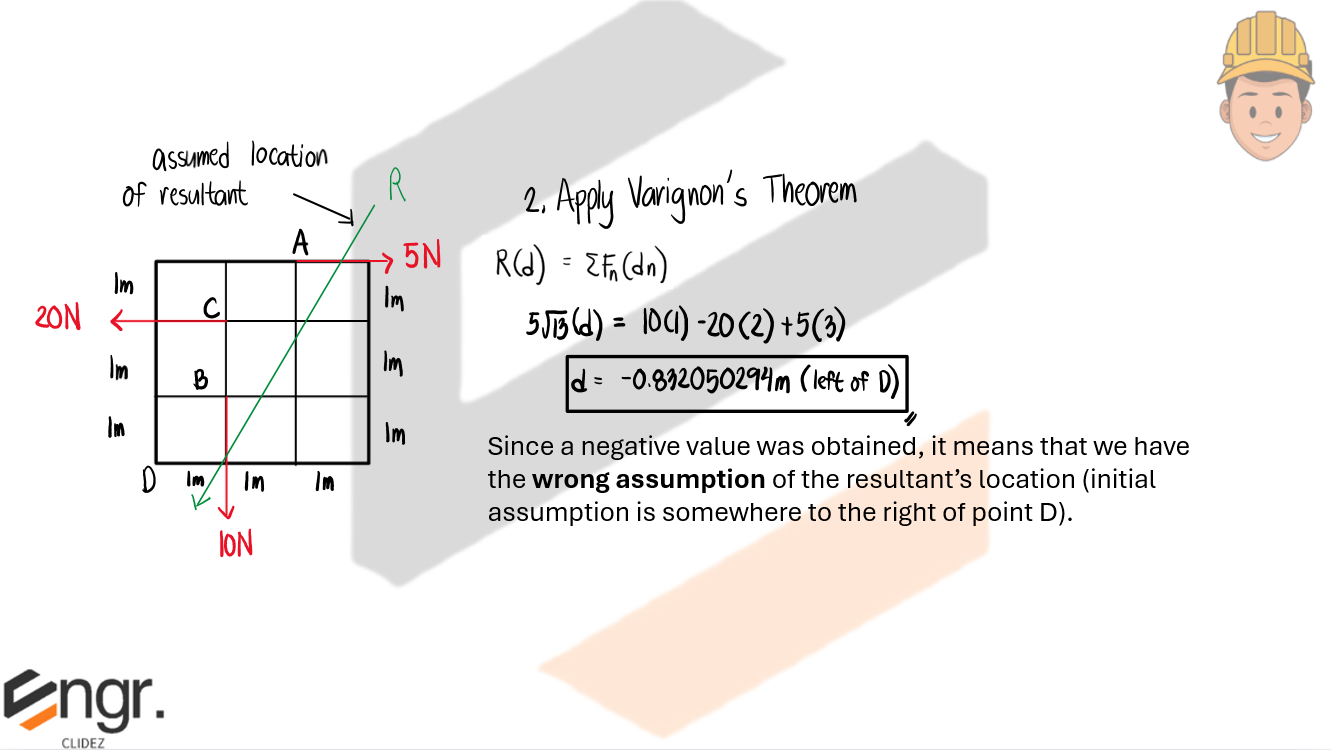
a. Calculate the location of the resultant from point D.
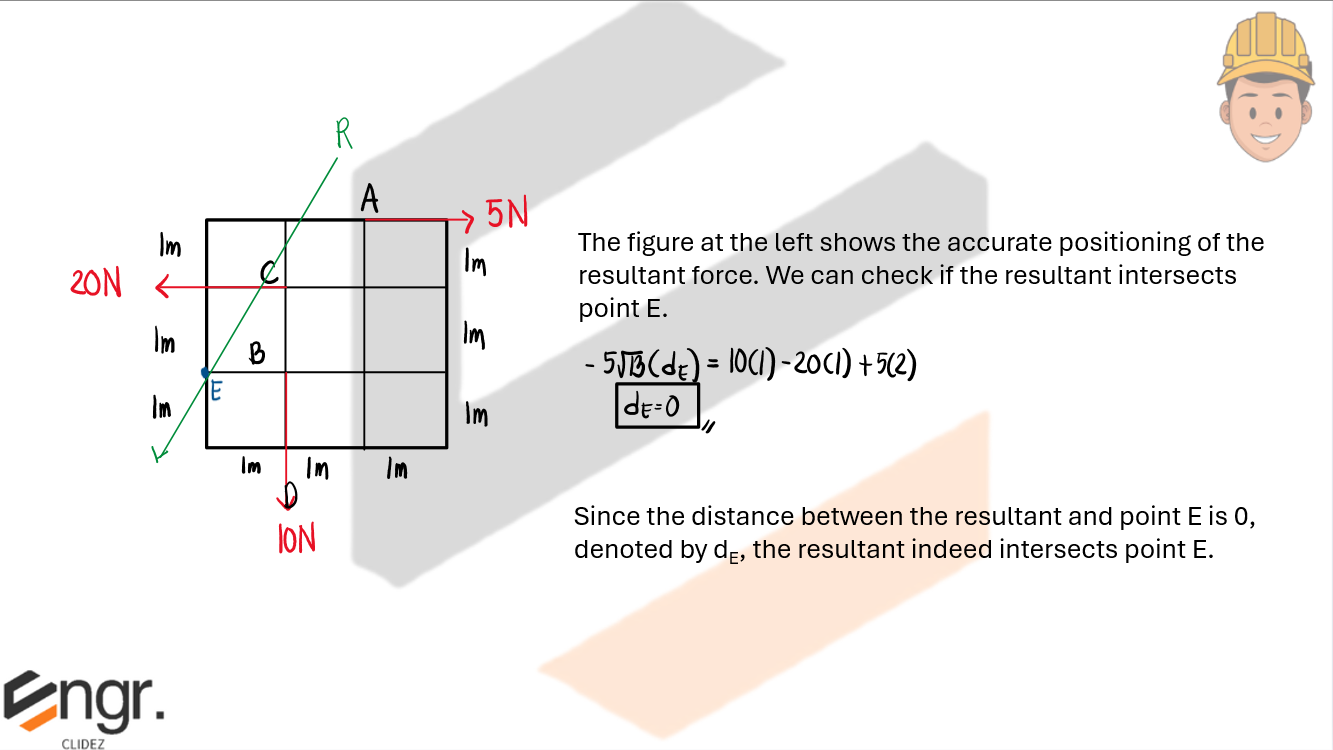
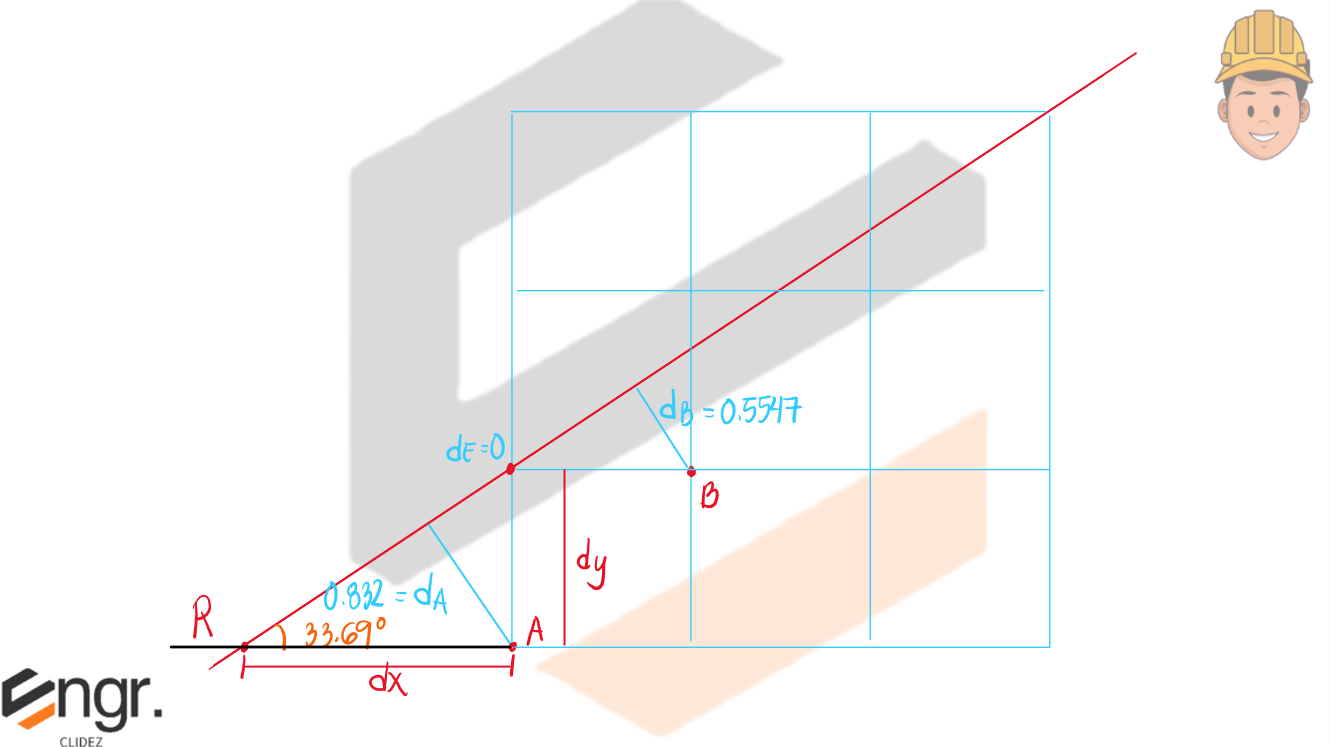
b. Prove that the resultant force intersects point E (as indicated below)
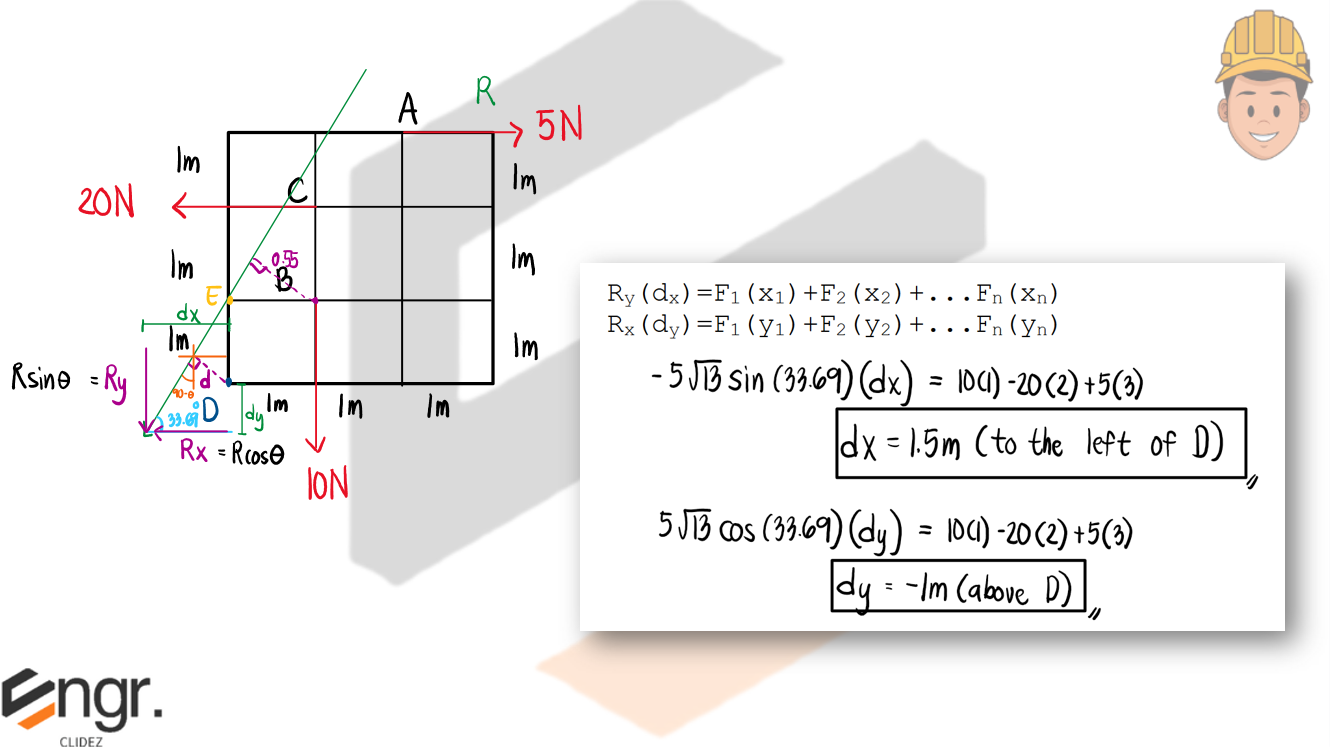
c. Determine the distance dx and dy from point D to the resultant force and indicate the location relative to D.
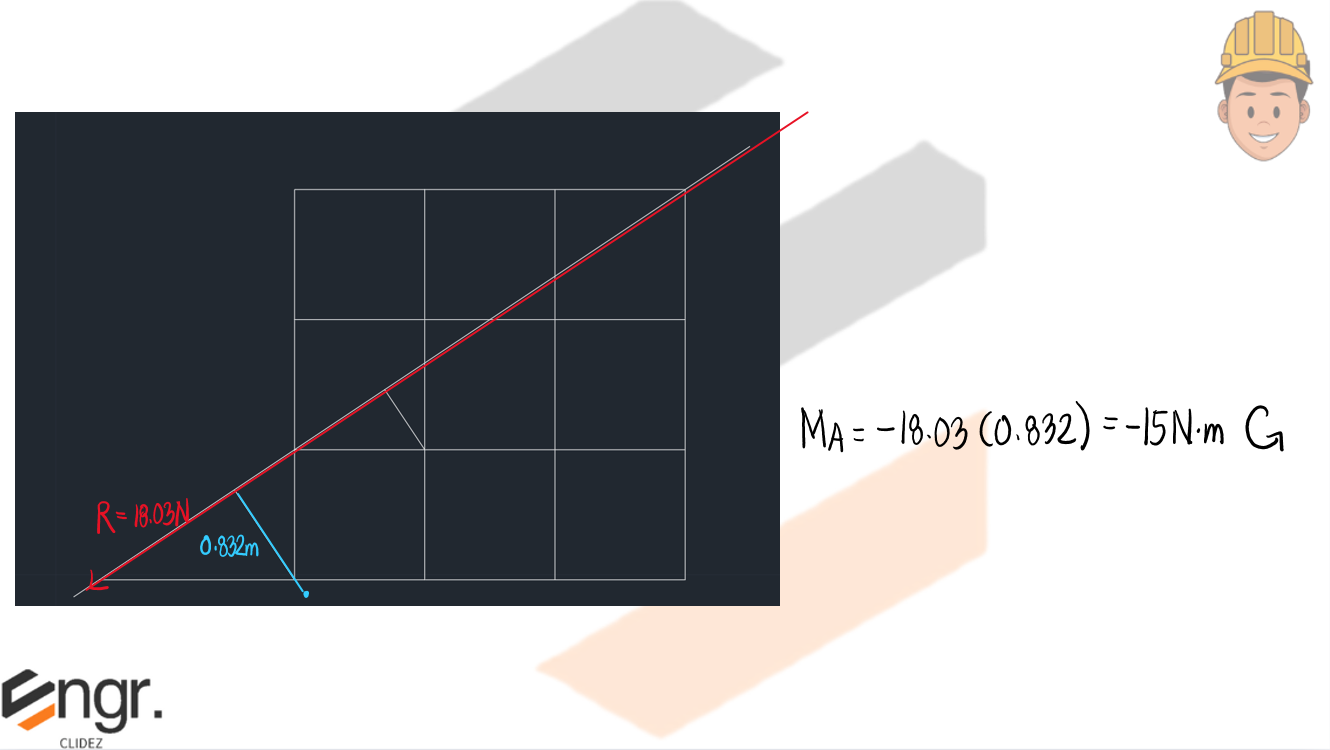
d. Determine the distance from point B to the resultant force.
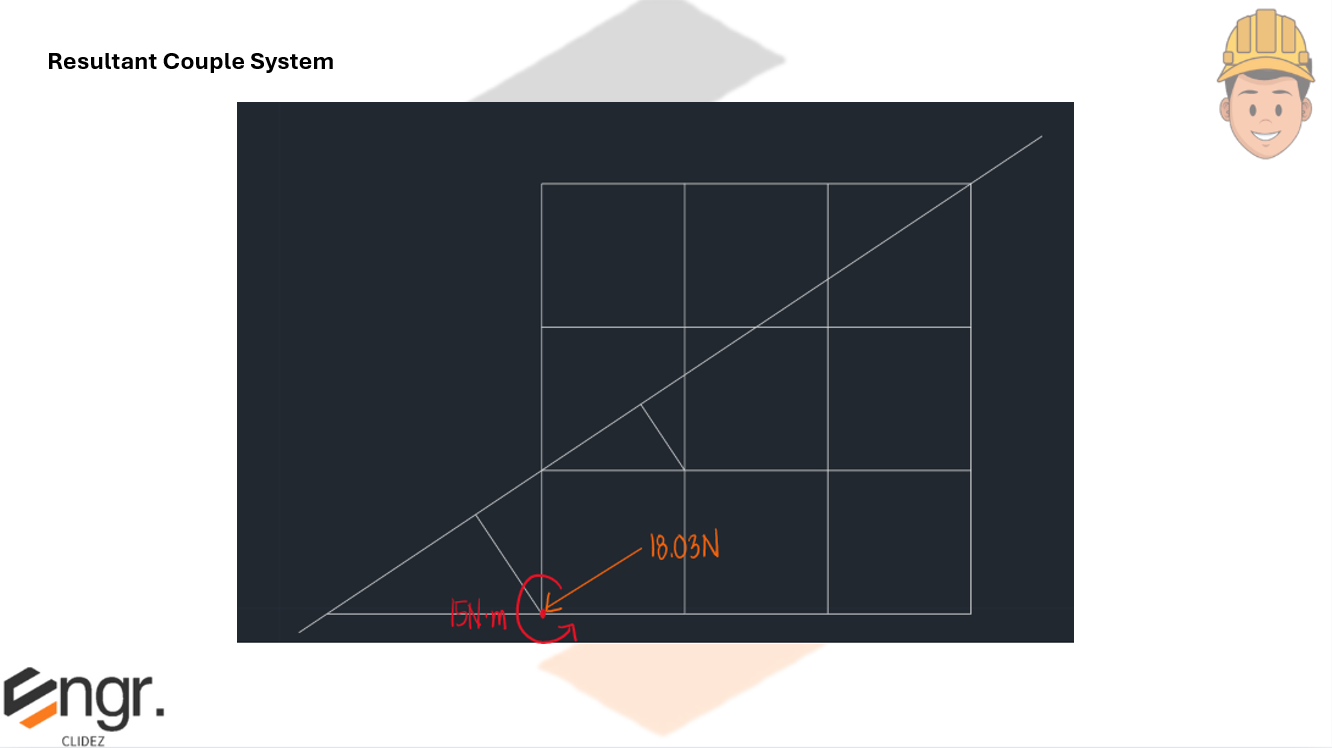
e. Resolve the system into a resultant-couple system.

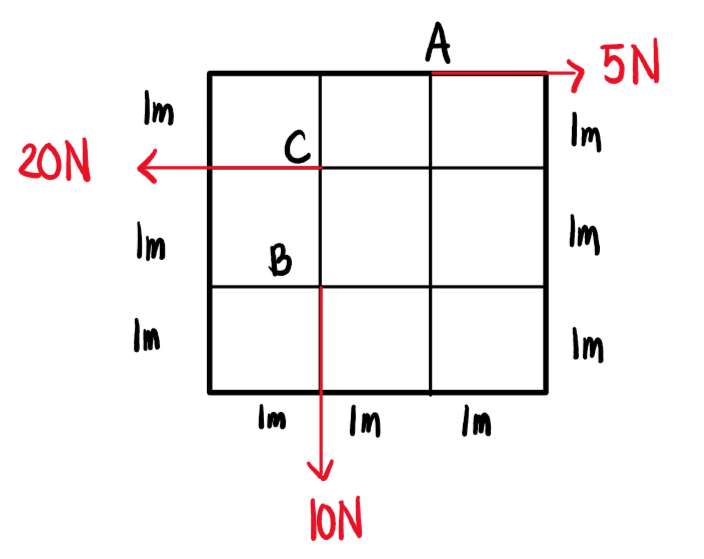
Diagram Diagram Diagram

See images:

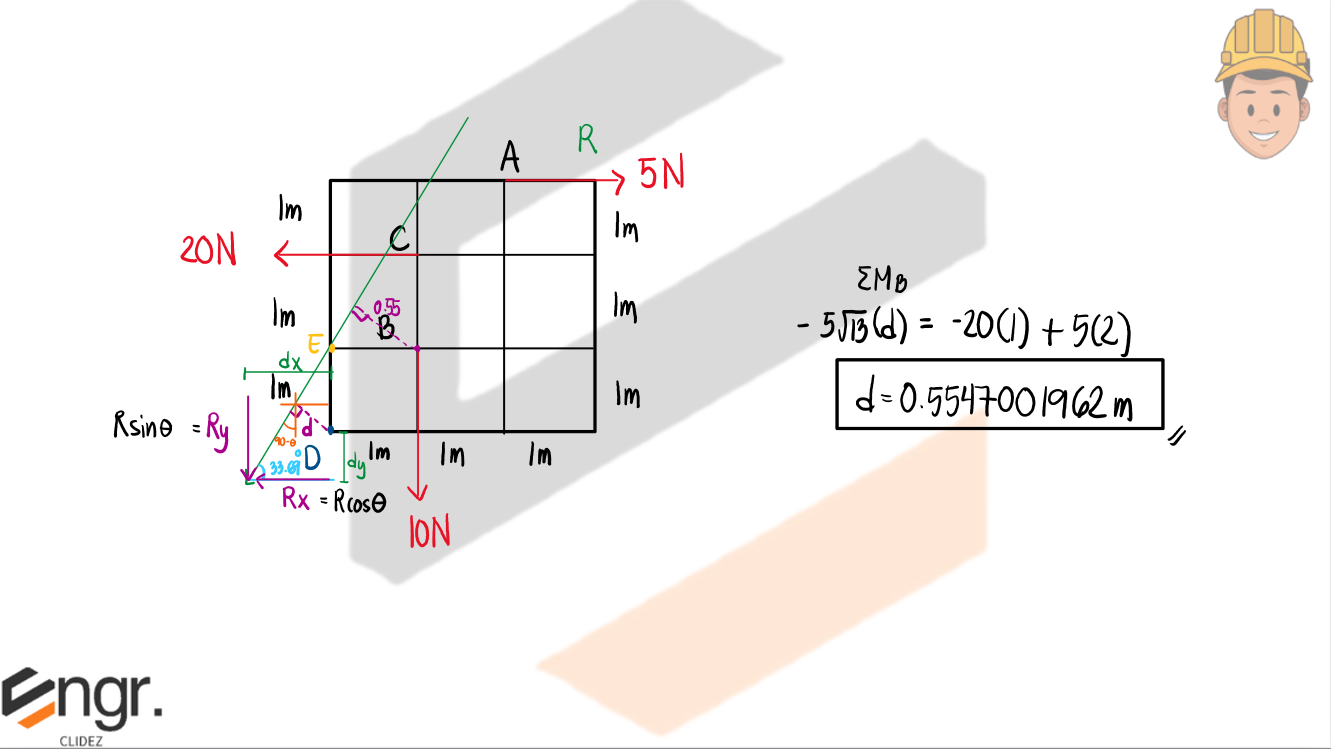
Solution Solution Solution Solution Solution
    Below is a scaled drawing of the figure (modeled using AutoCad).
Solution
    We can obtain the moment caused by the resultant force about point D so that we can transfer the resultant so that it intersects point D. The moment (couple) will be applied at point D for clarity.
Solution
    Finally, we have this resultant-couple system that replaces the system above.
Solution

Problem 2:

For the beam shown, beam ABC is supporting beam CD.
Which of the following most nearly gives the reaction at C in kN.
A. 250
B. 150
C. 100
D. 200

Which of the following most nearly gives the reaction at D in kN.
A. 250
B. 150
C. 100
D. 200

Which of the following most nearly gives the value of "x" if the reaction at B is 380 N.
A. 1
B. 1.5
C. 2
D. 3

Diagram Diagram Diagram

See images:

Solution Solution Solution Solution

Problem 3:

Refer to the image shown:

Diagram Diagram Diagram

See images:

Solution Solution Solution Solution

Problem 4:

Refer to the image shown:

Diagram Diagram Diagram

See images:

Solution Solution Solution Solution

Problem 5:

Refer to the image shown:

Diagram Diagram Diagram

See images:

Solution Solution Solution Solution

Problem 6:

Refer to the image shown:

Diagram Diagram Diagram

See images:

Solution Solution Solution Solution

Problem 7:

Refer to the image shown:

Diagram Diagram Diagram

See images:

Solution Solution Solution Solution

Problem 8:

Refer to the image shown:

Diagram Diagram Diagram

See images:

Solution Solution Solution Solution
-->
Scroll to zoom