Equilibrium of Concurrent Force Systems

Problem 1 (Tension in Cables):

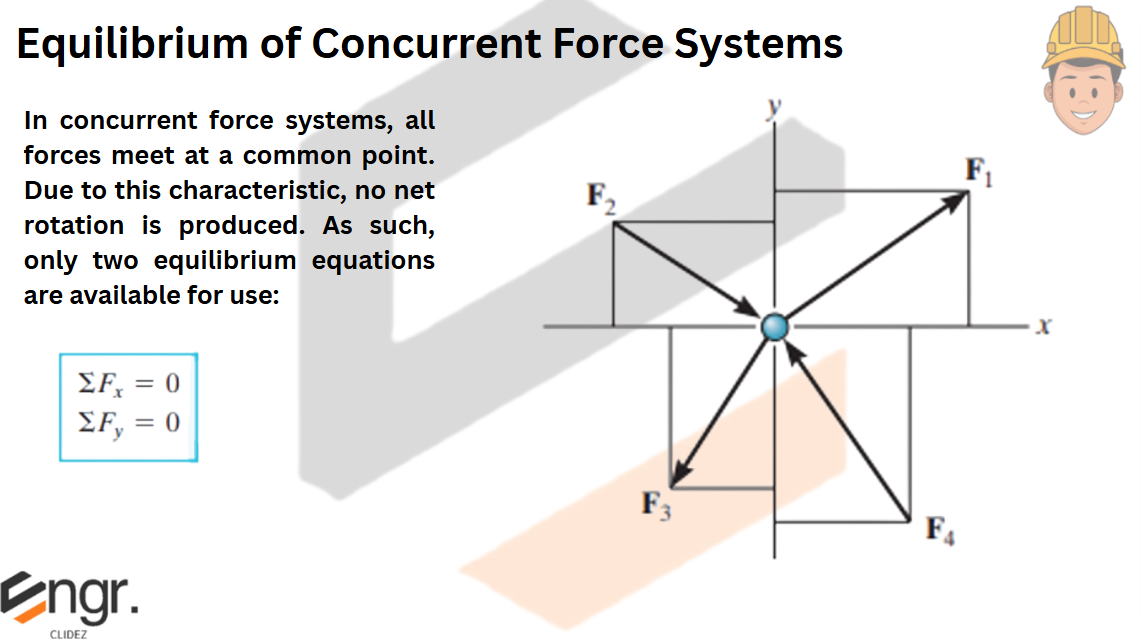
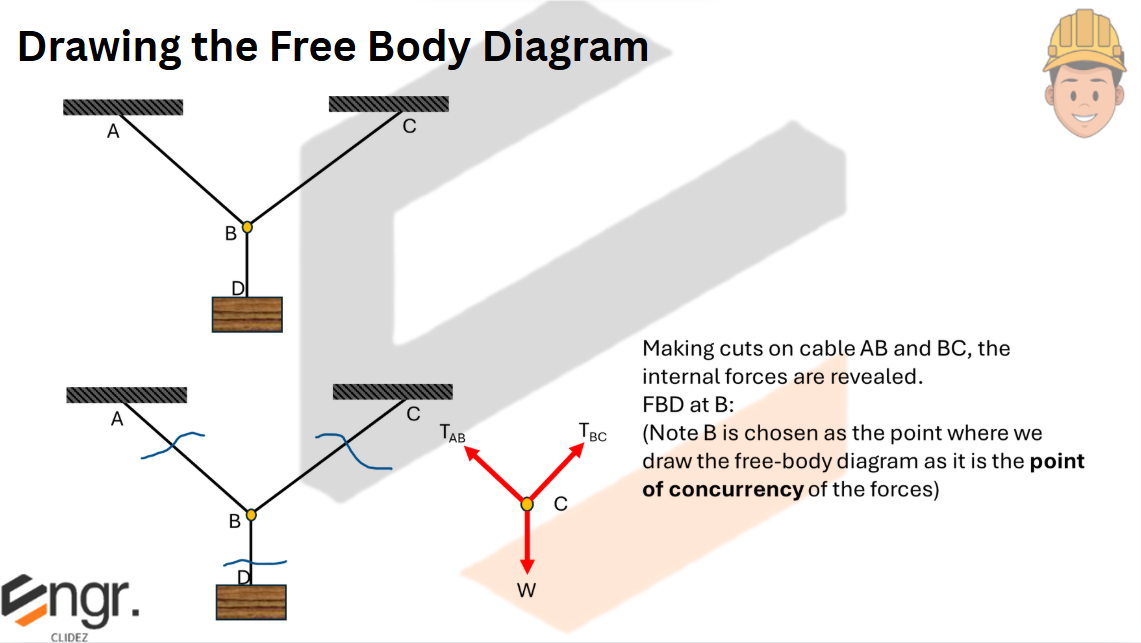
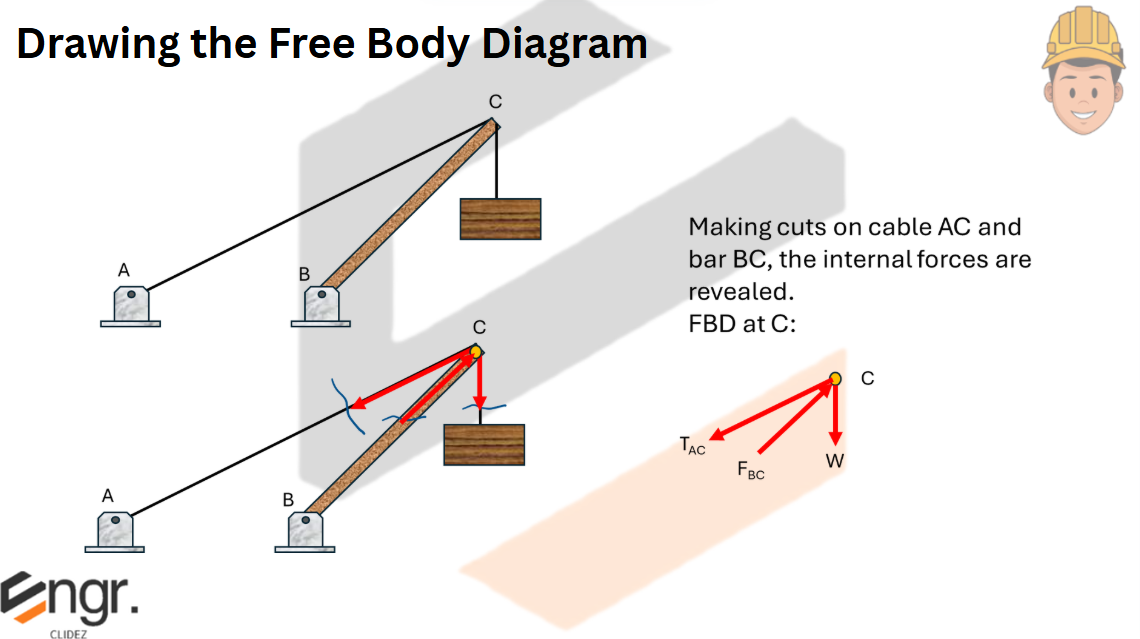
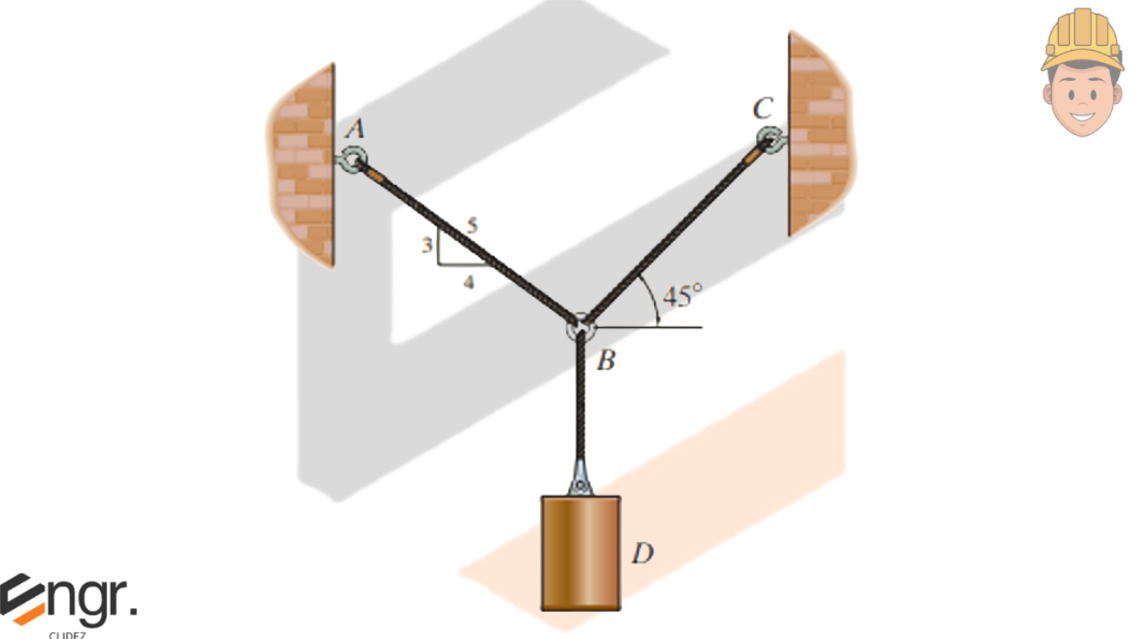
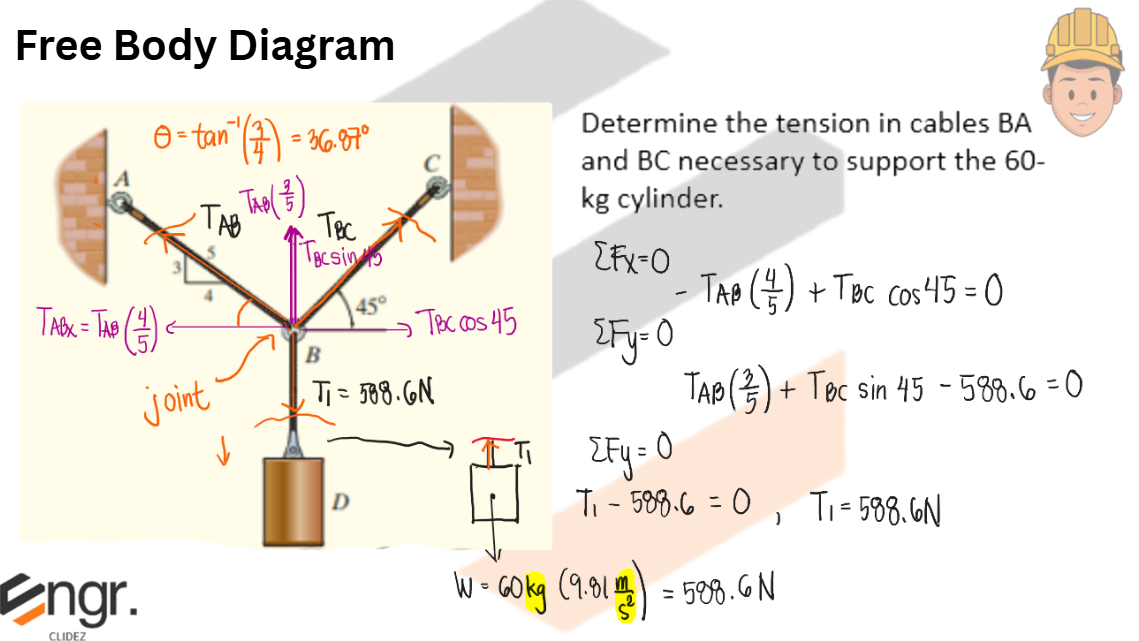
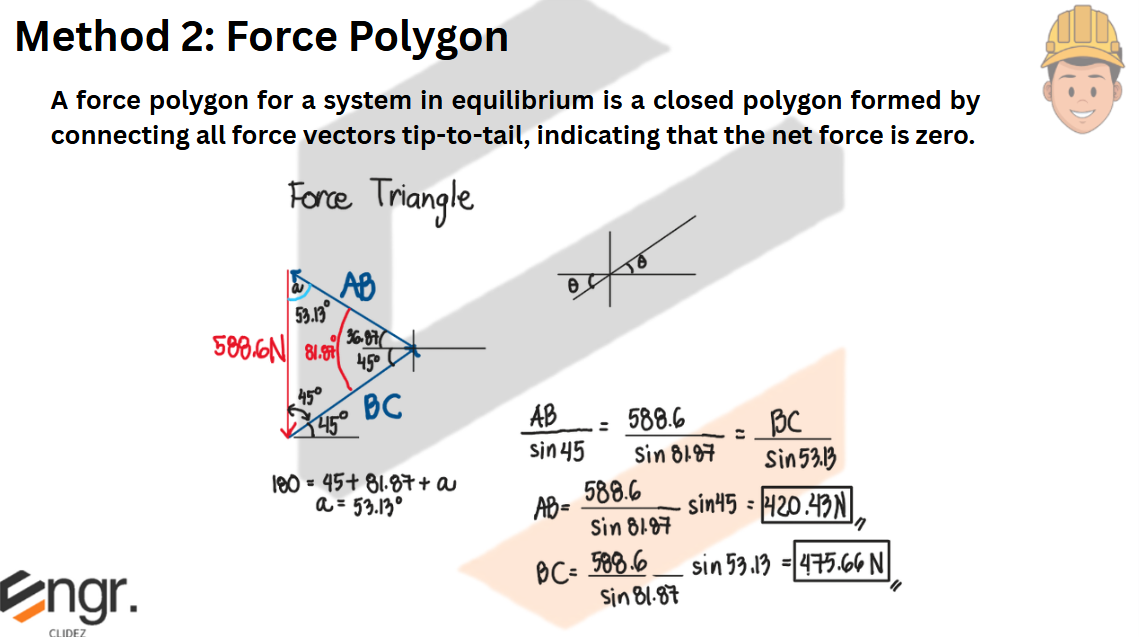
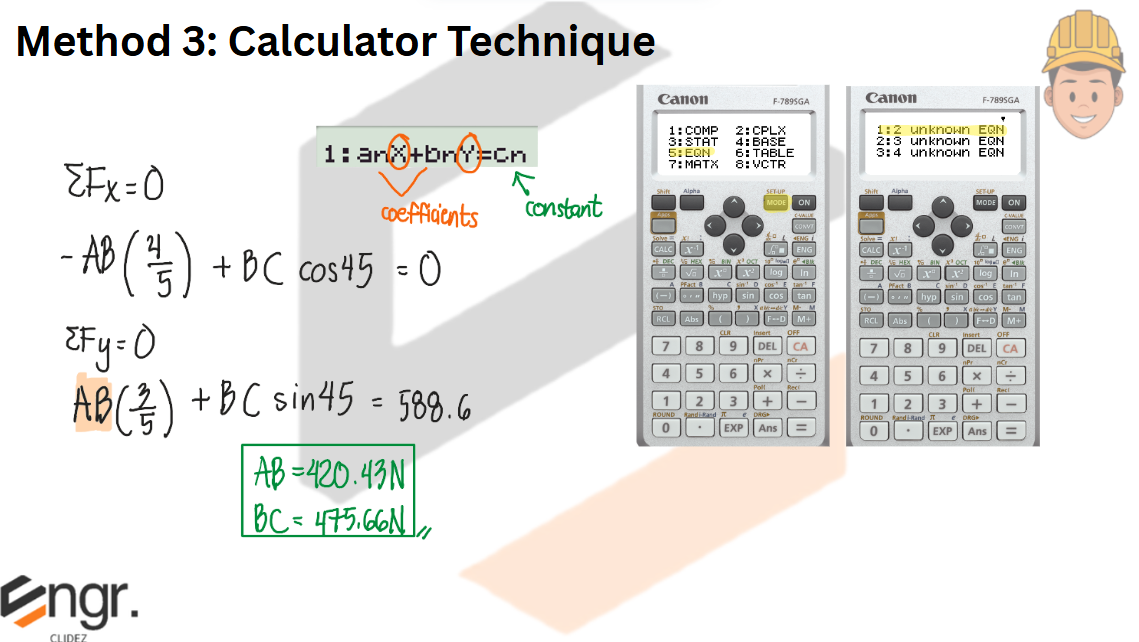
Determine the tension in cables AB and BC necessary to support the 60-kg cylinder.

See images:

Problem 2 (Tension in Cables):

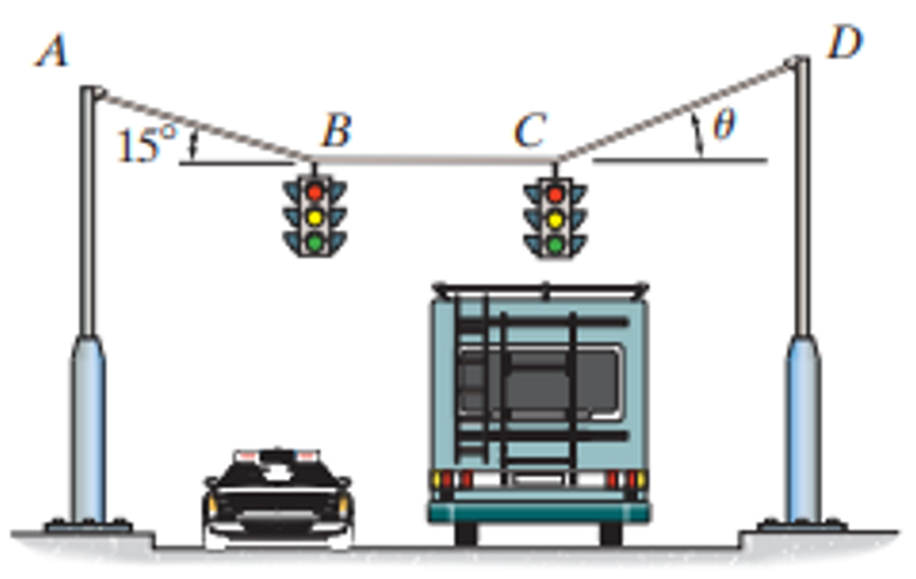
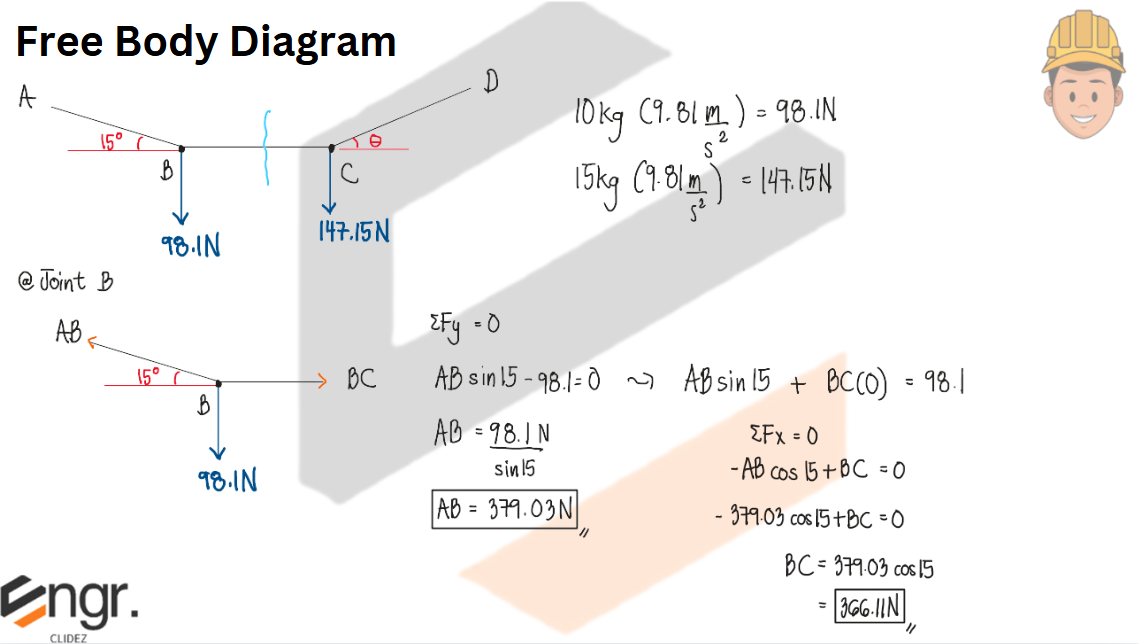
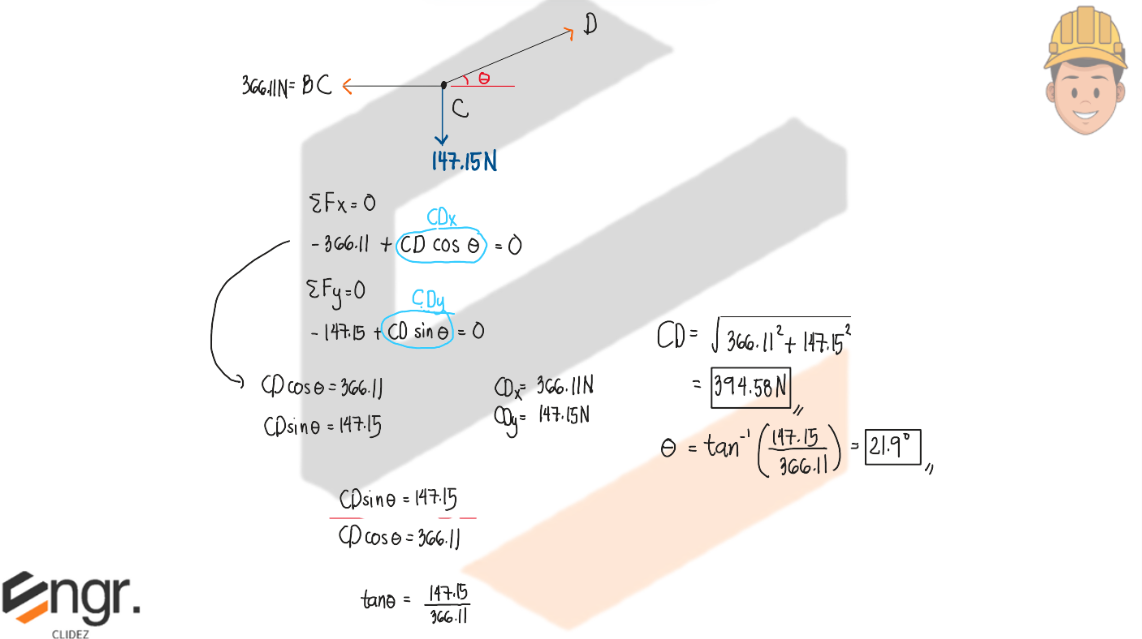
Determine the tension in cables AB, BC, and CD necessary to support the 10-kg and 15-kg traffic lights at B and C, respectively. Also, find the angle ϴ.

See images:

Problem 3 (Tension in Springs):

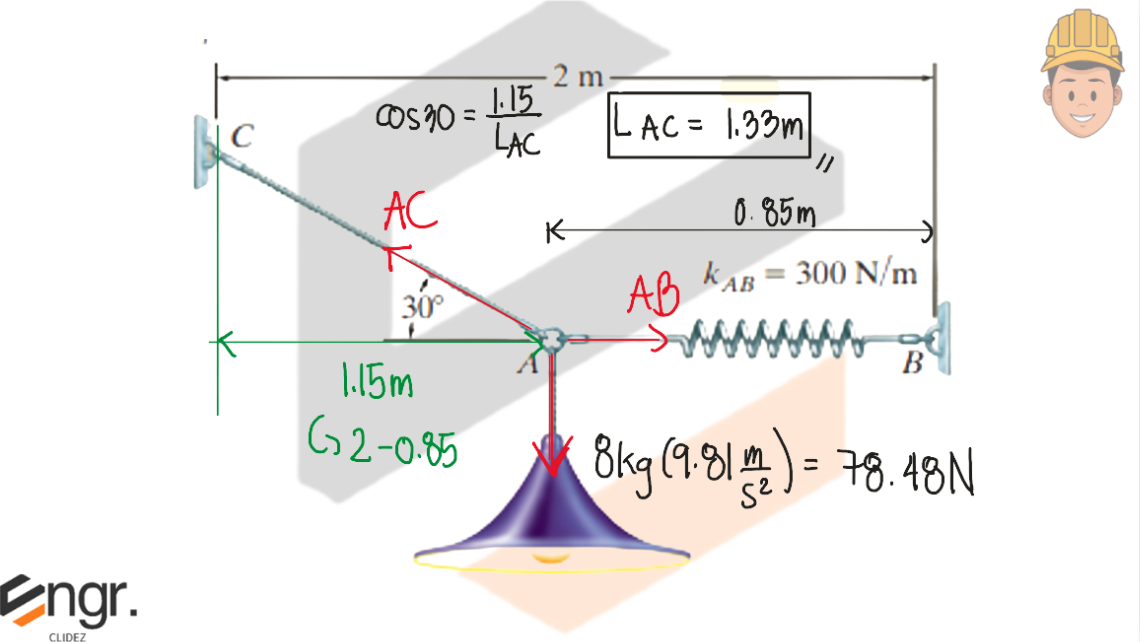
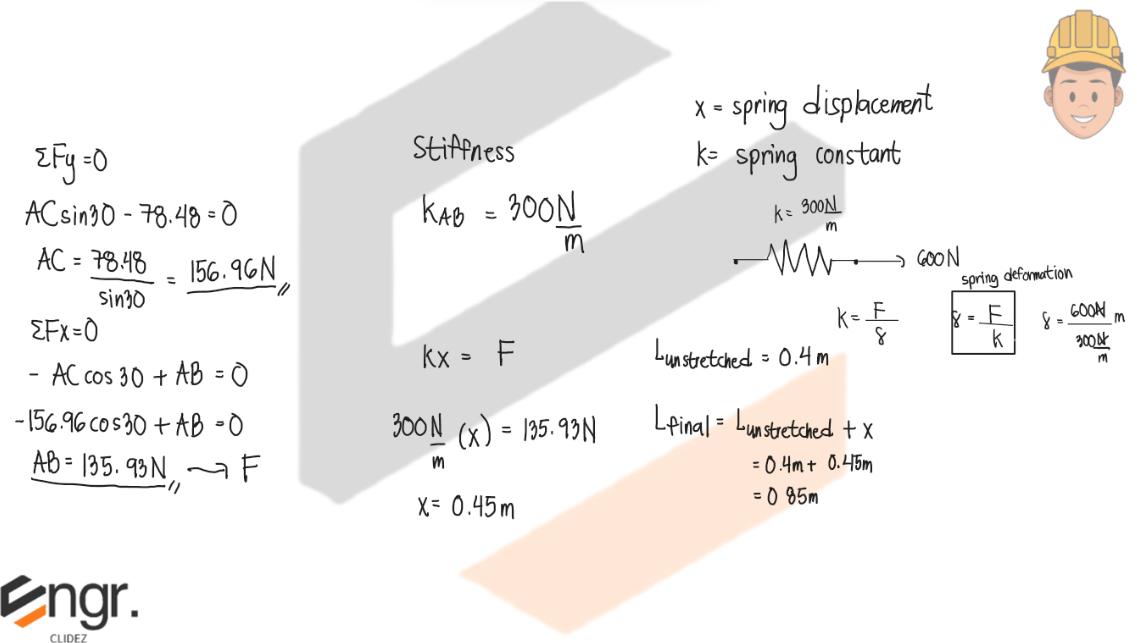
Determine the required length of cord AC so that the 8-kg lamp can be suspended in the position shown. The unstretched length of spring AB is 0.4m, and the spring has a stiffness of k_AB=300N/m

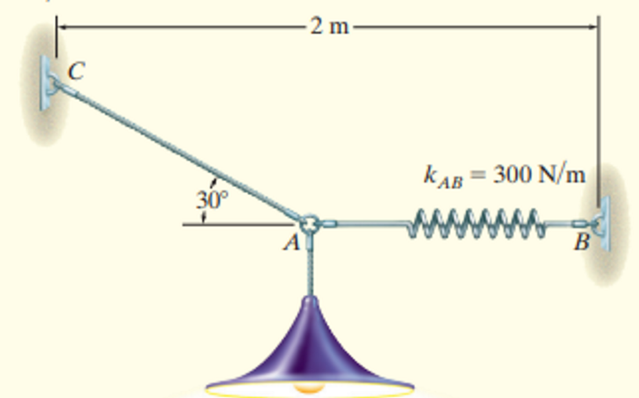
See images:

Problem 4:

A concrete block of weight W holds a ring anchor bolt fastened to two guy wires as shown.
1. Calculate the resultant force acting on the bolt. (10.9kN)
2. Determine the angle which the resultant pull makes with the horizontal. (54.5º)
3. To prevent uplift, what is the minimum weight of the concrete block W if the required factor of safety is 1.3? (11.53kN)

See images:

Problem 5:

A boom supports a 100N load as shown below. If the tension in the cable is 200N,
1. Find the angle α. (21.47º)
2. Find the angle θ. (42.94º)
3. Find the force in the boom. (254.24N)

See images:

Problem 6:

Refer to the image shown. Cylinder 1 weighs 20kN, cylinder 2 weighs 40kN, and cylinder 3 weighs 30kN. The surface along point D is inclined 60º with the horizontal.
1. Determine the reaction at A. (5.78kN)
2. Determine the reaction at D. (6.67kN)
3. Determine the reaction at C. (46.67kN)

See images:

Problem 7:

Force A = 6kN
Force B = 2.4kN
Angle β = 30º
1. The resultant of the three forces, A, B, and C is 3.6kN and it acts along the y-axis. What is the angle θ? (23.6º)
2. If the resultant of the three forces A, B, and C is 5.4kN and it acts along the y-axis, what is the value of C if θ=45º? (2.16kN)
3. If the angle θ=60º and the force C = 3kN, how much is the resultant pulling force on the eyebolt? (6.7kN)

See images:

Problem 8:

A hollow right circular cylinder of radius 0.5m is open at both ends and rests on a smooth horizontal plane. Inside the cylinder are two spheres having weights w₁=10kN and w₂=15kN and radius r₁=0.20m and r₂=0.40m, respectively, as shown. Neglect friction.
a. Determine the horizontal reaction of w₁ on the side of the cylinder. (Ans. 8.95kN)
b. Determine the vertical reaction of w₂ at the horizontal plane. (Ans. 25.30kN)
c. Determine the minimum weight Q of the cylinder in order for it not to tip over. (Ans. 8kN)

See images: