Cables are classified into parabolic, catenary, and segmented cables.
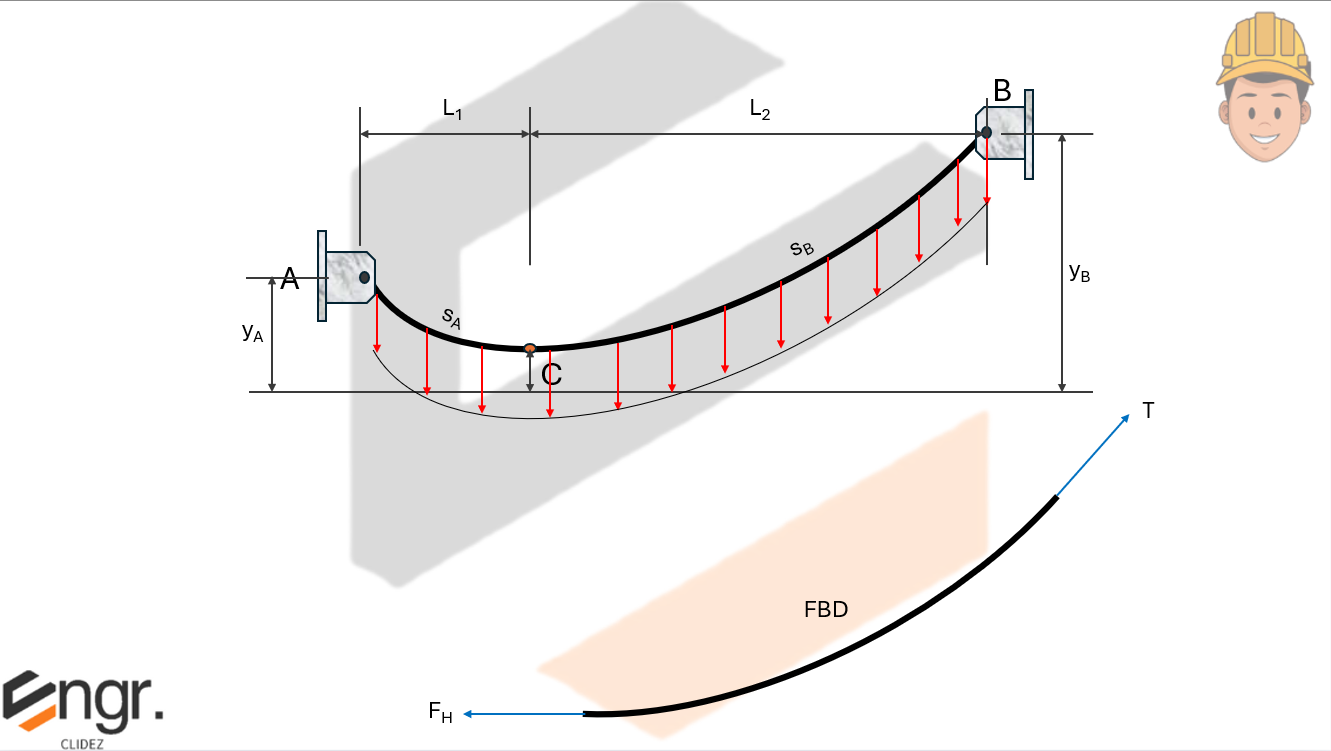
Parabolic Cable - is one in which the load is distributed uniformly in a horizontal length. An example of a parabolic cable is a wire suspended at its end. Consider a wire supported at A and B as shown with its lowest point at C. Note that tensile forces act tangent to any point along the curve.
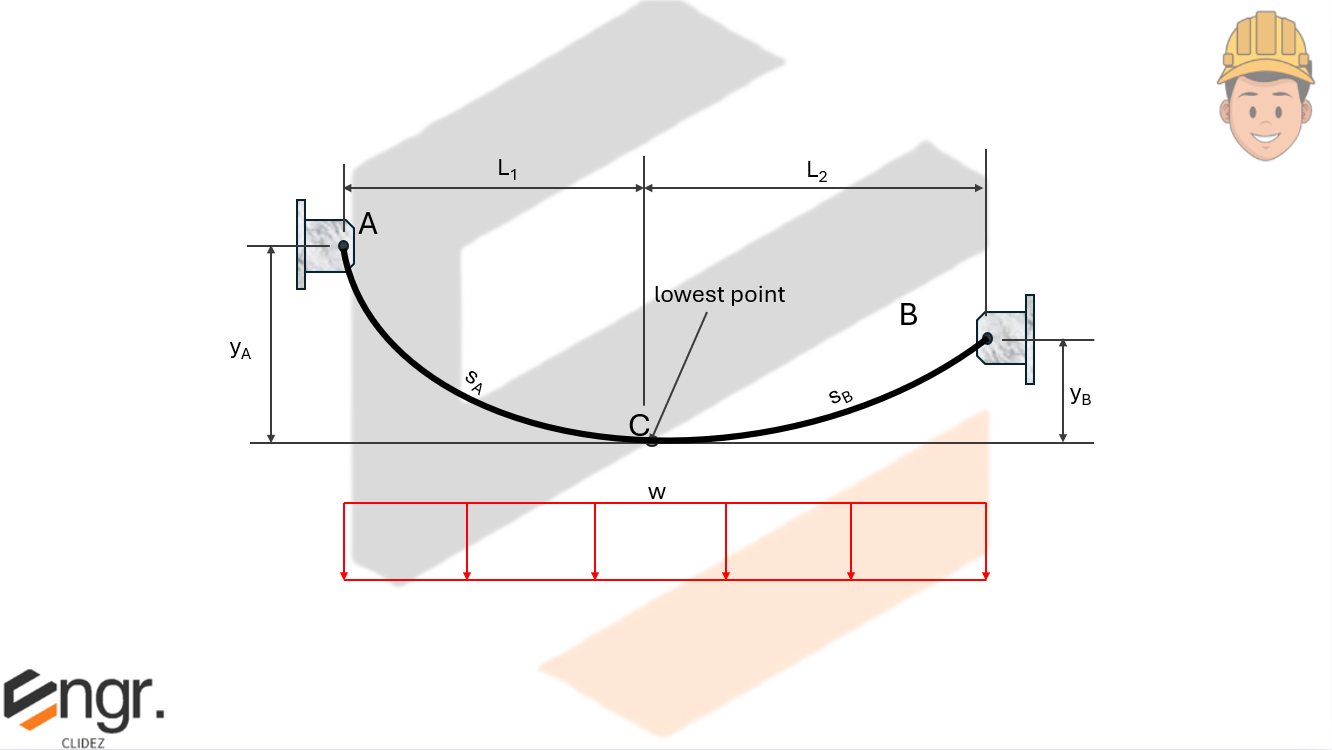
The general equation of a catenary curve (with origin at the lowest point of the cable) is:
Where:
For a non-symmetrical cable where supports A and B are at different elevations:
The vertical difference between supports is then:
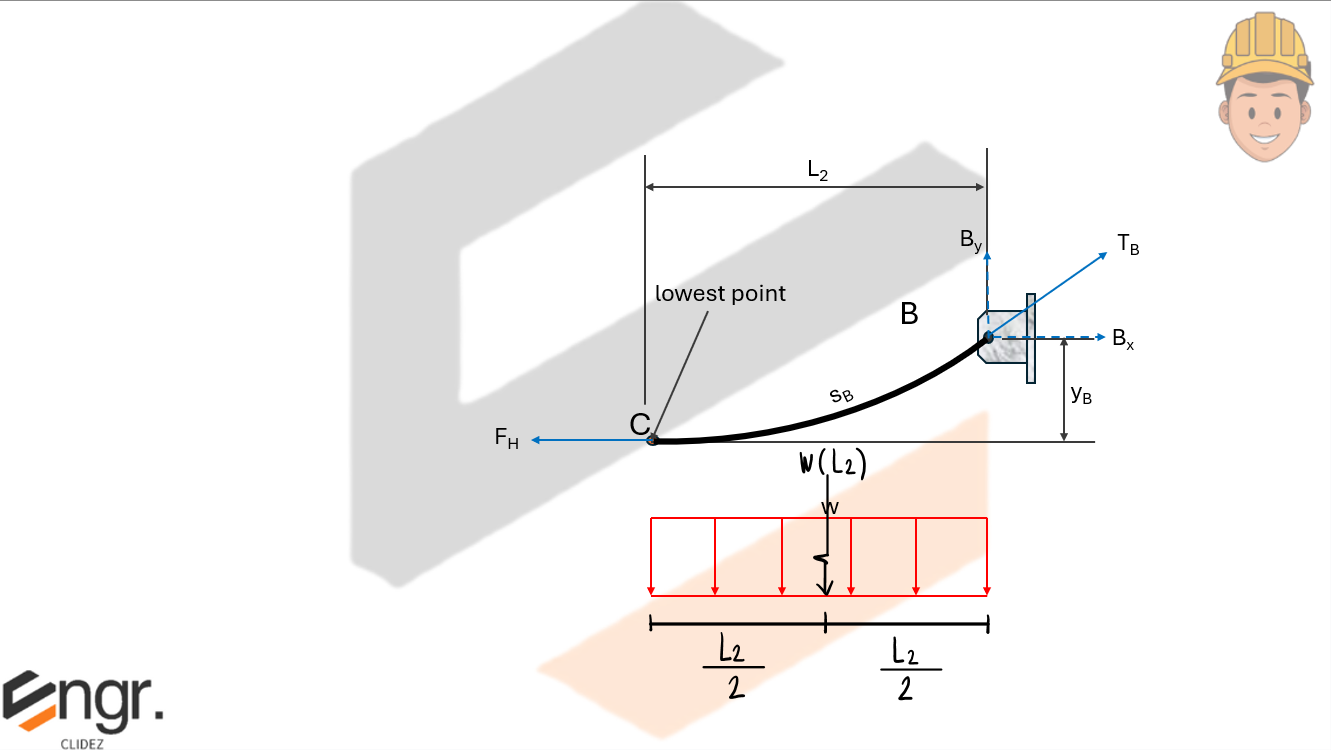
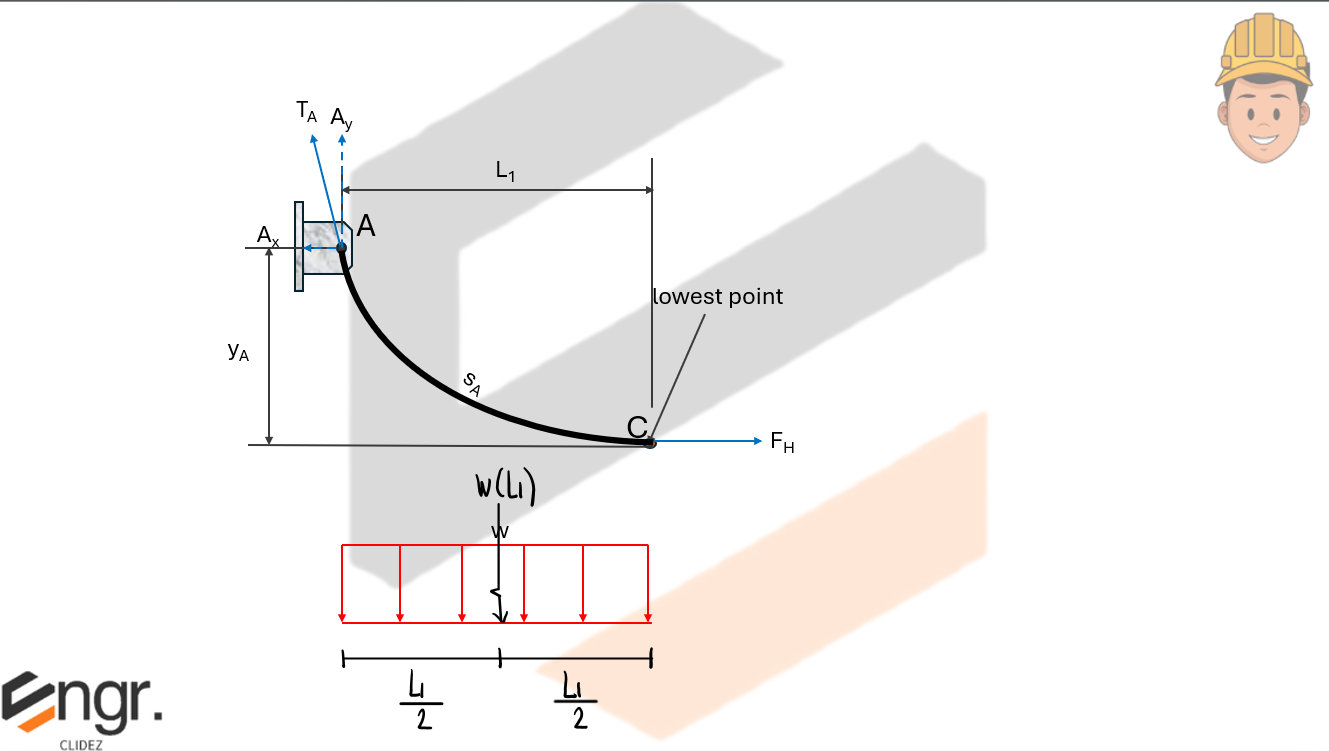
Horizontal tension is given by:
Total tension at a point \( x \) is:
Arc length from the lowest point C to support A is:
Arc length from the lowest point C to support B is:
Total cable length from A to B is:
The integral form of the cable length between two points (e.g. from A to B) is:
For the specific catenary equation \( y(x) = a \cosh\left( \frac{x}{a} \right) - a \), this becomes:
Segmented Cables
A cable of negligible self-weight that supports multiple concentrated loads forms a series of straight-line segments. Each segment experiences a constant tensile force, and the shape of the cable adjusts to satisfy the equilibrium conditions at each point of loading. Analyzing such systems involves applying the principles of equilibrium to both concurrent and non-concurrent force systems at the joints and supports.




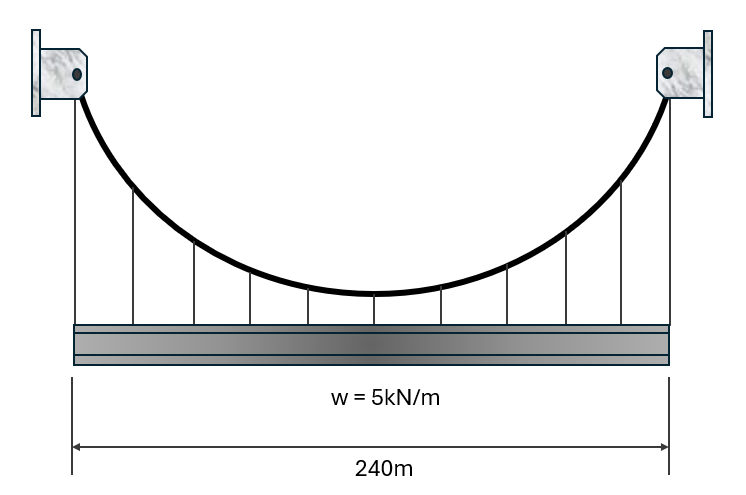
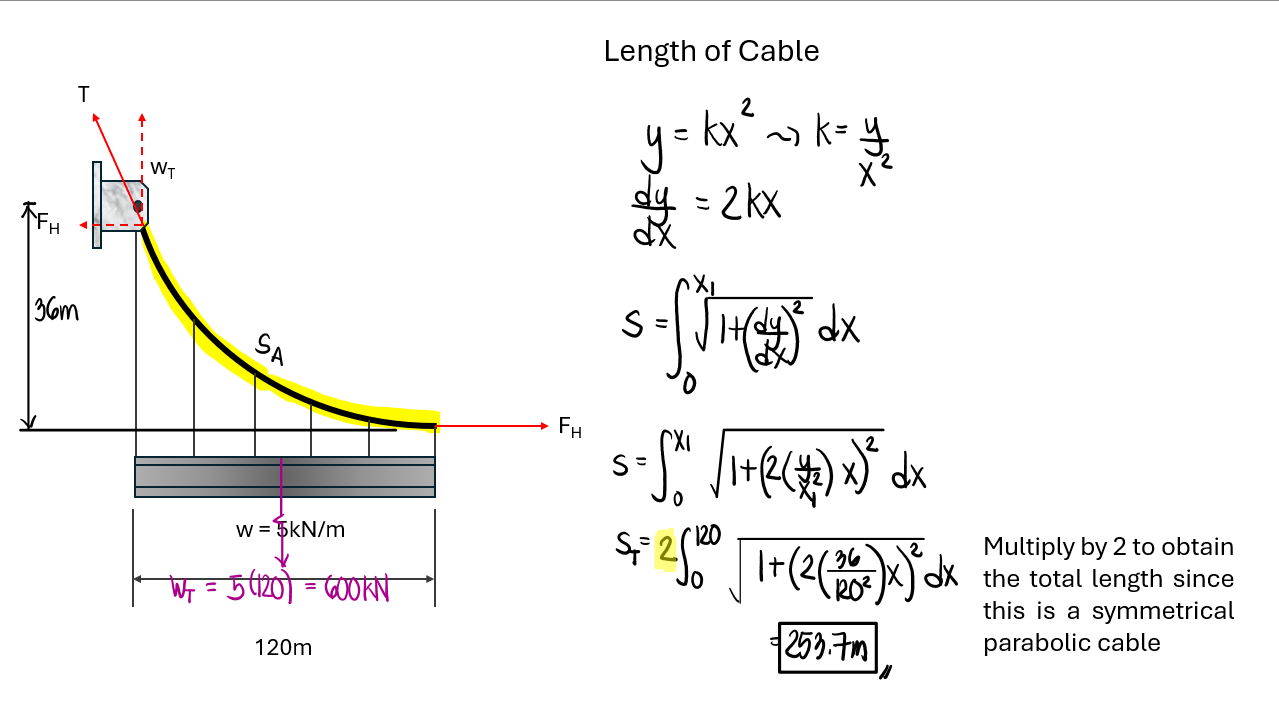
The cable shown carries a uniform load of 5kN/m. The lowest point of the cable is 36m below the supports.
Determine the minimum tension in the cable
A. 600kN
B. 1000kN
C. 1166kN
D. 1616kN
Determine the maximum tension in the cable
A.600kN
B. 1000kN
C. 1166kN
D. 1616kN
Determine the angle that the maximum tension makes with the horizontal
A. 59°
B. 31°
C. 42°
D. 48°
Determine the length of the cable
A. 240m
B. 245m
C. 254m
D. 258m


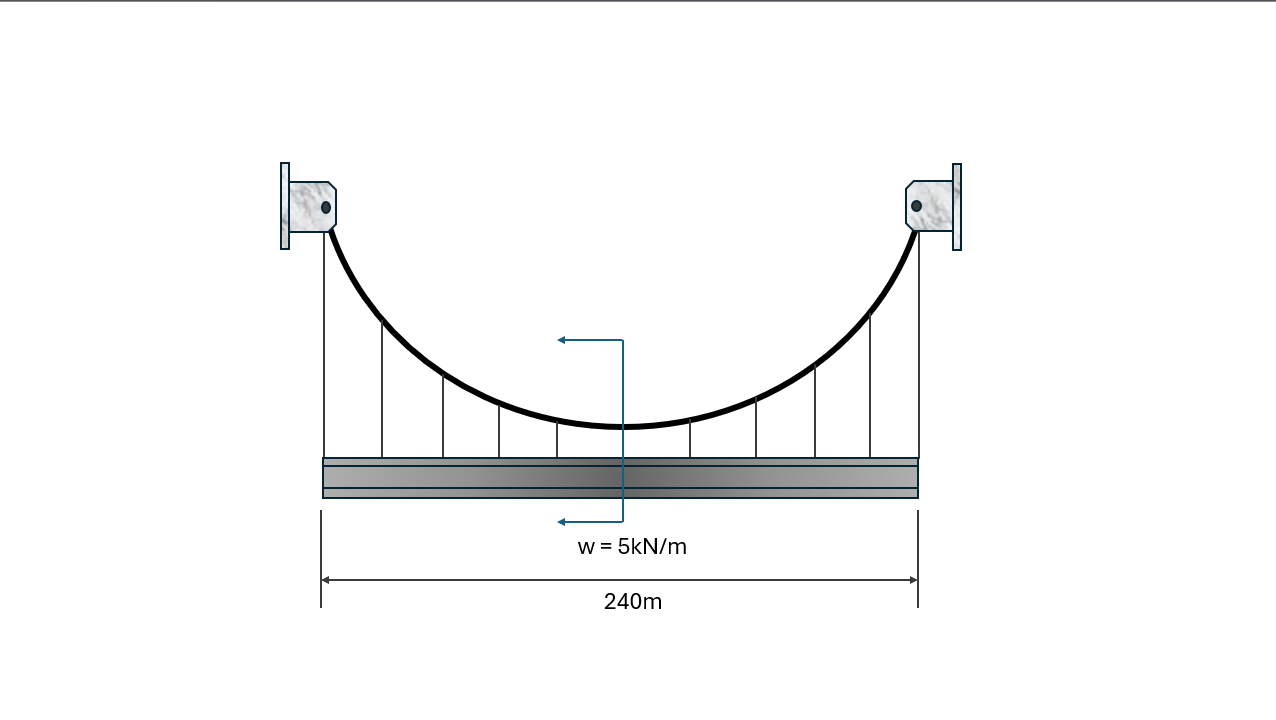
Cut the cable at the lowest point and let us consider the left side of the cut.
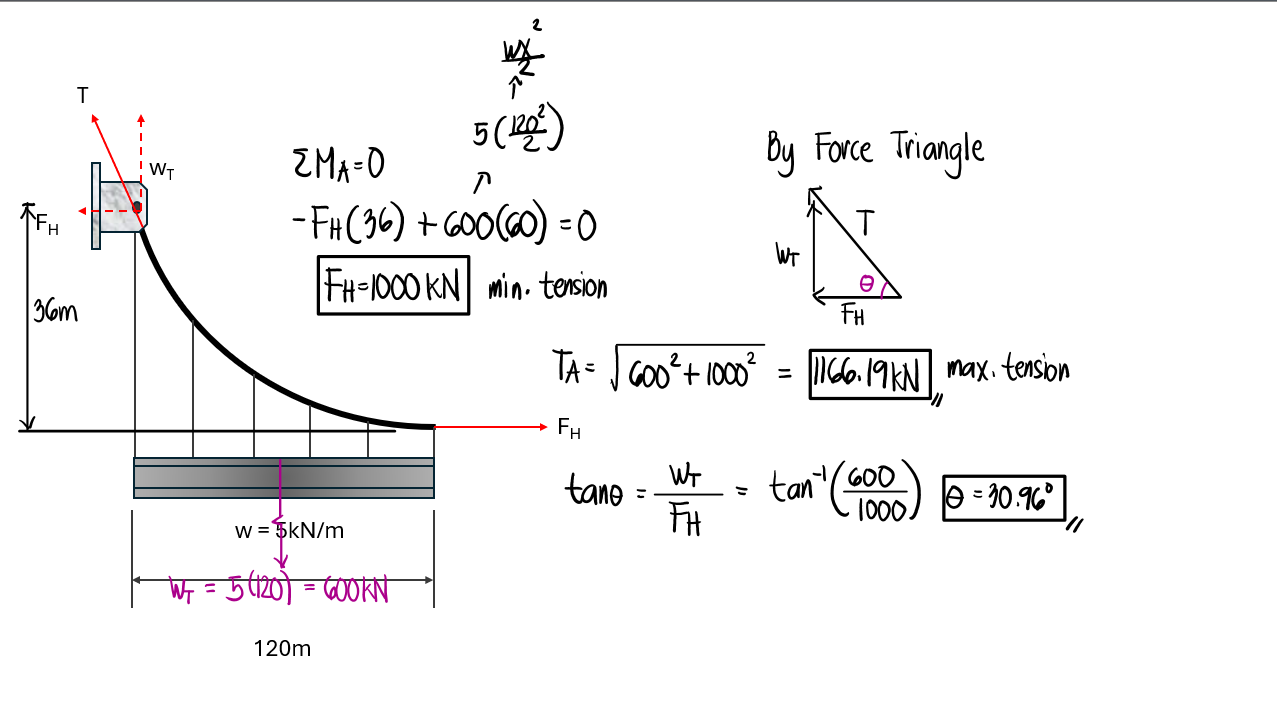
The system consists of a force triangle. The minimum tension occurs at the lowest point, while the maximum tension occurs at the point where the slope is the largest (at the support). The lowest point of the cable is 36m below the support, as stated in the problem.
The integral expression below only solve the arc length up to the vertex, considering the left side. Just multiply the result by 2 for symmetrical parabolic cables to obtain the total length.

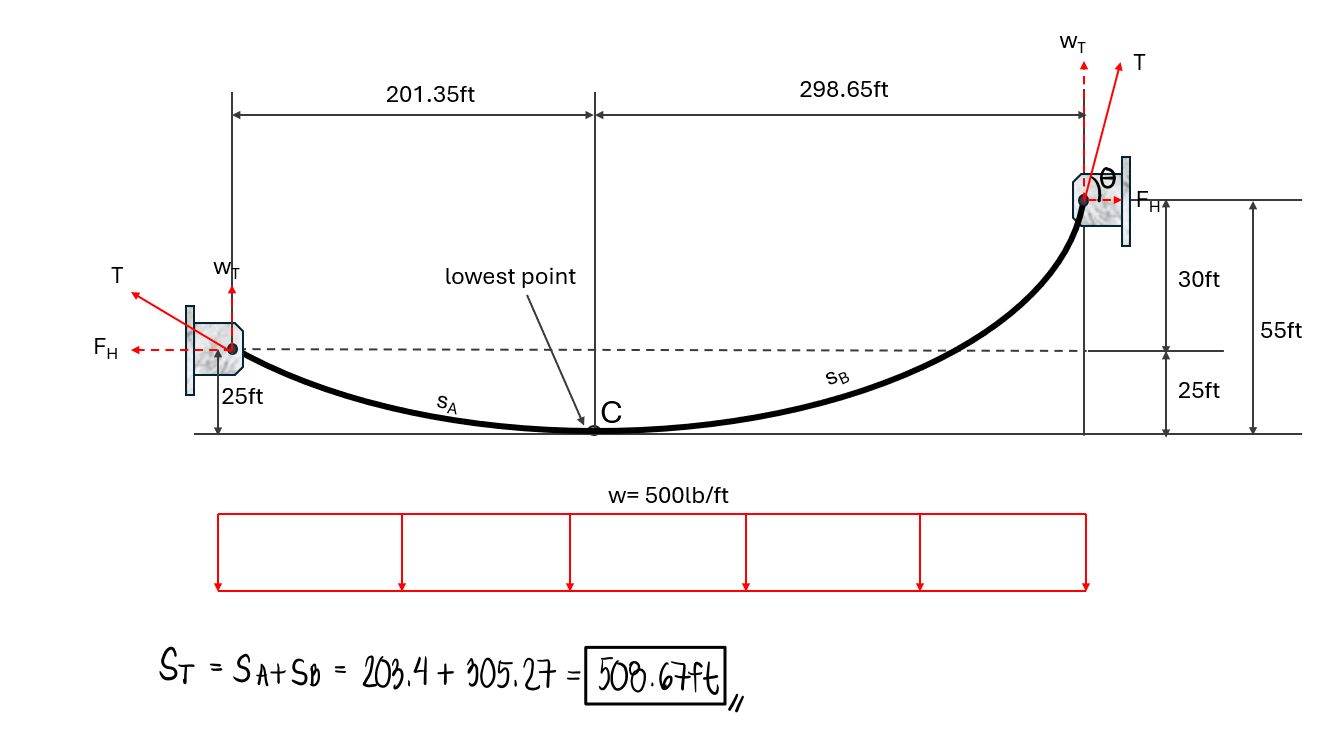
A cable carries a uniformly distributed load of 500lb per foot of horizontal length. The supports are 500ft apart and the left support is 30ft lower than the right support. The lowest point on the cable is 25ft below the left support. Determine:
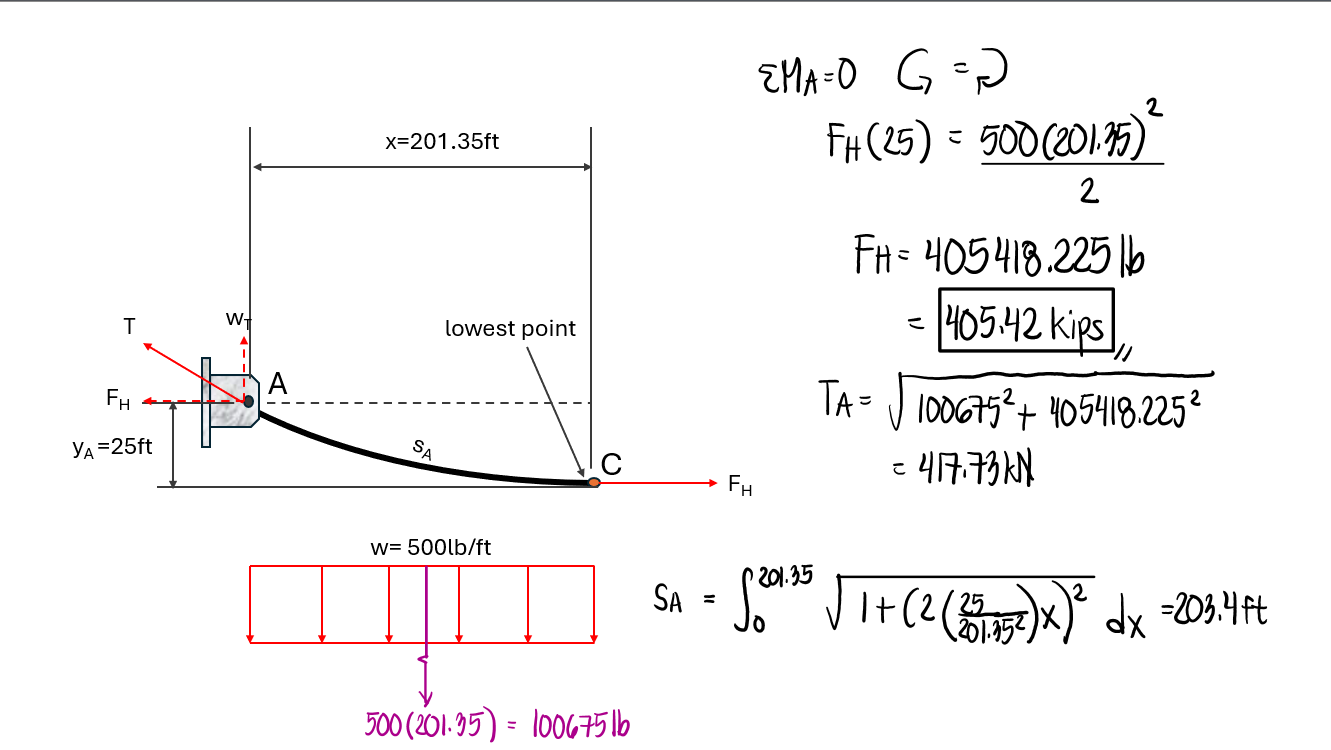
The minimum tension in the cable.
A. 405k
B. 432k
C. 443k
D. 418k
The maximum tension in the cable.
A. 405k
B. 432k
C. 443k
D. 418k
The angle between the cable and the horizontal at the right support.
A. 20.2°
B. 22.2°
C. 21.2°
D. 23.2°
The length of the cable
A. 500ft
B. 523ft
C. 509ft
D. 515ft



To obtain the value of x, we use the squared property of a parabola (SPP):
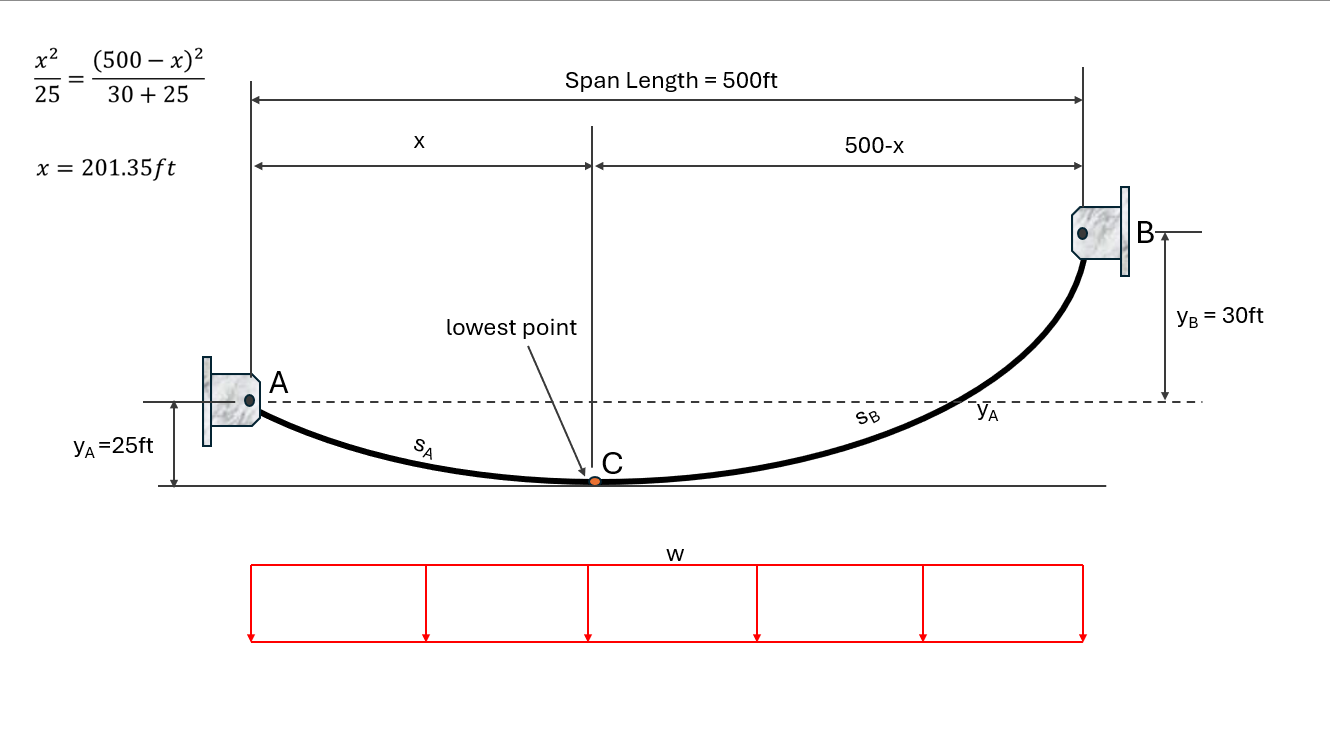
Since this is an unsymmetrical parabolic cable, we will analyze the left side and the right side separately after cutting the cable at the lowest point.
Generally, because the maximum tension occurs at the point wherein the slope is the largest, it naturally means that the maximum tension occurs at the side where the horizontal distance is also the largest. In this case, the right side has a horizontal span of 298.65ft, so the maximum tension will occur at the support at B.
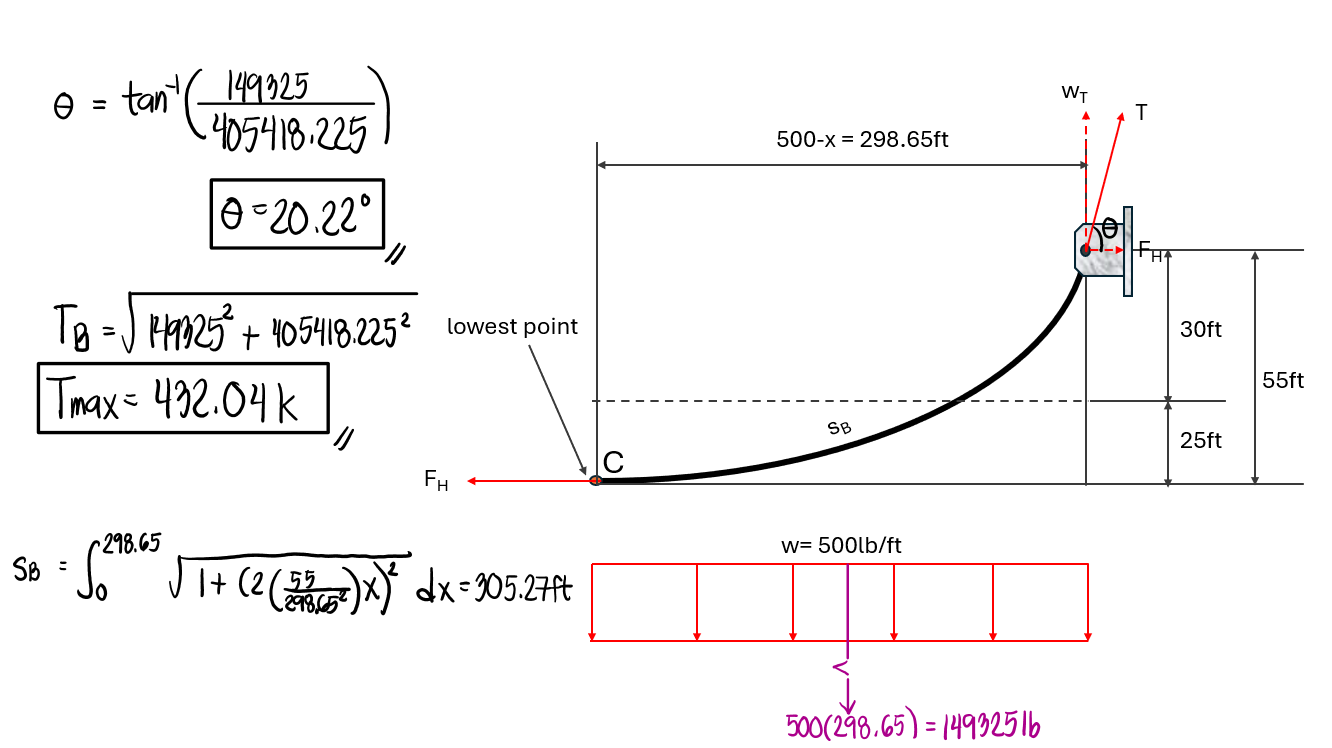
To obtain the total cable length, we need to add sA and sB.
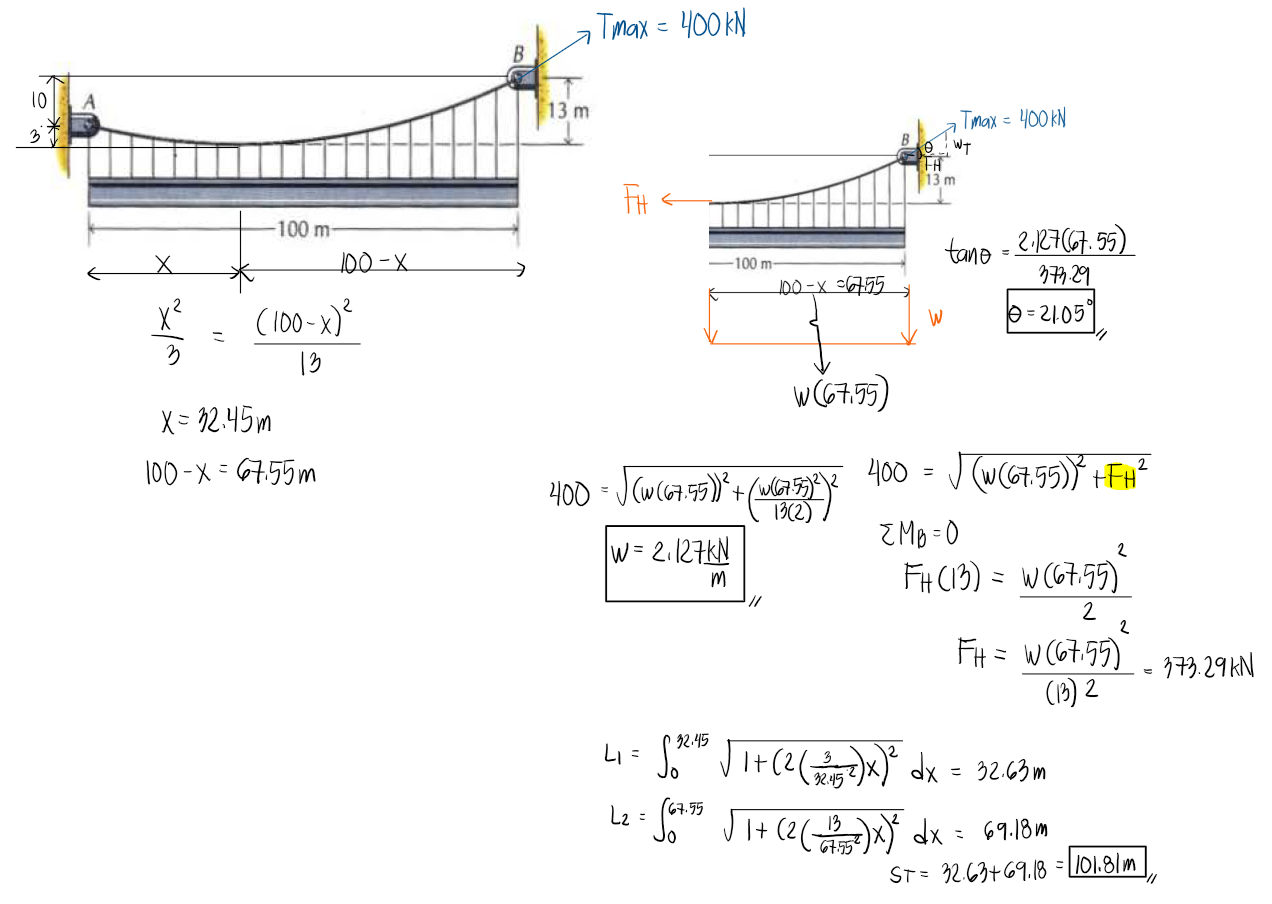
The maximum tension of the cable shown is 400kN and it has a span of 100m. It carries a uniform load, w, in kN/m. The distance between A and B is 10m and B is above point A. The distance from point B to the lowest point of the cable is 13m, determine:
Determine the angle between the cable and the horizontal at the right support.
A. 21.1°
B. 68.9°
C. 30.4°
D. 59.6°
Determine the uniform load, w
A. 2.127kN/m
B. 3.127kN/m
C. 4.127kN/m
D. 1.127kN/m
Determine the length of the cable
A. 50.91m
B. 101.82m
C. 69.2m
D. 138.4m



See images:



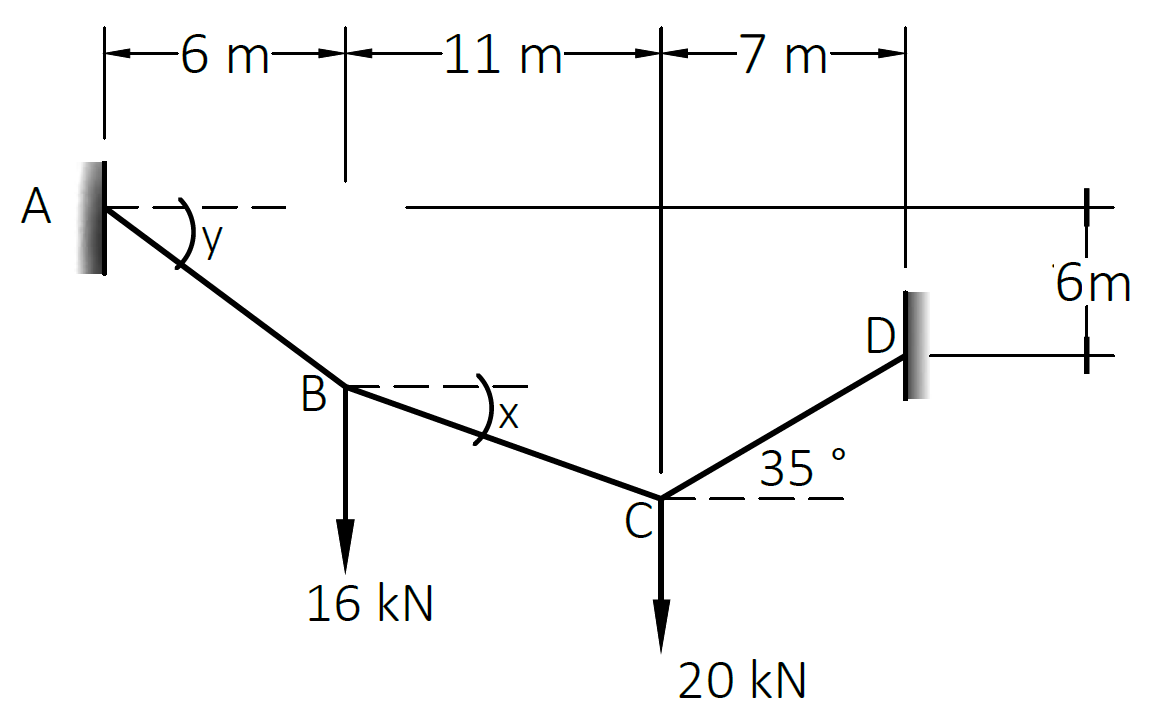
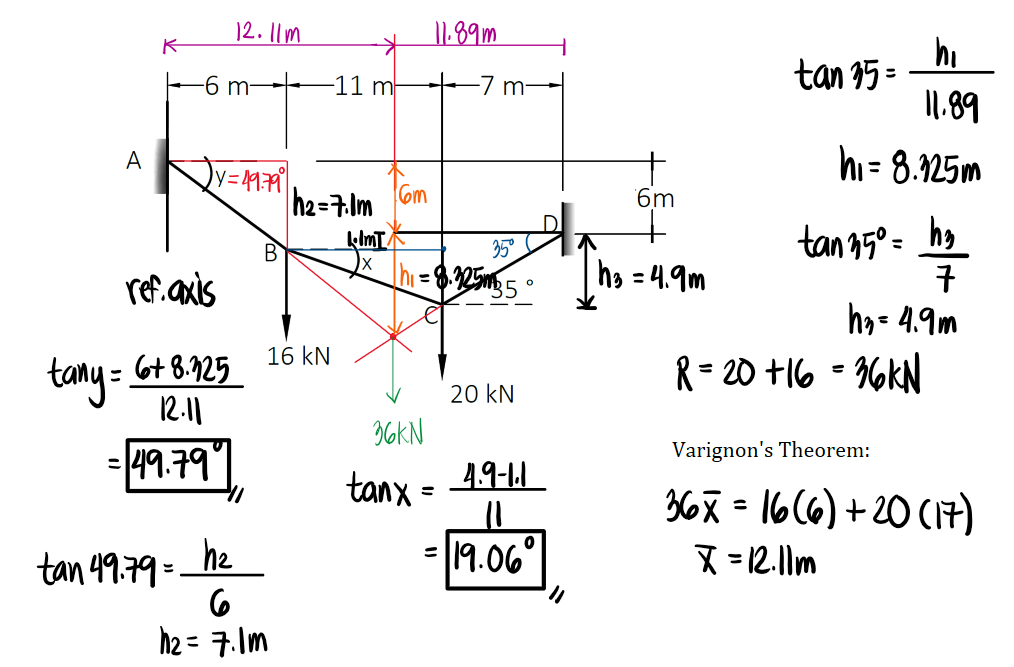
For the cable shown below, determine the values of angle x and y, as well as the total length of the cable. Ans. (x=19.079°, y=49.78°, L=29.48m)


Free Body Diagram:
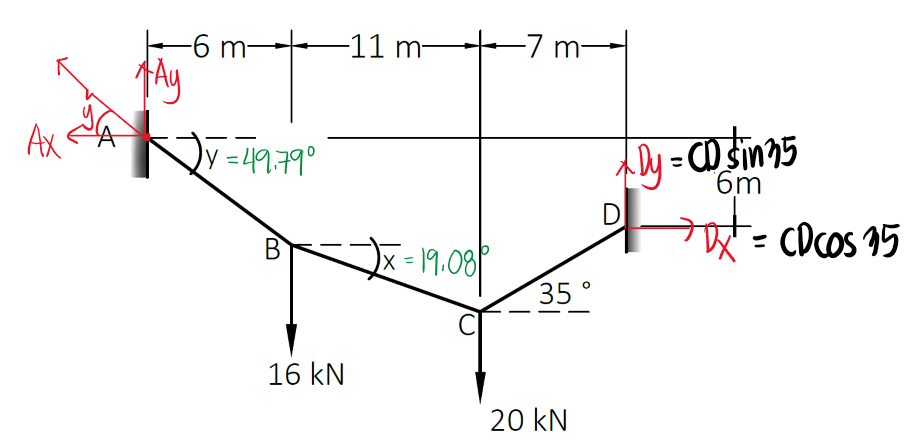
We determine the value of the tension in cable CD by summing up moments about point A. Note the the resultant reactions and components of the reactions at A and D (supports) are the same as the cables attached to them.

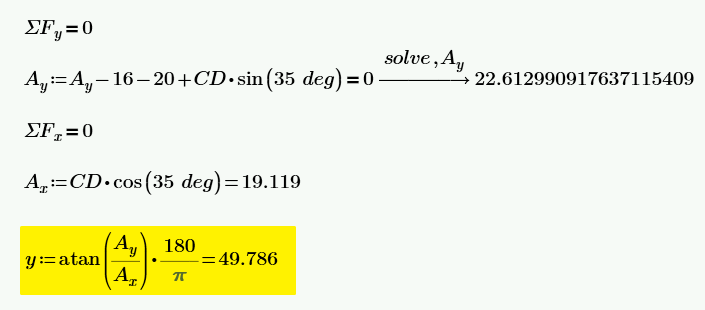
By applying Varignon's theorem, we can locate the resultant of the parallel force system and extend lines AB and CD. Extending the two lines, we observe that they have a point of intersection. The distance from this point of intersection to the left end is equivalent to the location of the resultant force measured from the left end. By applying plane trigonometry, we can obtain the angles x and y.
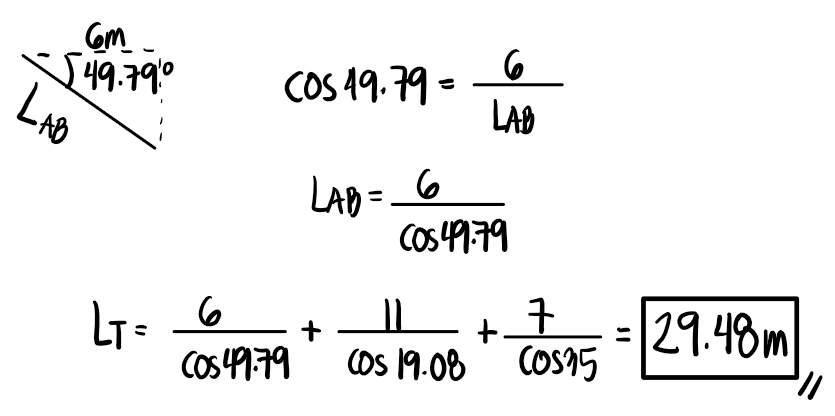
To determine the total length of the cable, we add the lengths of AB, BC, and CD. The relationship of the reference angle and the hypotenuse is shown for AB, and it will also apply for BC and CD.
Refer to the image shown:



See images:




Refer to the image shown:



See images:




Refer to the image shown:



See images:




Refer to the image shown:



See images:



