CE Board Exam Randomizer

Belt Friction

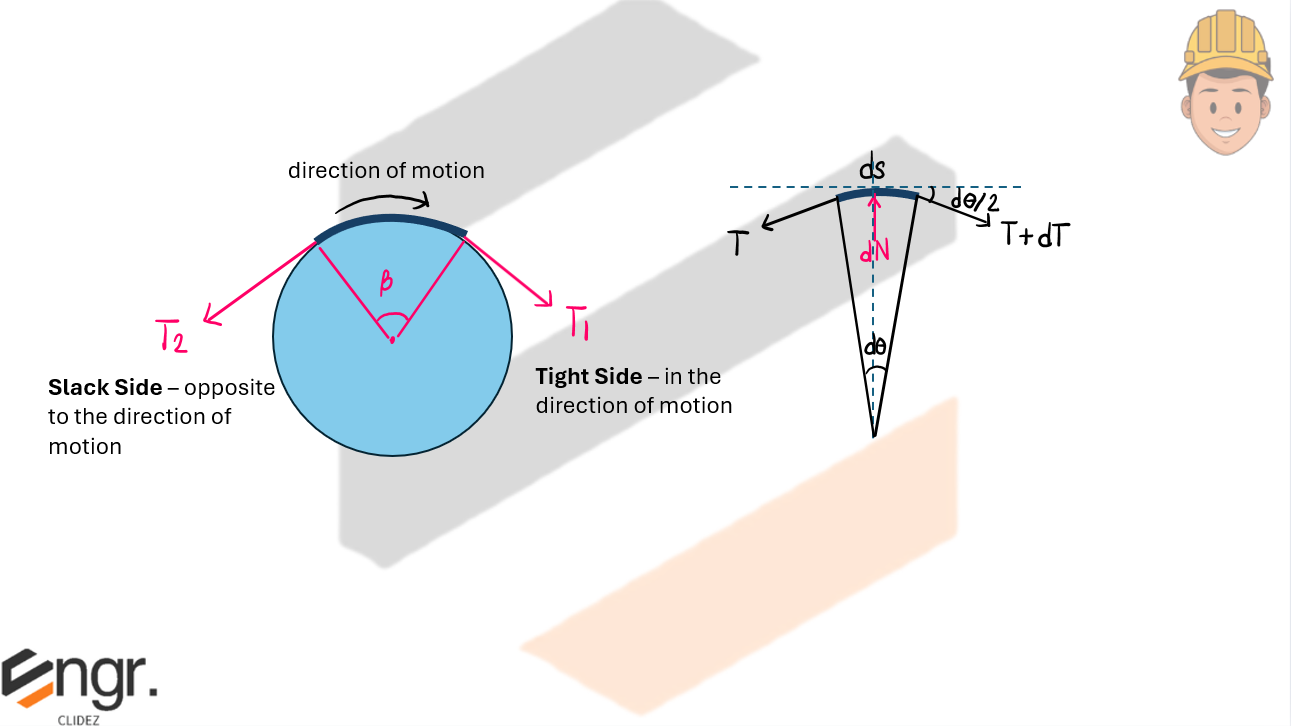
To derive the belt friction equation, consider an infinitesimal element of the belt that subtends a small angle $ d\theta $ on the surface of a pulley. Tension forces on either side of this segment are:

$ T $ — acting tangentially at one edge
$ T + dT $ — acting tangentially at the other edge

These forces are separated by an angle $ d\theta $, so they each deviate from the central direction by $ \frac{d\theta}{2} $. A normal force $ dN $ acts radially inward, and the frictional force $ dF $ opposes the relative slipping motion.

In equilibrium (neglecting second-order small terms), summing forces in the tangential direction yields:

$$ dT = \mu \, dN $$

In the normal direction:

$$ dN = T \, d\theta $$

Substituting into the tangential equation:

$$ dT = \mu T \, d\theta $$

Separating variables:

$$ \frac{dT}{T} = \mu \, d\theta $$

Integrating from $ T_2 $ to $ T_1 $, and from $ 0 $ to $ \beta $:

$$ \int_{T_2}^{T_1} \frac{dT}{T} = \mu \int_0^\beta d\theta $$

$$ \ln\left( \frac{T_1}{T_2} \right) = \mu \beta $$

$${T_1 = T_2 e^{\mu \beta}} $$

This final equation relates the tensions on the tight and slack sides of a belt in contact with a surface over an angle $ \beta $ (in radians), where $ \mu $ is the coefficient of static friction.