Tension Members

Load Combinations for Load and Resistance Factor Design (LRFD)

Combination 1: $1.4D$
Combination 2: $1.2D + 1.6L + 0.5(L_r \text{ or } S \text{ or } R)$
Combination 3: $1.2D + 1.6(L_r \text{ or } S \text{ or } R) + (L \text{ or } 0.5W)$
Combination 4: $1.2D + 1.0W + L + 0.5(L_r \text{ or } S \text{ or } R)$
Combination 5: $1.2D + 1.0E + L + 0.2S$
Combination 6: $0.9D + 1.0W$
Combination 7: $0.9D + 1.0E$

Where:
$D$ = dead load
$L$ = live load due to occupancy
$L_r$ = roof live load
$S$ = snow load
$R$ = rain or ice load
$W$ = wind load
$E$ = earthquake (seismic load)

Load Combinations for Allowable Strength Design (ASD)

Combination 1: $D$
Combination 2: $D + L$
Combination 3: $D + (L_r \text{ or } S \text{ or } R)$
Combination 4: $D + 0.75L + 0.75(L_r \text{ or } S \text{ or } R)$
Combination 5: $D \pm (0.6W \text{ or } 0.7E)$
Combination 6a: $D + 0.75L + 0.75(0.6W) + 0.75(L_r \text{ or } S \text{ or } R)$
Combination 6b: $D + 0.75L \pm 0.75(0.7E) + 0.75S$
Combinations 7 & 8: $0.6D \pm (0.6W \text{ or } 0.7E)$

Where:
$D$ = dead load
$L$ = live load due to occupancy
$L_r$ = roof live load
$S$ = snow load
$R$ = rain or ice load
$W$ = wind load
$E$ = earthquake (seismic load)

NSCP 2010/2015 — Tensile Strength

A tension member is a structural element that carries load primarily through pulling forces along its length. Unlike compression members that resist crushing, tension members resist stretching and are designed to handle axial tensile stresses. Common examples include the diagonal and vertical ties in trusses, bracing in towers, and cables in suspension bridges. Typically made of steel rods, plates, or cables, these members are essential in ensuring stability and strength by effectively transferring loads without buckling.

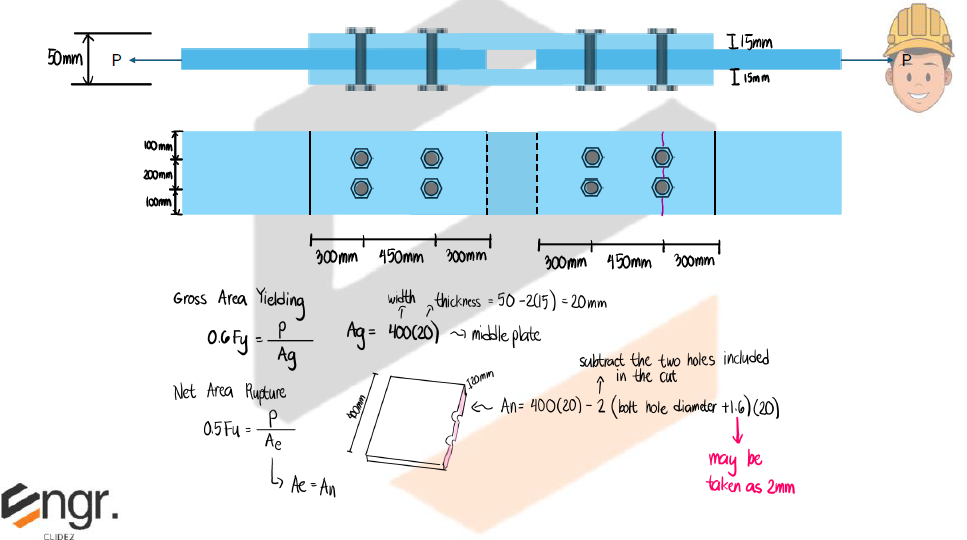
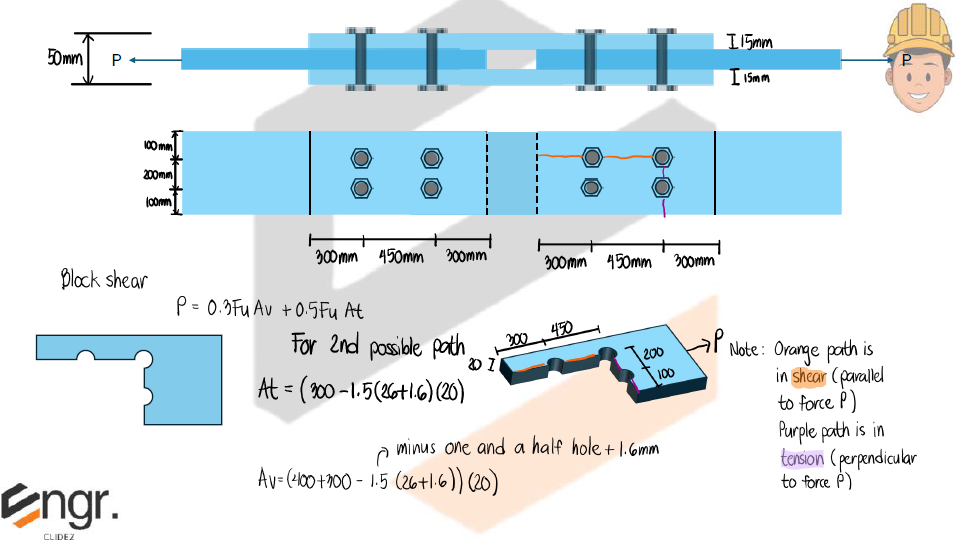
1) Tensile yielding in the gross section

$$P_n = F_y A_g$$ $$\phi = 0.90 \;(\text{LRFD}), \quad \Omega = 1.67 \;(\text{ASD})$$

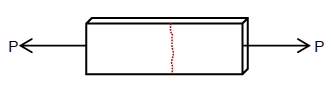
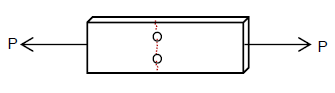
2) Tensile rupture in the net section

$$P_n = F_u A_e$$ $$\phi = 0.75 \;(\text{LRFD}), \quad \Omega = 2.00 \;(\text{ASD})$$

Effective Net Area

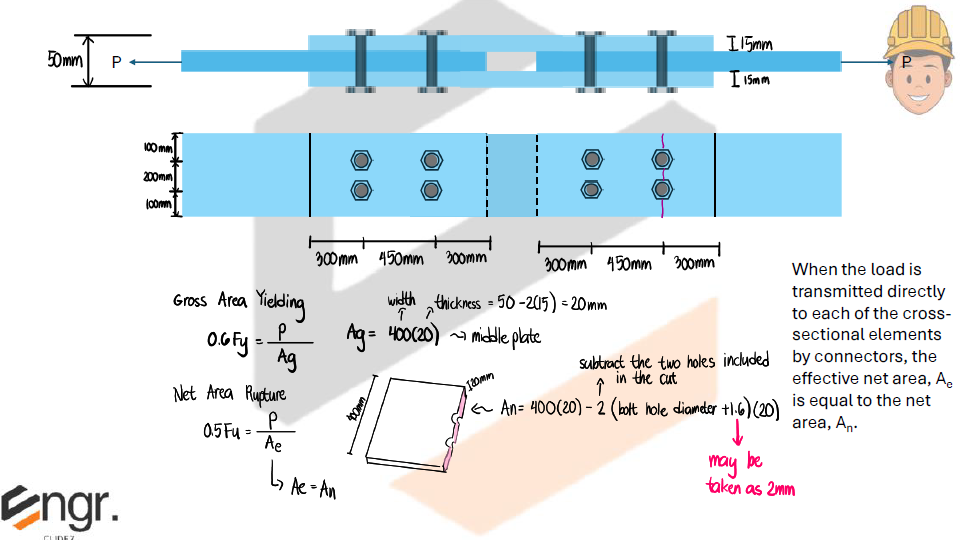
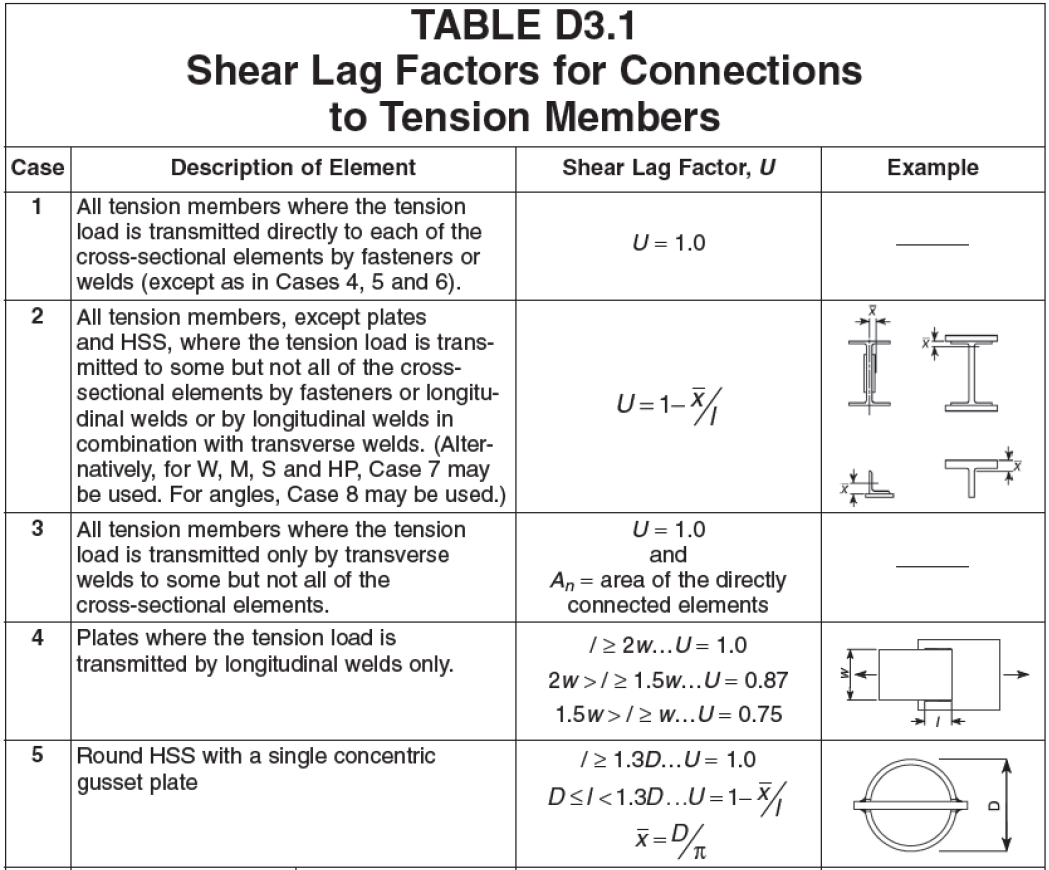
The effective area of tension members shall be determined as:

$$A_e = A_n \, U$$

where: $U$ = shear lag factor
$A_n=A_g-A_h; A_n\le 0.85A_g$ for design of splice plates with holes.

Standard Hole Adjustment — If the nominal hole diameter is given, add:
1.6 mm (2001) or 2 mm (2010/2015) to obtain the effective/standard hole diameter.

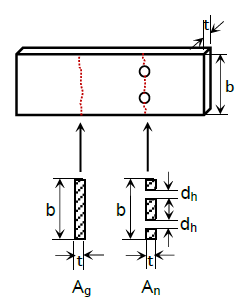
The figure of the cross section at the left describes the gross area, while that on the right illustrates the net area. The net area subtracts the area of the holes from the gross area.

Block Shear Strength

$$R_n = 0.6\,F_u A_{nv} + U_{bs} F_u A_{nt} \;\;\le\;\; 0.6\,F_y A_{gv} + U_{bs} F_u A_{gt}$$ $$\phi = 0.75 \;(\text{LRFD}), \quad \Omega = 2.00 \;(\text{ASD})$$

Sample Area Computations

Strength of Fillet Welds

$$R_n = 0.60\,F_{exx}\,(0.707\,t\,L)$$ $$\phi = 0.75 \;(\text{LRFD}), \quad \Omega = 2.00 \;(\text{ASD})$$

CE Board Exam Randomizer