Staggered Fasteners

In tension member connections with bolts, the net area is largest when fasteners are placed in a single line. However, space constraints often require multiple rows of bolts. To reduce the loss of cross-sectional area, bolts can be arranged in a staggered pattern, where holes do not line up directly. This arrangement ensures that any potential failure plane passes through fewer bolt holes, helping maintain strength and efficiency compared to non-staggered layouts.

Staggered Connection Figures

Cochrane's Formula for Staggered Connections with Uniform Thickness

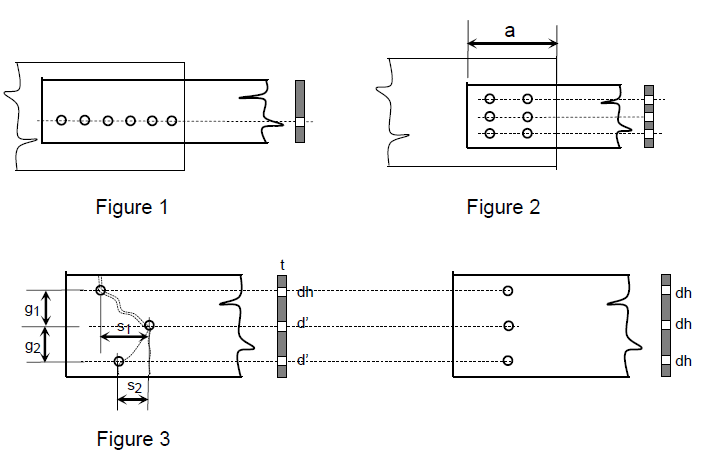
Cochrane (1922) proposed that when deducting the area corresponding to a staggered hole, a reduced diameter d′ should be used, given by:

$$ d' = d_h - \frac{s^2}{4g} $$

The net width, b_n, is then:

$$ b_n = b - \Sigma d' $$

$$ b_n = b - \Sigma \left( d_h - \frac{s^2}{4g} \right) $$

The net area, A_n, is:

$$ A_n = t(b_n) $$

$$ A_n = t \left( b - \Sigma d_h + \Sigma \frac{s^2}{4g} \right) \quad \text{for uniform thickness} $$

Where:
s = pitch (horizontal distance between adjacent bolts)
g = gauge (vertical distance between adjacent bolts)
d_h = diameter of hole

Cochrane's Formula for Staggered Connections with Non-Uniform Thickness

The tension member below illustrates a connection in which holes are made on different elements with different thicknesses.

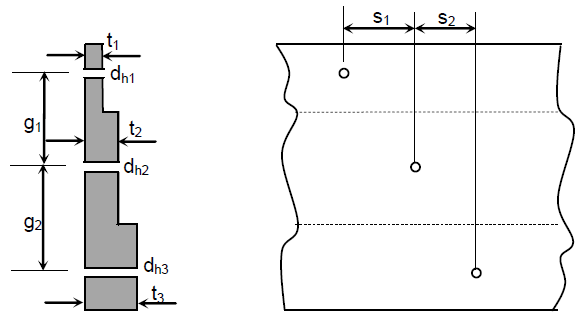The equation of the net area becomes:

$$ A_n = A_g - t_1(d_{h1}) - t_2 \left( d_{h2}-\frac{s_1^2}{4g_1} \right) - t_3 \left( d_{h3}-\frac{s_2^2}{4g_2} \right) $$