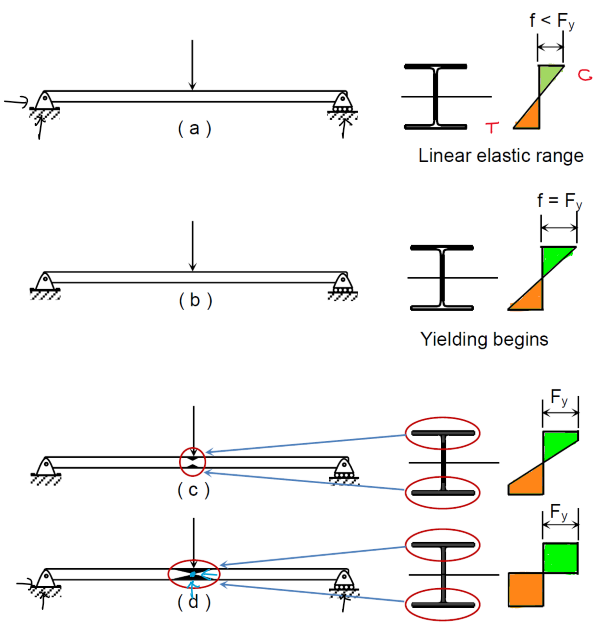
When all elements of the beam's cross-section have yielded, any further increase in load will cause collapse. At this stage, the beam has reached the yield plateau of the stress→strain curve, and unrestricted plastic flow will occur. A plastic hinge forms, and together with the actual hinges at the beam ends, they constitute an unstable mechanism.
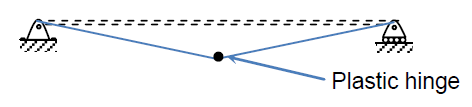
Structural analysis based on collapse mechanism is called plastic analysis. This method applies the principle of virtual work, where an assumed mechanism is subjected to virtual displacements consistent with the mechanism's motion, and the external work is equated to the internal work.
Before solving plastic analysis problems, recall some principles of the virtual work method:
External Work:
Internal Work:

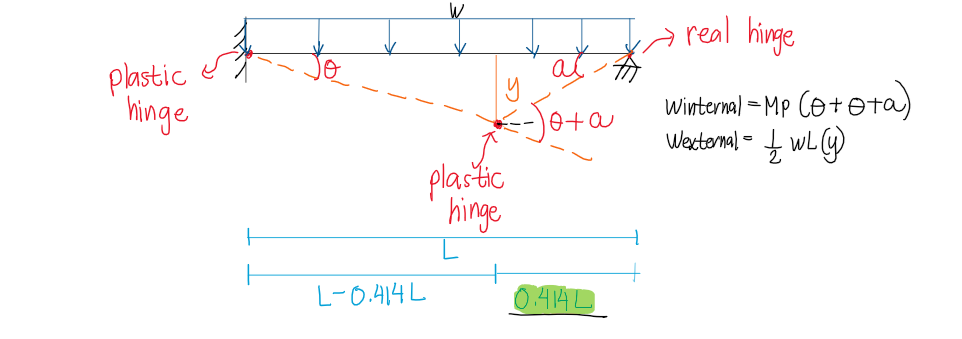
Recall:
When all the elements of the cross-section of the beam has yielded, any further increase in the load will cause collapse, since all elements of the cross-section reached the yield plateau of the stress-strain curve and unrestricted plastic flow will occur.





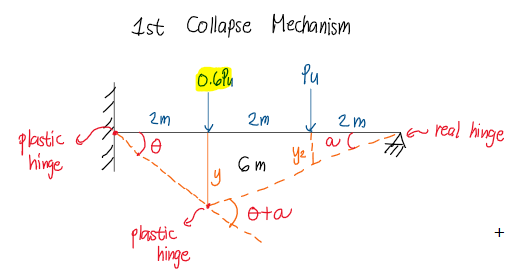
A propped beam having a span of 6m carries two concentrated loads of 0.6Pu and Pu at its middle thirds. The beam has a plastic section modulus of 1852x103mm3. Fy=248MPa. Determine the value of Pu so that the beam is about to collapse.
A. 324kN
B. 353kN
C. 422kN
D. 521kN



 $$ \frac{y}{4} = \frac{y_2}{2} $$
$$ y_2 = \frac{2}{4}y $$
$$ y_2 = 0.5y $$
$$ 2\theta = 4\alpha $$
$$ \alpha = \frac{2}{4}\theta $$
$$ \alpha = 0.5\theta $$
$$ \tan\theta = \frac{y}{2} $$
$$ 2\theta = y $$
$W_{ext} = W_{int}$
$ 0.6P_u(y) + P_u(0.5y) = M_p(\theta + \theta + \theta_a) $
$$ \frac{y}{4} = \frac{y_2}{2} $$
$$ y_2 = \frac{2}{4}y $$
$$ y_2 = 0.5y $$
$$ 2\theta = 4\alpha $$
$$ \alpha = \frac{2}{4}\theta $$
$$ \alpha = 0.5\theta $$
$$ \tan\theta = \frac{y}{2} $$
$$ 2\theta = y $$
$W_{ext} = W_{int}$
$ 0.6P_u(y) + P_u(0.5y) = M_p(\theta + \theta + \theta_a) $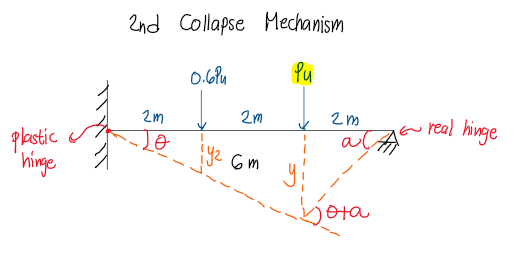 $$\frac {y}{4}=\frac {y_2}{2}$$
$$y_2=0.5y$$
$$2\alpha=4\theta$$
$$\alpha=2\theta$$
Therefore, $$y=4\theta$$
$W_{ext} = W_{int}$
$$\frac {y}{4}=\frac {y_2}{2}$$
$$y_2=0.5y$$
$$2\alpha=4\theta$$
$$\alpha=2\theta$$
Therefore, $$y=4\theta$$
$W_{ext} = W_{int}$ 
