Compression Members

Compression members are elements that carry primarily axial compressive forces. The most common example in buildings and bridges is the column (wooden versions are often called posts). Shorter or non-column members in compression may be called struts or compression blocks; bracing at column and roof joints can also resist compression. Some truss members act in compression.

The actual (applied) compressive stress is:

$$ f_a=\frac{P}{A} $$

Euler’s Column Theory

For a long, slender member loaded axially, a gradually increased load will eventually cause instability and lateral deflection—buckling. The corresponding load is the critical buckling load. If the member is stockier, a larger load is needed to reach instability; extremely stocky members may fail by compressive yielding instead of buckling.

Buckling strength depends on slenderness. Euler’s critical load is:

$$ P_{cr}=\frac{\pi^2 E I}{L^2} $$

Expressed using slenderness ratio $L/r$:

$$ P_{cr}=\frac{\pi^2 E A}{(L/r)^2} $$

The corresponding critical buckling stress is:

$$ F_{cr}=\frac{\pi^2 E}{(L/r)^2} $$

Limitations of Euler’s Formula

If $P/A$ exceeds the proportional limit of the material, Euler’s formula is not applicable.
If $L/r < 100$, Euler’s formula is invalid; the proportional limit then controls the critical stress $P/A$.

Inelastic Buckling (Tangent Modulus)

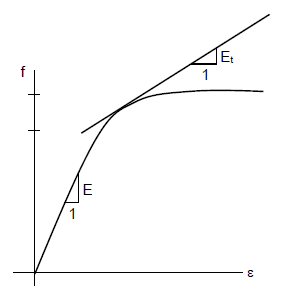
When the stress at buckling is above the proportional limit, the stress–strain curve is nonlinear and the elastic modulus $E$ is no longer appropriate. Replacing $E$ with the tangent modulus $E_t$ gives the inelastic buckling load:

$$ P_{cr}=\frac{\pi^2 E_t I}{L^2} $$

Here, $E_t$ is the slope of the stress–strain curve between the proportional limit $F_{pl}$ and yield strength $F_y$.

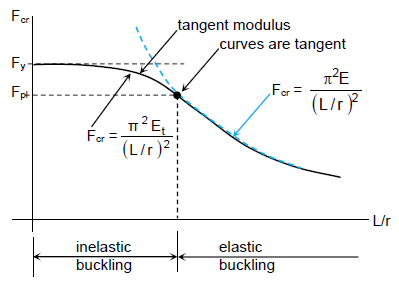
The column strength curve depicts the compressive strength of a column for a given material. Aside from the material properties $F_y$, $E$, and $E_t$, the strength depends primarily on the slenderness ratio $L/r$.

Summary of Formulas

Slenderness Ratio (SR)

$$ SR = \frac{kL}{r} $$

Euler’s Critical Buckling Load

$$ P_{cr} = \frac{\pi^2 E I}{(k\cdot L)^2} $$

Euler’s Critical Buckling Stress

$$ F_{cr} = \frac{\pi^2 E}{(SR)^2} $$

Effective Length Factors

Old Code

A column is a compression member that is relatively slender compared to its length. Such members usually fail by buckling rather than crushing. Columns are generally classified into three groups:

1. Short Columns:
Failure occurs mainly by crushing, with no buckling involved.

2. Intermediate Columns:
Some fibers reach the yield stress, causing failure through a combination of crushing and buckling. This type of behavior is considered elastic.

3. Long Columns:
Long columns usually buckle elastically, as their axial buckling stress remains below the proportional limit. They typically fail by buckling or lateral bending. The longer the column, the more prone it is to buckle, and the smaller the load it can support. Buckling tendency is measured by the slenderness ratio, which is the ratio of the column length to its least radius of gyration. Higher slenderness ratios correspond to lower load-carrying capacity.

Capacity of a Column

The axial capacity of a column is given by:

$$ P = F_a A $$

Where:
$A$ = cross-sectional area of the column
$F_a$ = allowable compressive stress

Critical Buckling Load

$$ P_c = \frac{\pi^2 E I}{(K L_u)^2} $$

NSCP Formulas for Axially Loaded Columns

1. When $KL/r < C_c$ (Intermediate Column)

For axially loaded compression members with unbraced length ratios less than $C_c$, the allowable stress is:

$$ F_a = \left[1 - \frac{(KL/r)^2}{2C_c^2}\right] \frac{F_y}{F.S.} $$

Where:

$$ C_c = \sqrt{\frac{2 \pi^2 E}{F_y}} $$

Factor of safety:

$$ F.S. = \frac{5}{3} + \frac{3(KL/r)}{8C_c} - \frac{(KL/r)^3}{8C_c^3} $$

2. When $KL/r > C_c$ (Long Column)

For slender columns where the slenderness ratio exceeds $C_c$, the allowable compressive stress is:

$$ F_a = \frac{12 \pi^2 E}{23 (KL/r)^2} $$

This is Euler’s formula with a factor of safety of $\tfrac{23}{12} \approx 1.92$.

Definitions:

$K$ = effective length factor
$P$ = allowable axial load
$A$ = cross-sectional area
$F_a$ = allowable compressive stress
$P = F_a A$

In the Civil Engineering Board Exam, the following table is usually provided, where we only have to consult the values of kL/r provided and their corresponding F_a.

NSCP 2015 (ASD & LRFD) — Section 505: Design of Members for Compression

Design Compressive Strength

$$ \phi_c P_n \quad \text{(LRFD)} \qquad \Omega_c P_n \quad \text{(ASD)} $$

Where: $\phi_c = 0.9$ (LRFD), $\Omega_c = 1.67$ (ASD).

505.3 Compressive Strength of Flexural Buckling of Members Without Slender Elements

The nominal compressive strength, $P_n$, is based on the limit state of flexural buckling:

$$ P_n = F_{cr} A_g \qquad (505.3-1) $$

The flexural buckling stress, $F_{cr}$, is determined as follows:

When
$$ \frac{kL}{r} \leq 4.71 \sqrt{\frac{E}{F_y}} \quad \text{or} \quad (F_e \geq 0.44 F_y) $$

$$ F_{cr} = \left[0.658^{\,F_y/F_e}\right] F_y \qquad (505.3-2) $$
When
$$ \frac{kL}{r} > 4.71 \sqrt{\frac{E}{F_y}} \quad \text{or} \quad (F_e < 0.44 F_y) $$

$$ F_{cr} = 0.877 F_e \qquad (505.3-3) $$

Where:

$F_e$ = elastic critical buckling stress, determined from:

$$ F_e = \frac{\pi^2 E}{(KL/r)^2} \qquad (505.3-4) $$

502.8.1 Note: For members designed in compression, the slenderness ratio $kL/r$ should preferably not exceed 200. If this limit is exceeded, the allowable stress must not exceed the value obtained from Equation (505-2).

Section Properties Important in Compression Members (esp. Built-Up Sections)

A. Gross Area

Total area of the composite section.

B. Moments of Inertia (about centroidal axes)

$$ I_x = I_{xo} + A\,d_y^{\,2} \qquad I_y = I_{yo} + A\,d_x^{\,2} $$

Parallel-axis theorem: $I_{x0}, I_{y0}$ are about each component’s own centroid; $d_x, d_y$ are centroid offsets to the composite centroid.

C. Radii of Gyration

$$ r_x = \sqrt{\frac{I_x}{A}} \qquad r_y = \sqrt{\frac{I_y}{A}} $$

Other Important Properties

A. Elastic Section Moduli

$$ S_x = \frac{I_x}{c_x} \qquad S_y = \frac{I_y}{c_y} $$

$c_x, c_y$ = distances from the neutral axes to the extreme fibers.

B. Polar Moment of Inertia

$$ J = I_x + I_y $$

C. Product of Inertia

$$ I_{xy} = \sum A\,\bar{x}\,\bar{y} $$

$\bar{x}, \bar{y}$ = coordinates of each component area relative to the composite centroidal axes.