Column Base Plate

Unlike the beam bearing plate, column base plates do not consider web yielding or web crippling in design. Instead, the design focuses on bearing pressure on the supporting material (concrete) and bending of the plate itself. This method is referred to as the cantilever method.

a) Bearing on Concrete Support

According to AISC requirements for concrete bearing strength:

• If the plate covers the full support area:

$$ P_p = 0.85 f'_c A_1 $$

• If the plate does not cover the full support area:

$$ P_p = 0.85 f'_c A_1 \sqrt{\frac{A_2}{A_1}} \;\;\le\;\; 1.7 f'_c A_1 $$

Where:

$f'_c$ = compressive strength of concrete
$A_1$ = bearing area (plate area)
$A_2$ = full support area (or largest concentric area similar to $A_1$)

For LRFD: $\phi_c P_p$ with $\phi_c = 0.60$
For ASD: $P_p/\Omega_c$ with $\Omega_c = 2.50$

b) Bending of the Plate

The base plate is subjected to two-way bending. Using the cantilever method, the column load is distributed over an area equal to $0.80b_f$ by $0.95d$. The plate bends over spans $m$, $n$, or $n'$ depending on the critical direction.

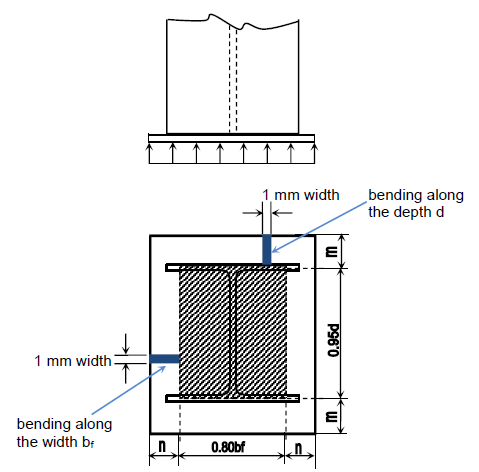
The required thickness $t$ is:

$$ t = \ell \sqrt{\frac{2 P_u}{0.90 B N F_y}} \quad \text{for LRFD} $$

$$ t = \ell \sqrt{\frac{2 P_a}{0.60 B N F_y}} \quad \text{for ASD} $$

where $\ell$ is the largest value of $m$, $n$, or $n'$.

Values of $m$, $n$, and $n'$:

$$ m = \frac{N - 0.95d}{2}, \quad n = \frac{B - 0.80b_f}{2}, \quad n' = \frac{\sqrt{d b_f}}{4} \rightarrow choose\ largest$$

Symbols:
$B$ = plate width
$N$ = plate length
$d$ = column depth
$b_f$ = column flange width
$F_y$ = yield stress of steel
$P_u$, $P_a$ = factored and allowable column loads