Beam Columns

NSCP 2015 (ASD & LRFD) – Section 508: Design of Members for Combined Forces and Torsion

This section covers members subjected to axial force and flexure about one or both axes (with/without torsion) and torsion-only members. For doubly or singly symmetric members:

$$ 0.1 \le \frac{I_{yc}}{I_y} \le 0.9 $$

Interaction concept

Design uses a load–resistance ratio that must not exceed unity:

$$ \frac{\text{required strength}}{\text{available strength}} \le 1.0 $$

When axial compression and bending act together about the $x$ and/or $y$ axes, the corresponding ratios are summed and limited to $1.0$.

508.1.1 Doubly and Singly Symmetric Members in Flexure and Compression

Use the appropriate interaction expression based on $P_r/P_c$:

For $P_r/P_c \ge 0.2$

$$ \frac{P_r}{P_c} + \frac{8}{9}\!\left(\frac{M_{rx}}{M_{cx}} + \frac{M_{ry}}{M_{cy}}\right) \le 1.0 \quad (508.1\!-\!1a) $$

For $P_r/P_c < 0.2$

$$ \frac{P_r}{2P_c} + \left(\frac{M_{rx}}{M_{cx}} + \frac{M_{ry}}{M_{cy}}\right) \le 1.0 \quad (508.1\!-\!1b) $$

Symbols & mapping

$P_r$ = required axial compressive strength (actual load); $P_c$ = available axial compressive strength.
$M_{rx}, M_{ry}$ = required moments about $x$ and $y$; $M_{cx}, M_{cy}$ = available moment capacities about $x$ and $y$.
LRFD available bending uses $\phi_b M_n$; ASD uses $M_n/\Omega_b$ (substitute accordingly when checking the ratios).
$x$ = strong-axis bending; $y$ = weak-axis bending.

Interaction Formulas (NSCP 2015)

For LRFD:

For: $\dfrac{P_u}{\phi_c P_n} \ge 0.20$ $$ \frac{P_u}{\phi_c P_n} + \frac{8}{9}\!\left(\frac{M_{ux}}{\phi_b M_{nx}} + \frac{M_{uy}}{\phi_b M_{ny}}\right) \le 1.0 $$

For: $\dfrac{P_u}{\phi_c P_n} < 0.20$ $$ \frac{P_u}{2\phi_c P_n} + \!\left(\frac{M_{ux}}{\phi_b M_{nx}} + \frac{M_{uy}}{\phi_b M_{ny}}\right) \le 1.0 $$

For ASD:

For: $\dfrac{P_a}{P_n / \Omega_c} \ge 0.20$ $$ \frac{P_u}{P_n / \Omega_c} + \frac{8}{9}\!\left(\frac{M_{ax}}{M_{nx}/\Omega_b} + \frac{M_{ay}}{M_{ny}/\Omega_b}\right) \le 1.0 $$

For: $\dfrac{P_a}{P_n / \Omega_c} < 0.20$ $$ \frac{P_u}{2(P_n / \Omega_c)} + \!\left(\frac{M_{ax}}{M_{nx}/\Omega_b} + \frac{M_{ay}}{M_{ny}/\Omega_b}\right) \le 1.0 $$

Second-order effects / Moment amplification

$$ M_r = B_1 M_{nt} + B_2 M_{lt} $$

$M_{nt}$ = maximum first-order moment assuming no sidesway (braced behavior).
$M_{lt}$ = maximum first-order moment when sidesway occurs (unbraced behavior).
$B_1$ = Amplification factor for moments in members with no sidesway
$B_2$ = Amplification factor for moments in members resulting from sidesway

Braced frames:

$$ B_1 = \frac{C_m}{1 - \alpha\,\dfrac{P_r}{P_{e1}}} \;\;\ge 1.0, \qquad P_{e1}=\frac{\pi^2 E I}{(K_1 L_1)^2} $$

$$ P_r = P_{nt} + B_2 P_{\ell t} $$

Where:

$P_{nt}$ = axial load corresponding to the braced condition
$P_{tt}$ = axial load corresponding to the sidesway condition

As an approximation:

$$ P_r = P_{nt} + P_{\ell t} $$

Unbraced frames:

$$ B_2 = \frac{1}{1 - \dfrac{P_{\text{story}}}{P_{e\,\text{story}}}} $$

Column curvature coefficient, $C_m$

a) Frames subjected to joint translation (sidesway):
$$ C_m = 0.85 $$
b) Braced against joint translation and not subjected to transverse loads between supports:
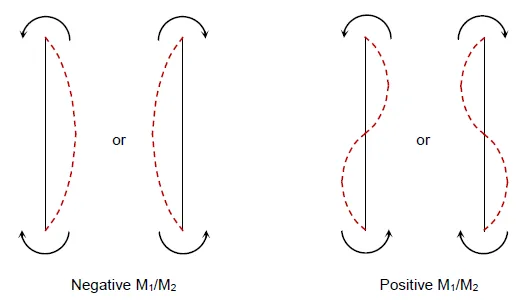
$$ C_m = 0.6 - 0.4\!\left(\frac{M_1}{M_2}\right) $$
where $M_1/M_2$ is the ratio of the smaller to larger end moments in the plane of bending (positive for reverse curvature, negative for single curvature).

c) Braced against joint translation with transverse loading between supports:
- Ends restrained against rotation in the plane of bending:
  $$ C_m = 0.85 $$
- Ends unrestrained against rotation:
  $$ C_m = 1.0 $$