Beam Bearing Plate

Beam Bearing Plate and Column Base Plate

Plates distribute concentrated loads to the supporting material. A beam transfers its reaction to a supporting wall or to the top flange of a girder, while a column transfers its load to a concrete pedestal. Below is a design outline for a beam bearing plate;

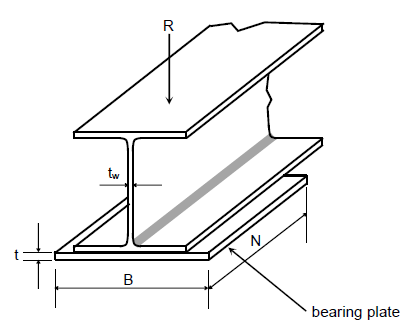
A. Beam Bearing Plate

Designing the bearing plate involves finding its width $B$, length $N$, and thickness $t$ (see figure).

Step 1 — Choose $N$ to prevent web yielding and web crippling

Web yielding. Load spreads through the web at an approximate $1:2.5$ slope. The area in yielding and the nominal strength are:

• At a support:

$$ \text{Area} = (N+2.5k)\,t_w $$

$$ R_n = (N+2.5k)\,F_y\,t_w $$

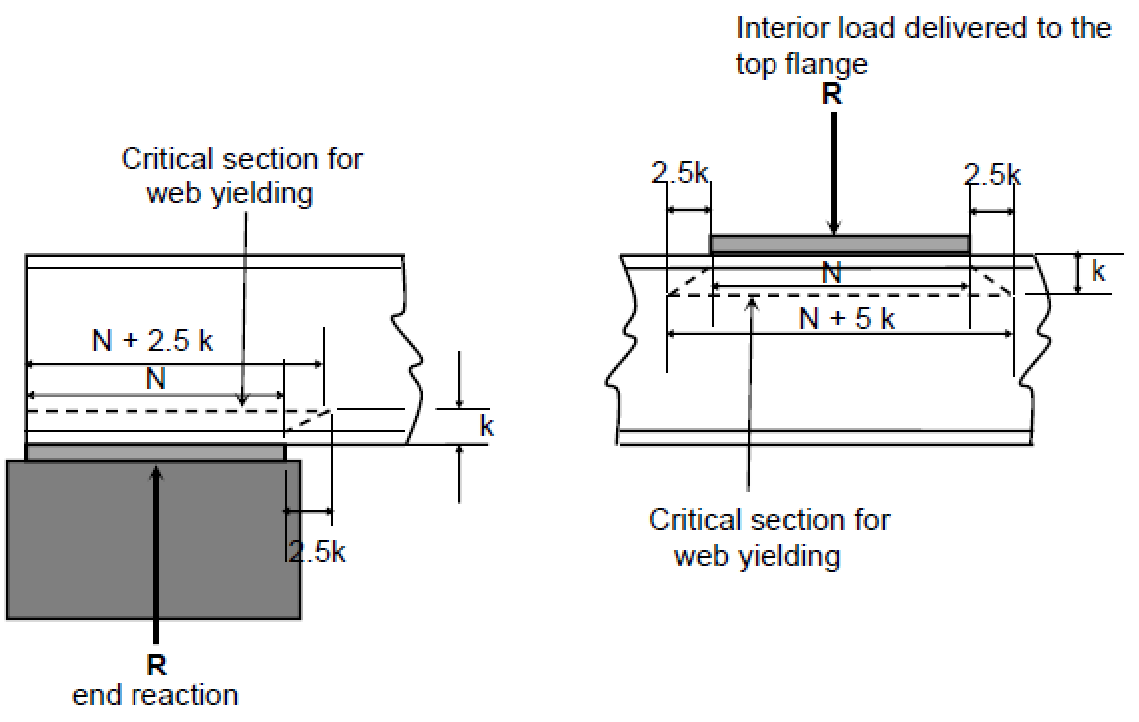
• At an interior load:

$$ \text{Area} = (N+5k)\,t_w $$

$$ R_n = (N+5k)\,F_y\,t_w $$

Design/allowable strengths:

$$ \phi R_n \quad(\phi = 1.00) \qquad \text{or} \qquad \frac{R_n}{\Omega} \quad(\Omega = 1.50) $$

Web Crippling

Buckling of the web caused by concentrated compression through the flange. Use the applicable web-crippling expressions (end reaction and interior reaction); select the case based on whether the load is near the end (within $d/2$) or interior.

For a load at or near the support (within $d/2$ of the end):

• When $N/d \le 0.20$

$$ R_n = 0.40\,t_w^2 \left[\,1 + 3\left(\frac{N}{d}\right)\left(\frac{t_w}{t_f}\right)^{1.5}\right] \sqrt{\frac{E F_y t_f}{t_w}} $$

• When $N/d > 0.20$

$$ R_n = 0.40\,t_w^2 \left[\,1 + \left(\frac{4N}{d} - 0.2\right)\left(\frac{t_w}{t_f}\right)^{1.5}\right] \sqrt{\frac{E F_y t_f}{t_w}} $$

For an interior load, the nominal strength is:

$$ R_n = 0.80\,t_w^2 \left[\,1 + 3\left(\frac{N}{d}\right)\left(\frac{t_w}{t_f}\right)^{1.5}\right] \sqrt{\frac{E F_y t_f}{t_w}} $$

For LRFD, $\phi = 0.75$ and for ASD, $\Omega = 2.00$.

Step 2 — Choose $B$ so concrete (or supporting material) does not crush in bearing

AISC bearing strength for concrete:

• Plate fully covering the support:

$$ P_p = 0.85\,f'_c\,A_1 $$

• Plate not covering the full support:

$$ P_p = 0.85\,f'_c\,A_1 \sqrt{\frac{A_2}{A_1}} \;\;\le\;\; 1.7\,f'_c\,A_1 $$

Where: $f'_c$ = concrete compressive strength;
$A_1$ = bearing area under the plate;
$A_2$ = area of the support geometrically similar and concentric with $A_1$.
Design/allowable:

$$ \phi_c P_p \;(\phi_c = 0.60) \qquad \text{or} \qquad \frac{P_p}{\Omega_c} \;(\Omega_c = 2.50) $$

Step 3 — Choose thickness $t$ for plate bending strength

Treat a $1\,$mm strip of plate as a cantilever of span $n$ (see figure). With uniform pressure $R/(B N)$, the strip bending moment is:

$$ M = \frac{R}{B N}\left(1\right)\!\left(n\right)\!\left(\frac{n}{2}\right) = \frac{R n^2}{2 B N} $$

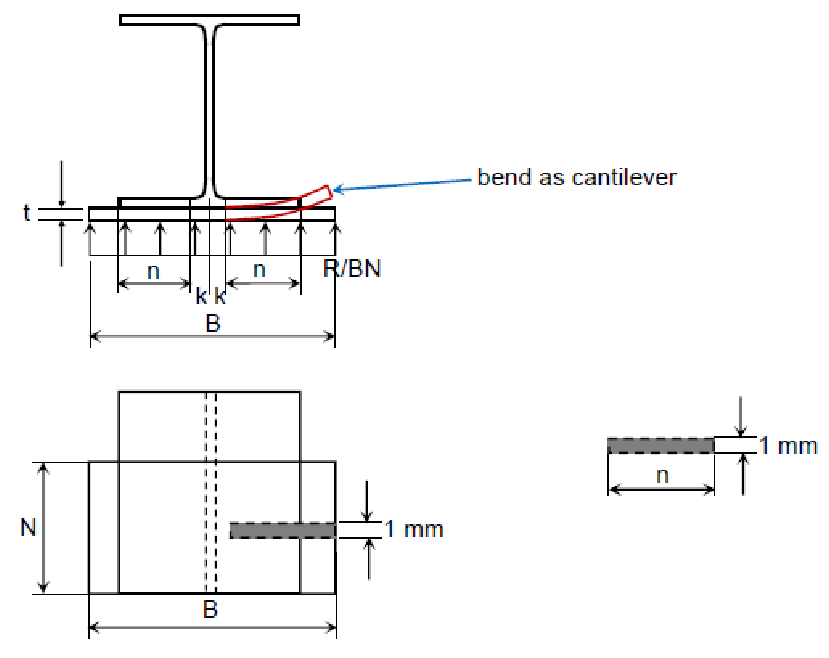
Plastic moment capacity of a rectangular strip of thickness $t$:

$$ M_p = F_y\!\left(t\right)\!\left(1 \cdot \frac{t}{2}\right) = F_y\,\frac{t^2}{4} $$

LRFD thickness. Equate $M_u=\phi_b M_p$ with $\phi_b=0.90$ and solve for $t$:

$$ \frac{R_u n^2}{2 B N} = 0.90\,F_y\,\frac{t^2}{4} \;\;\Rightarrow\;\; t = \sqrt{\frac{2.22\,R_u\,n^2}{B N\,F_y}}. $$

ASD thickness. Equate $M_p/\Omega_b = M_a$ with $\Omega_b=1.67$ and solve for $t$:

$$ \frac{F_y\,t^2}{4\,(1.67)} = \frac{R_a n^2}{2 B N} \;\;\Rightarrow\;\; t = \sqrt{\frac{3.34\,R_a\,n^2}{B N\,F_y}}. $$

Symbols:
$B$ = plate width;
$N$ = plate length (load length);
$t$ = plate thickness;
$t_w$ = web thickness;
$k$ = fillet distance from flange face to web toe;
$d$ = beam depth;
$R_u, R_a$ = factored/allowable reaction;
$F_y$ = steel yield stress;
$E$ = modulus of elasticity;
$\phi, \Omega$ = resistance/safety factors.