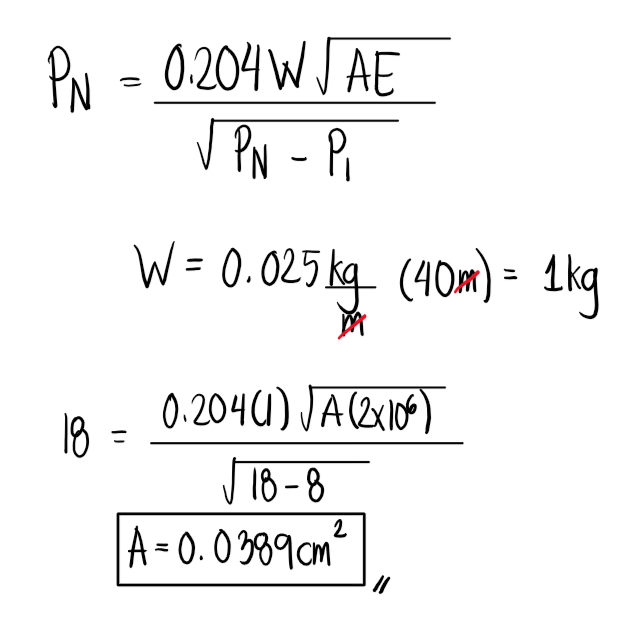Difference Between Measuring and Laying Out
Measuring Distances
This is when you use a tape to determine the length of something that already exists (e.g., the width of a road, distance between two survey points, length of a beam).
→ You record what the tape shows.
Laying Out Distances
This is when you use the tape to set a required length on the ground or structure (e.g., staking 50 m for a building foundation, marking 20 m for a pipeline).
→ You establish the distance based on the tape.
Four measurements of a distance were recorded as 352.45, 352.04, 351.89, and 353.12m., and given weights are 2, 5, 1, and 6, respectively. Determine the weighted mean.



See images:




A student recorded the following repeated paces of a given line: 456, 448, 462, 447, 452, and 455. If his pace factor is 0.628m/pace, what is the approximate length of the line in meters?



$$Ave. Pace = \frac{456+448+462+447+452+455}{6}=453.33 \ paces$$
$$Length\ of\ line = 453.333(0.628)=284.69m$$




A line was determined to be 2395.25m when measured with a 30-m steel tape supported throughout its length under the pull of 4kg at a mean temperature of 35°C. The tape used is of standard length at 20°C under a pull of 5kg. The cross sectional area of the tape is 0.03 sq. cm. Coefficient of thermal expansion is 1.16x10-5/°C. Modulus of elasticity of the tape is 2x106kg/cm2.
a. Determine the error due to change in temperature
b. Determine the error due to tension
c. Determine the corrected length of the line



See images:




CE Board May 2015
A student was asked to measure a 500m long line using a 25m tape that is of standard length at a temperature of 28°C. If the average temperature is 12°C, what is the required measurement? α=0.0000116m/m°C



See images:




CE Board May 2016
A student was asked to make a 345.43m long line using a 25m tape that is 0.0021m too long. What is the required measurement?



See images:




A steel tape is 100 meters long at a standard pull of 65N. Compute the pull correction in mm if during measurement the applied pull is 40N. The tape has a cross-sectional area of 3.18mm2 and a modulus of elasticity E=200,000MPa.



See images:




A steel tape is 100m long at a temperature of 20°C and a pull of 10kg. It was used to measure a distance of 624.95m at a temperature of 32°C with an applied pull of 15kg during measurement with the tape supported at both ends. Coefficient of thermal expansion is 0.0000116/°C and a modulus of elasticity of 2x106kg/cm2. The weight of the tape is 0.04kg/m and has a cross-sectional area of 0.06cm2
a. Compute the sag correction
b. Compute the total correction for tension, sag, and temperature.
c. Compute the corrected length of the line.



See images:




A civil engineer used a 30m tape in measuring an inclined distance. The measured length on the slope was recorded to be 459.20m long. The difference in elevation between the initial point and the end point was found to be 1.25m. The 30m tape is of standard length at a temperature of 10°C and a pull of 50N. During measurement, the temperature reading was 15°C and the tape was supported at both ends with an applied pull of 75N. The cross-sectional area of the tape is 6.50mm2 and the modulus of elasticity is 200GPa. The tape has a mass of 0.075kg/m. K=0.0000116/°C.
a. Determine the total correction per tape length.
b. Determine the correction for slope.
c. Determine the corrected horizontal distance.



See images:




Compute the normal tension which will be applied to a tape supported over two supports in order to make the tape equal to its nominal length when supported only at end points. The steel tape is 30m long and weighs 0.84kg when supported throughout its length under a standard pull of 5.6kg, with the modulus of elasiticity of 2x106kg/cm2 and an area of 0.06cm2



See images:
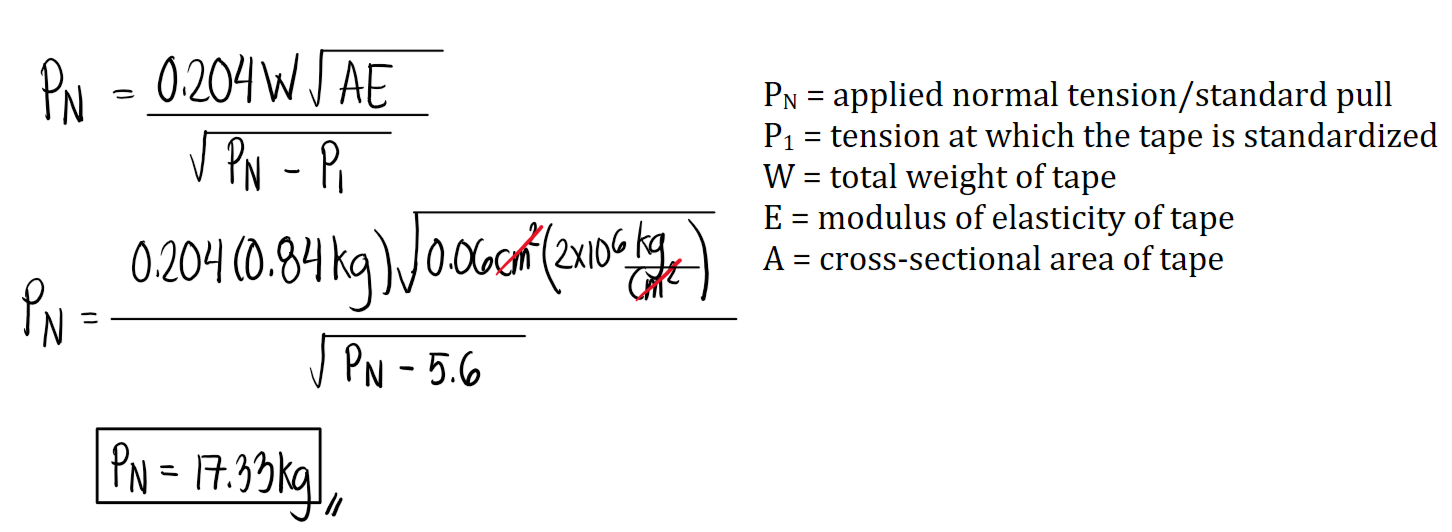



A line 100m long was paced by a surveyor for four times with the following data: 142, 145, 145.5, and 146. Then, another line was paced for four times again with the following results: 790, 790.5, 789.5 and 791. Determine the distance of the new line.



Given: Calibration line = 100 m. Paces on 100 m: 142, 145, 145.5, 146. New line paces: 790, 790.5, 789.5, 791.
1) Average paces on the 100 m calibration line
2) Average paces on the new line
3) Pace length (meters per pace)
4) Distance of the new line
Answer: The distance of the new line is ≈ 546.41 m (say, 546.4 m).




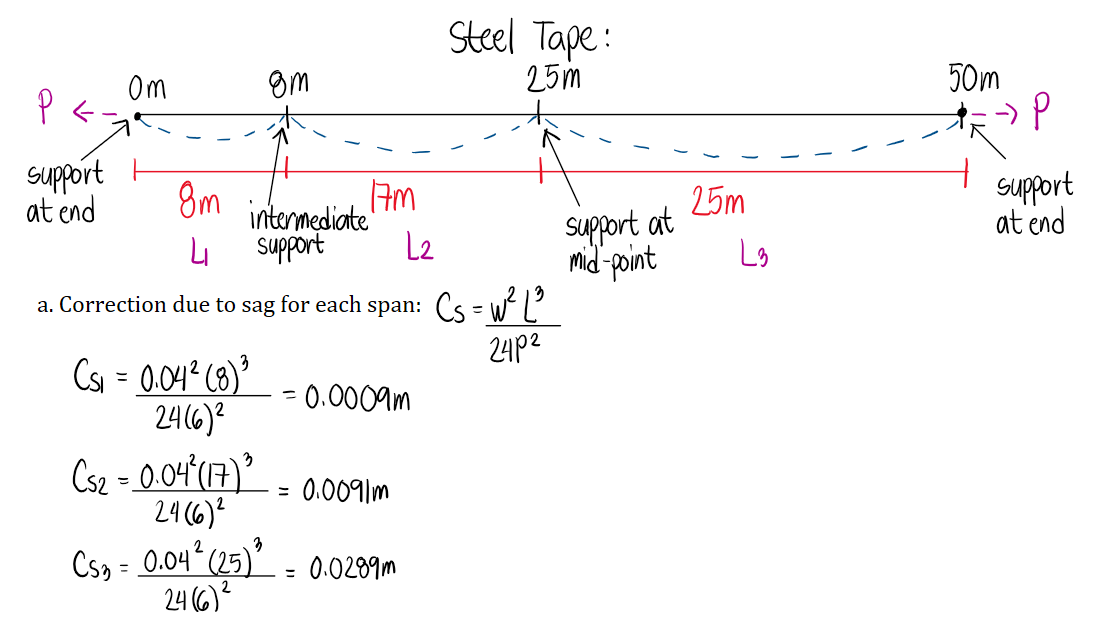
A 50-m steel tape weighs 0.04kg/m and is supported at its end points and at the 8-m and 25-m marks. If a pull of 6kg is applied, determine the following:
a. Correction due to sag between the 0m and 8-m marks, 8-m and 25-m marks, and the 25-m and 50-m marks.
b. Correction due to sag for one tape length.
c. Corrected distance between the ends of the tape.
d. If a 500m distance has been measured using such tape and support conditions, determine the corrected measurement.



See images:



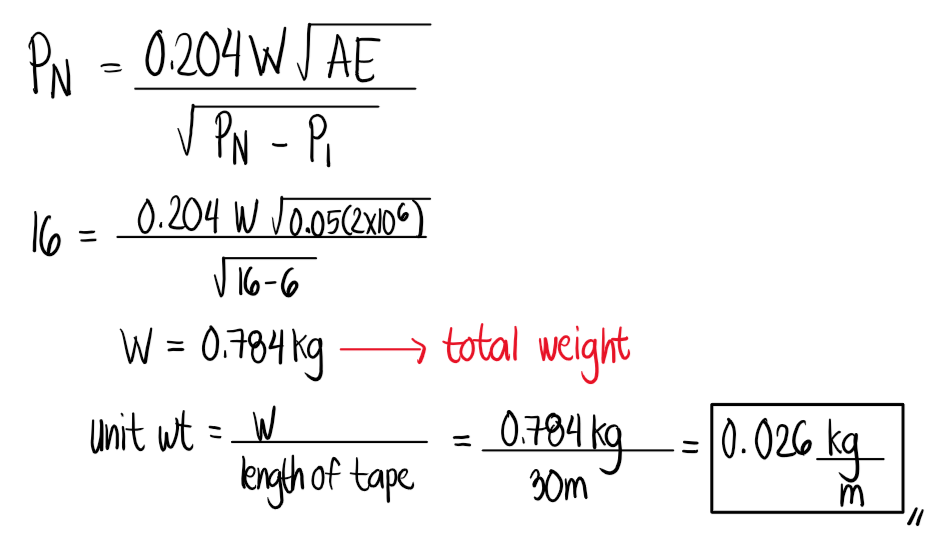
A steel tape is 30m long under a standard pull of 6kg with a constant cross-sectional area of 0.05cm2. If the normal tension applied to make the tape equal to its nominal length when supported only at the end points, that is the effect of sag will be eliminated by the elongation of the tape due to the application of this load is equal to 16kg, determine the unit weight of the tape. Modulus of elasticity of the tape is 2x106kg/cm2.
See images:
Under a standard pull of 8kg, the steel tape is 40m long. A normal tension of 16kg makes the elongation of the tape offset the effect of sag. If the tape weighs 0.025kg/m, and E=2x106kg/cm2, determine its cross-sectional area in sq. cm.
See images: