Surveying is the science of determining the earth’s dimensions and surface form by measuring distances, directions, and elevations. It also covers staking out lines/grades for construction and the computation of areas, volumes, and related quantities for preparing maps and diagrams.
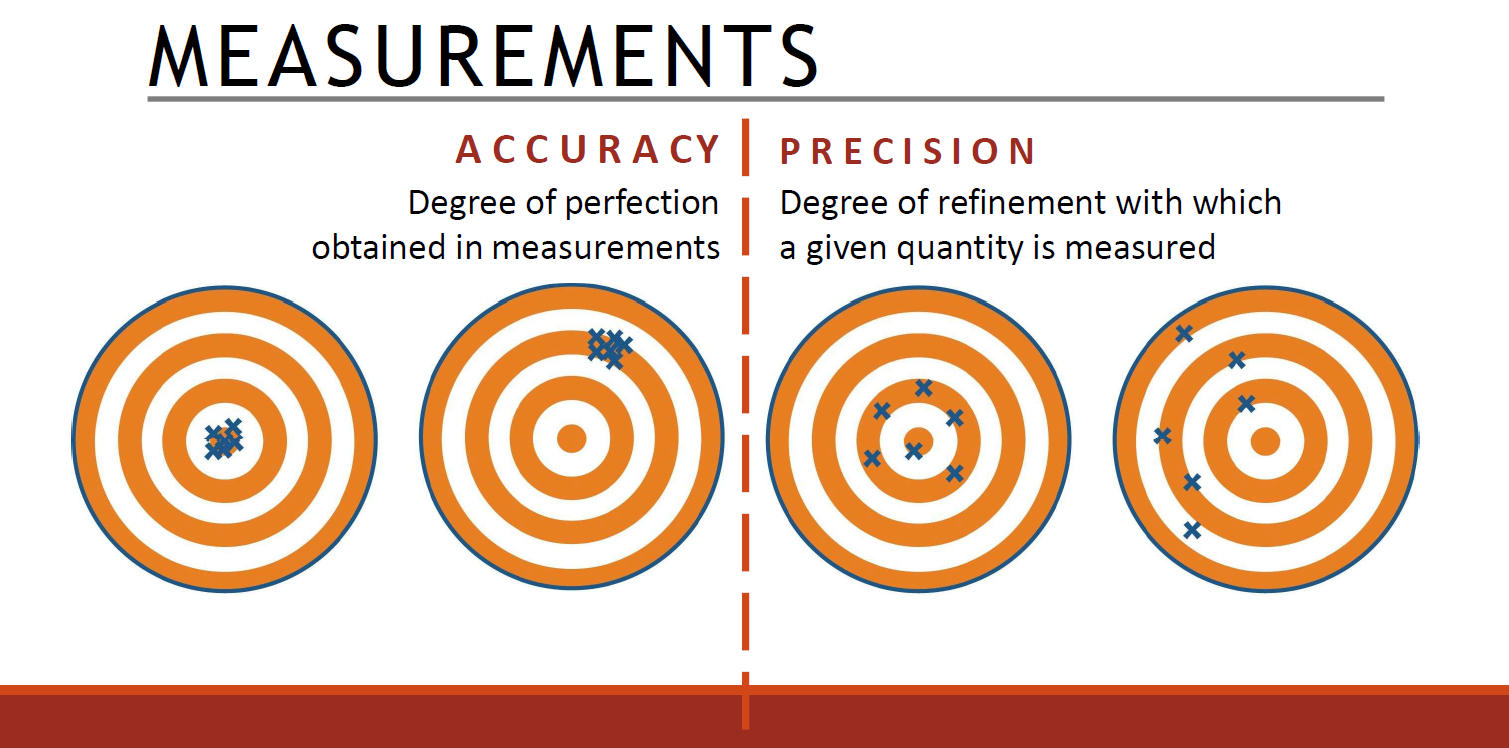
Measurement is central to surveying, but no measurement is exact; the true value is never fully known. Accuracy = closeness to the true value (degree of perfection), while Precision = repeatability or refinement of readings.
835.82 ± 0.06
The quality of a measurement can be expressed by stating a relative error.
Maximum Probable Value: 835.88ft
Minimum Probable Value: 835.76ft
Most Probable Value: 835.82ft
Probable error statements:
50% error: “There is a 50% chance that the error is ±0.12 ft or less and a
50% chance that it contains a larger error”
90% error: “There is a 90% chance that the error is ±0.12 ft or less and a 10%
chance that it contains a larger error”
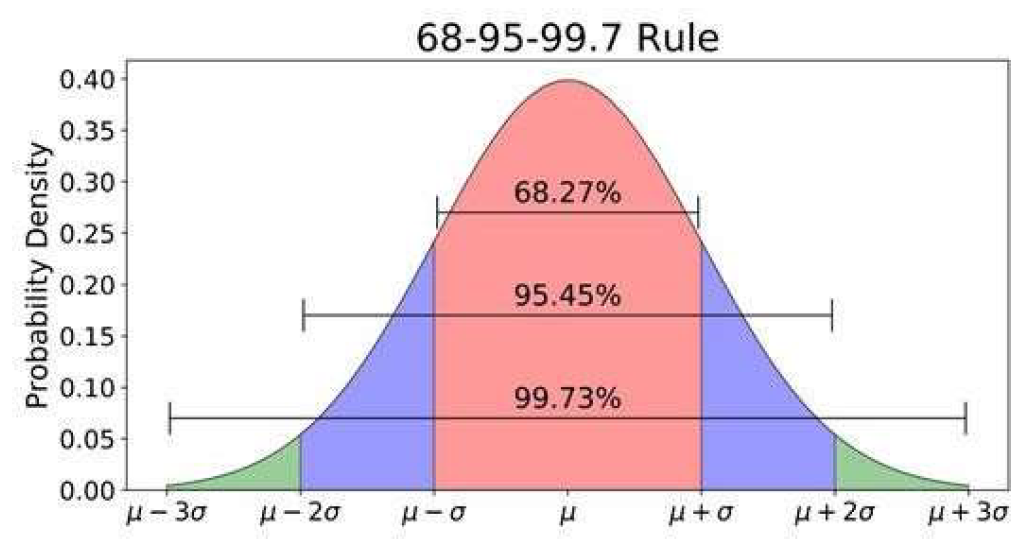
Error of a Series of Similar Measurements
When a series of quantities are measured, random errors tend to accumulate in proportion to the square root of the number of measurements. Error grows with the square root of the count:
$E_{\text{series}}=\pm E\sqrt{n}$, where $E$ is the error of each observation.
If a distance is measured a number of times with a probable random
error in each measurement, the probable error in the distance will
equal the total probable error in the number of observations divided by
the number of observations.
Error of the mean (standard error): $E_{\bar{x}}=\dfrac{E_{\text{series}}}{n}=\pm\dfrac{E\sqrt{n}}{{n}}$
Combine independent probable errors in quadrature:
$E_{\text{total}}=\pm\sqrt{E_1^2+E_2^2+\cdots+E_n^2}$
where $E_p$ = error for probability $p$;
$C_p$ = constant for probability $p$;
$v$ = residuals $\,\big(v_i = x_i-\bar{x}\big)$;
$n$ = number of observations.
| Error (=) | Probability (%) | Probability that error is larger than value |
|---|---|---|
| $0.50\sigma$ | 38.3 | $\approx$ 2 in 3 |
| $0.6745\sigma$ | 50.0 | 1 in 2 |
| $1.00\sigma$ | 68.3 | 1 in 3 |
| $1.6449\sigma$ | 90.0 | 1 in 10 |
| $1.9599\sigma$ | 95.0 | 1 in 20 |
| $2.00\sigma$ | 95.4 | 1 in 23 |
| $3.00\sigma$ | 99.7 | 1 in 333 |
| $3.29\sigma$ | 99.9 | 1 in 1000 |
| Measurement, x (ft) | No. of frequency | Residual or deviation, v = x − μ | v² |
|---|---|---|---|
| 96.9 | 1 | ||
| 96.91 | 2 | ||
| 96.92 | 3 | ||
| 96.93 | 5 | ||
| 96.94 | 6 | ||
| 96.95 | 5 | ||
| 96.96 | 3 | ||
| 96.97 | 2 | ||
| 96.98 | 1 |
Given (from frequency table): total count n = 28
\[ \mu \;=\; \frac{\sum (x_i\,f_i)}{\sum f_i} \;=\; \frac{96.90(1)+96.91(2)+\cdots+96.98(1)}{28} \;=\; \boxed{96.94\ \text{ft}} \]
| Measurement, x (ft) | No. of frequency, f | Residual $v = x-\mu$ (ft) | $v^{2}$ (ft²) |
|---|---|---|---|
| 96.90 | 1 | -0.04 | 0.0016 |
| 96.91 | 2 | -0.03 | 0.0009 |
| 96.92 | 3 | -0.02 | 0.0004 |
| 96.93 | 5 | -0.01 | 0.0001 |
| 96.94 | 6 | 0.00 | 0.0000 |
| 96.95 | 5 | +0.01 | 0.0001 |
| 96.96 | 3 | +0.02 | 0.0004 |
| 96.97 | 2 | +0.03 | 0.0009 |
| 96.98 | 1 | +0.04 | 0.0016 |
| Totals | 28 | $\Sigma \,v^{2} = 0.0102$ |
Sample standard deviation: \[ \sigma \;=\; \sqrt{\frac{\sum\,v^{2}}{n-1}} \;=\; \sqrt{\frac{0.0102}{27}} \;=\; \boxed{0.01944\ \text{ft}} \]
Note: Use $n-1$ (sample SD) when the true mean is unknown.
Determine the 90% error for the distance measurements in ft: 152.93, 153.01, 152.87, 152.98, 152.78, and 152.89.
Given measurements (n = 6): 152.93, 153.01, 152.87, 152.98, 152.78, 152.89
Mean:
$\mu = \frac{152.93 + 153.01 + 152.87 + 152.98 + 152.78 + 152.89}{6}
= \frac{917.46}{6}
= 152.91\ \text{ft}$
| Measurement, x (ft) | Residual $v = x-\mu$ (ft) | $v^2$ (ft²) |
|---|---|---|
| 152.93 | +0.02 | 0.0004 |
| 153.01 | +0.10 | 0.0100 |
| 152.87 | -0.04 | 0.0016 |
| 152.98 | +0.07 | 0.0049 |
| 152.78 | -0.13 | 0.0169 |
| 152.89 | -0.02 | 0.0004 |
| Totals | $\sum v^2 = 0.0342$ |
Sample standard deviation:
$\sigma = \sqrt{\frac{\sum v^2}{n-1}}
= \sqrt{\frac{0.0342}{5}}
= \sqrt{0.00684}
= 0.08268\ \text{ft}$
90% probable error: Using $C_{90\%} = 1.6449$,
$E_{90\%} = C_p \times \sigma
= 1.6449 \times 0.08268
= 0.136\ \text{ft}$
Interpretation: The most probable value is $152.91 \pm 0.136\ \text{ft}$ at 90% confidence, meaning the true value is likely between $152.774\ \text{ft}$ and $153.046\ \text{ft}$.
A series of 12 angles was measured, each angles with an estimated error of ±20 seconds of arc. What is the total estimated error in the 12 angles?
Given:
Number of measurements: $n = 12$
Error in each measurement: $E = \pm 20''$
Formula:
$E_{\text{series}} = \pm E \sqrt{n}$
Substitute values:
$E_{\text{series}} = \pm 20'' \sqrt{12}$
$E_{\text{series}} = \pm 20'' \times 3.4641$
$E_{\text{series}} = \pm 69.28''$
Interpretation: The total estimated error for the 12 angles is $\pm 69.28''$ (about $\pm 1'$ 9.28"), meaning that the accumulated random error across all measurements is larger than the error in a single measurement due to the square root accumulation rule.
The four approximately equal sides of a tract of land were measured. These measurements included the following probable errors: ±0.09 ft, ±0.013 ft, ±0.18 ft, and ±0.40 ft, respectively. Determine the probable error for the total length or perimeter of the tract.
Given:
$E_1 = \pm 0.09\ \text{ft}$
$E_2 = \pm 0.013\ \text{ft}$
$E_3 = \pm 0.18\ \text{ft}$
$E_4 = \pm 0.40\ \text{ft}$
Formula:
$E_{\text{total}} = \pm \sqrt{E_1^2 + E_2^2 + E_3^2 + E_4^2}$
Substitute values:
$E_{\text{total}} = \pm \sqrt{(0.09)^2 + (0.013)^2 + (0.18)^2 + (0.40)^2}$
$E_{\text{total}} = \pm \sqrt{0.0081 + 0.000169 + 0.0324 + 0.16}$
$E_{\text{total}} = \pm \sqrt{0.200669}$
$E_{\text{total}} \approx \pm 0.4485\ \text{ft}$
Interpretation: The probable error for the total length (perimeter) of the tract is approximately $\pm 0.45\ \text{ft}$.
CE Board Exam May 2019
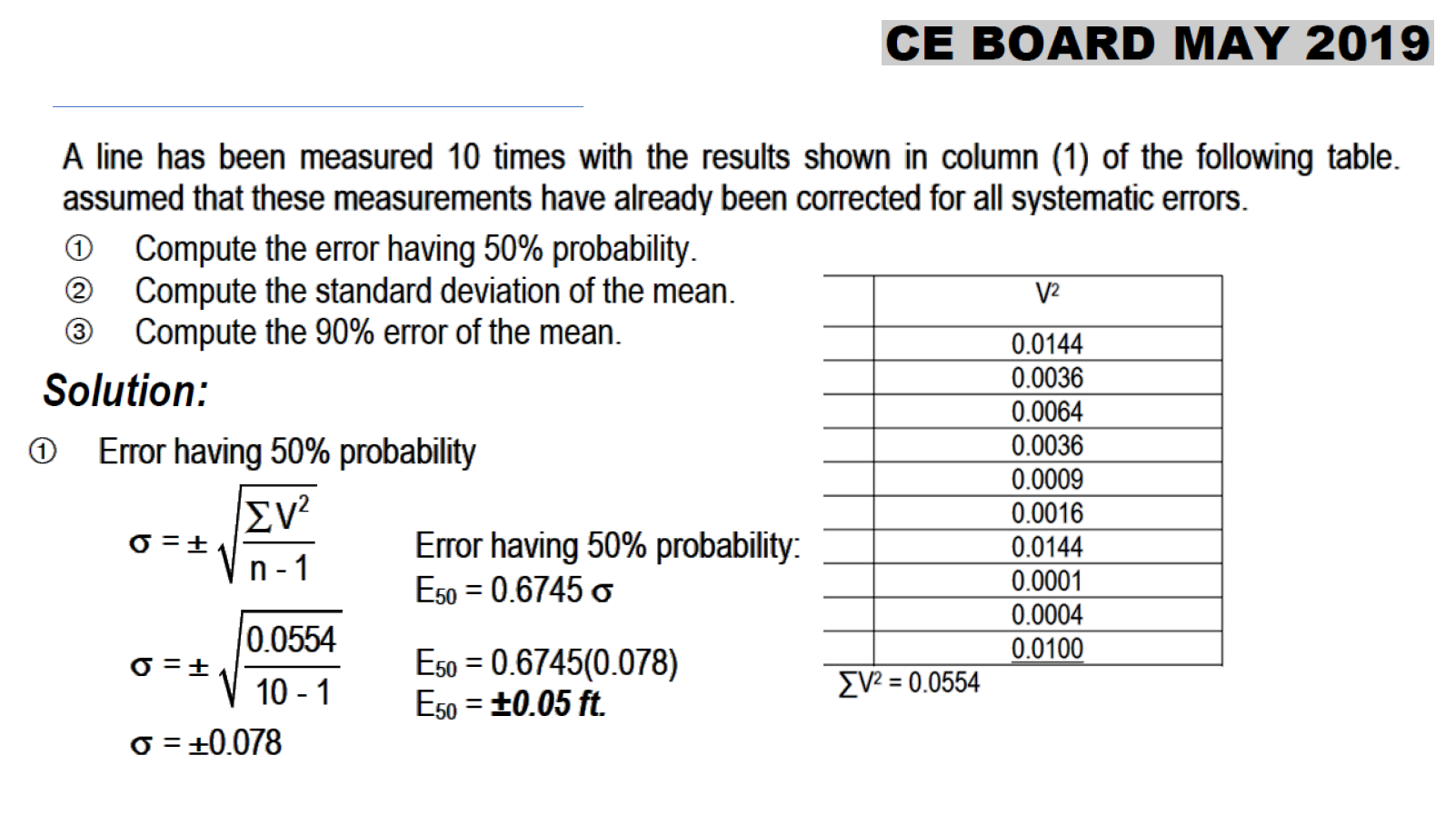
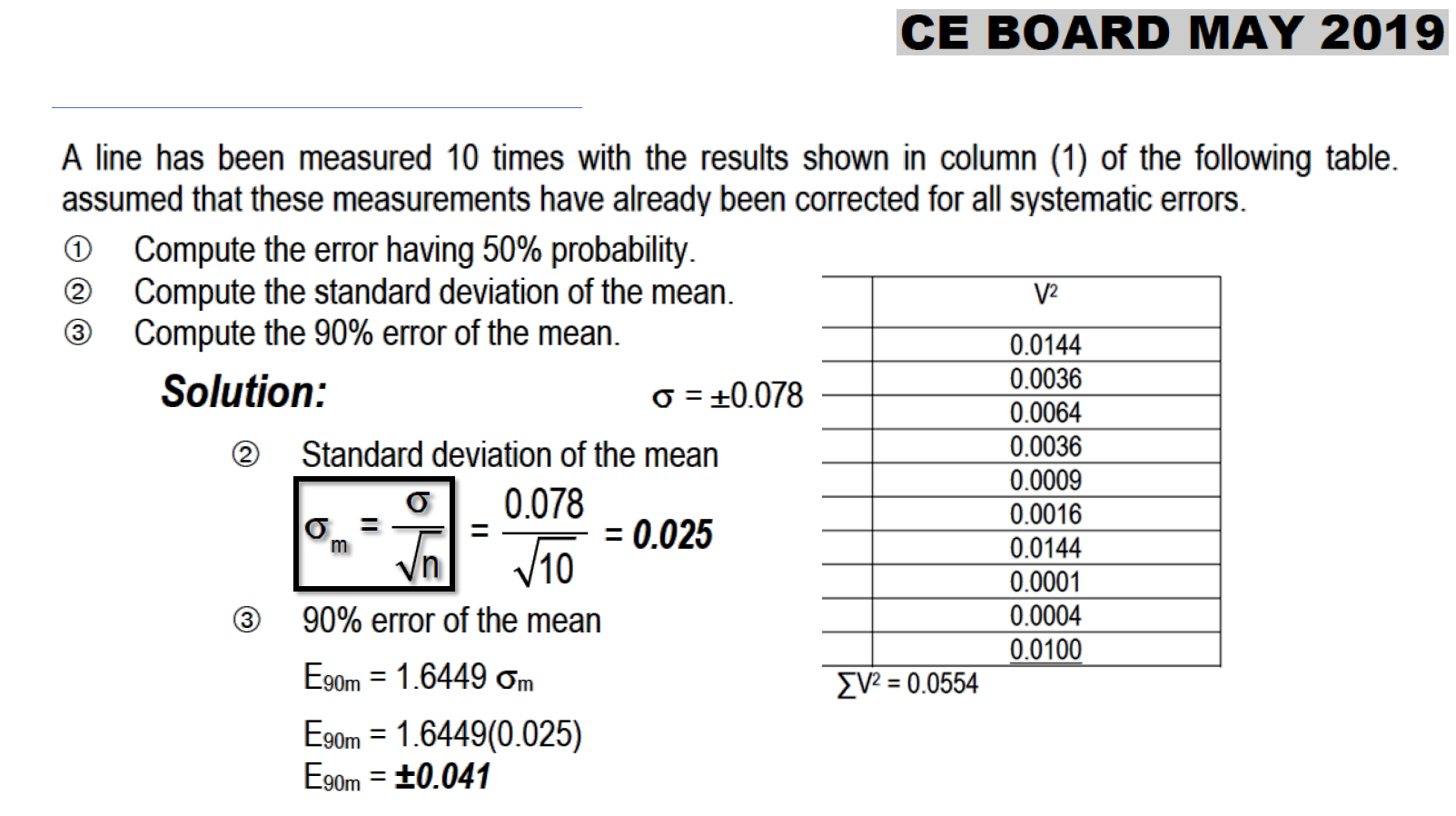
A line has been measured 10 times with the results shown in column 1, assuming that the measurements have already been corrected for all systematic errors.
1. Compute the error having 50% probability
2. Compute the standard deviation of the mean.
3. Compute the 90% error of the mean.
See images:
Refer to the image shown:
See images:
Refer to the image shown:
See images:
Refer to the image shown:
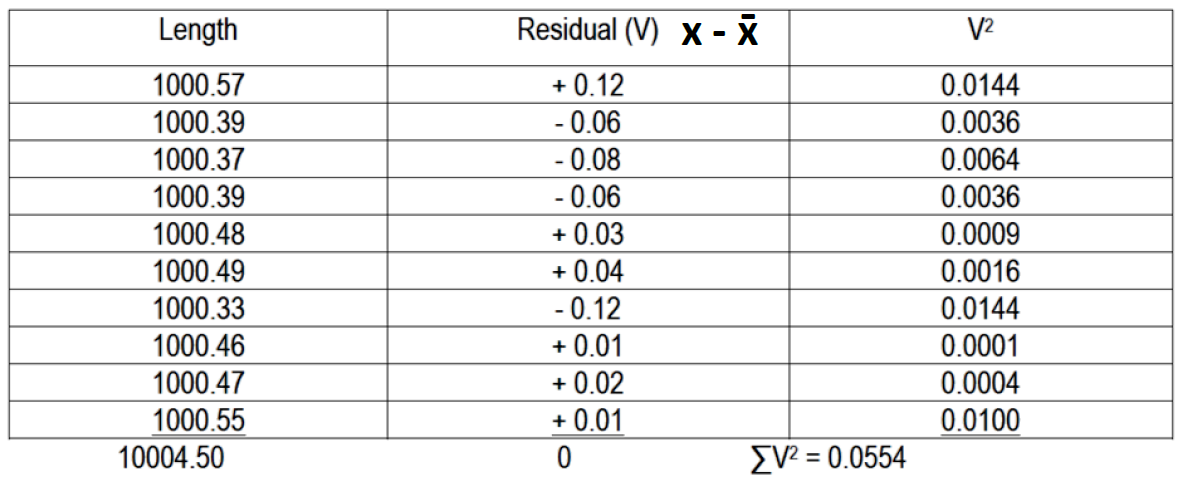
See images:
