


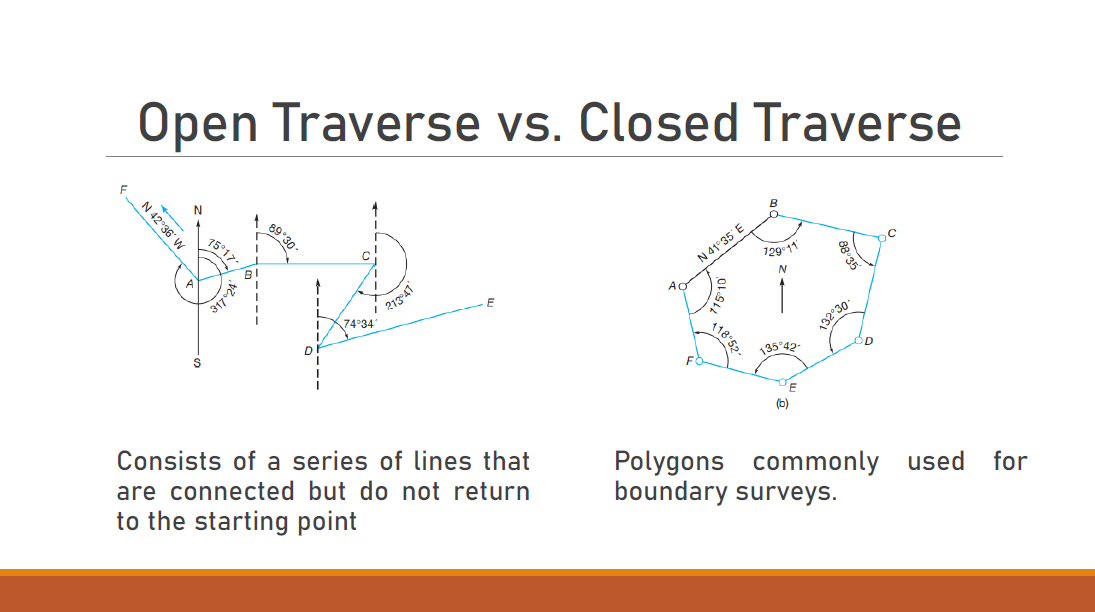




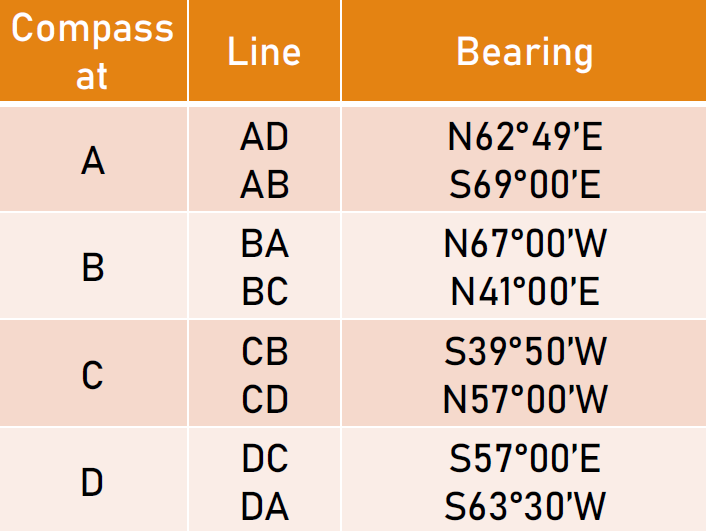
The following bearings are taken on a closed compass traverse. Assume the observed bearing of line AB to be correct.
a. Compute the error in closure.
b. Compute the corrected bearing of the lines.


See images:

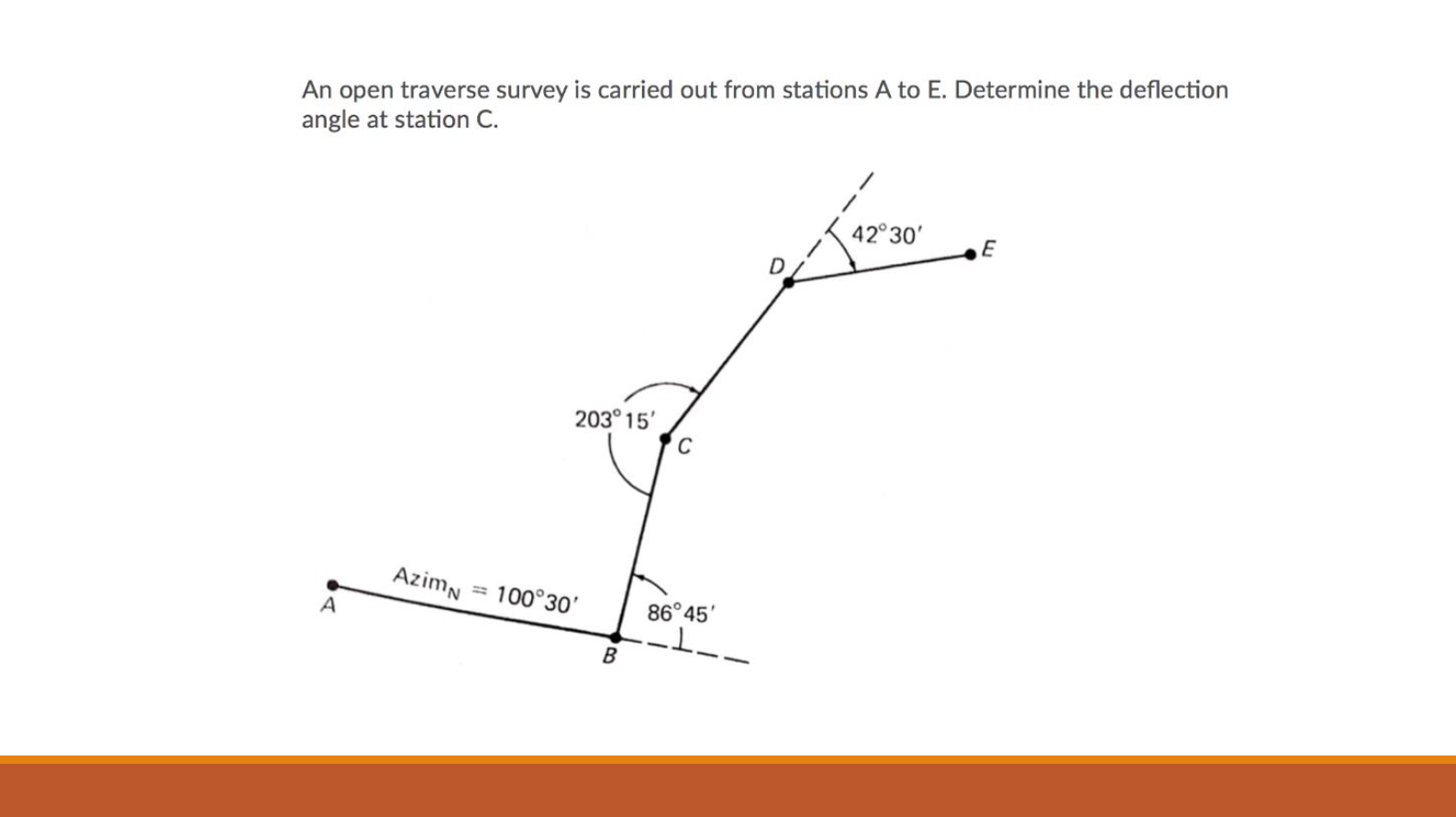
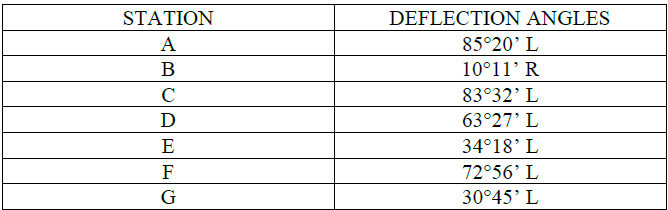
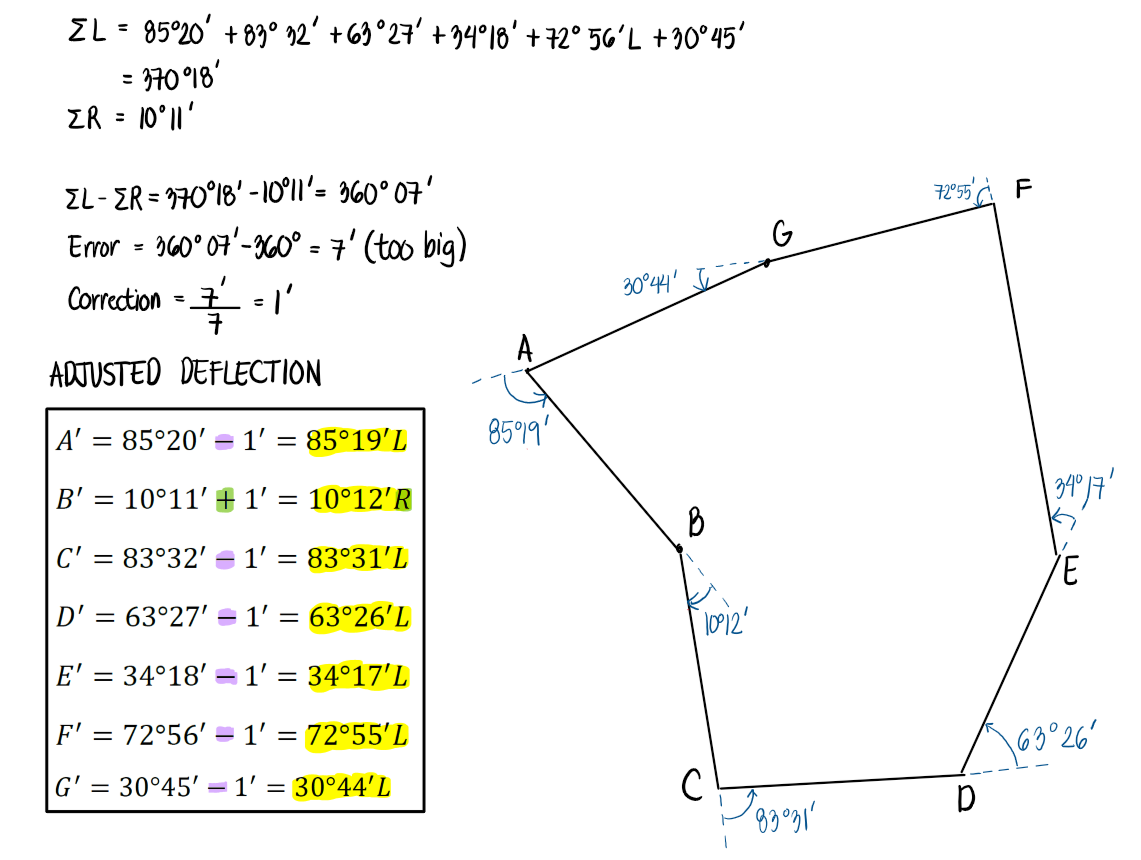
In the deflection angle traverse with a transit survey data below, find the corrected bearing of the lines. Bearing of line AB is N51°37'W.
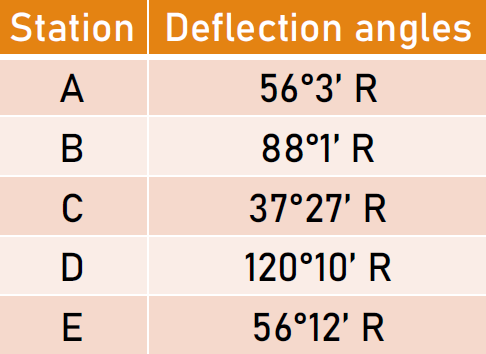


See images:




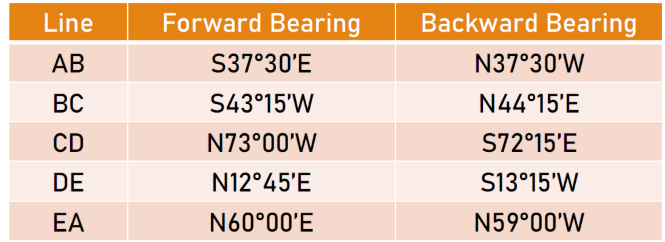
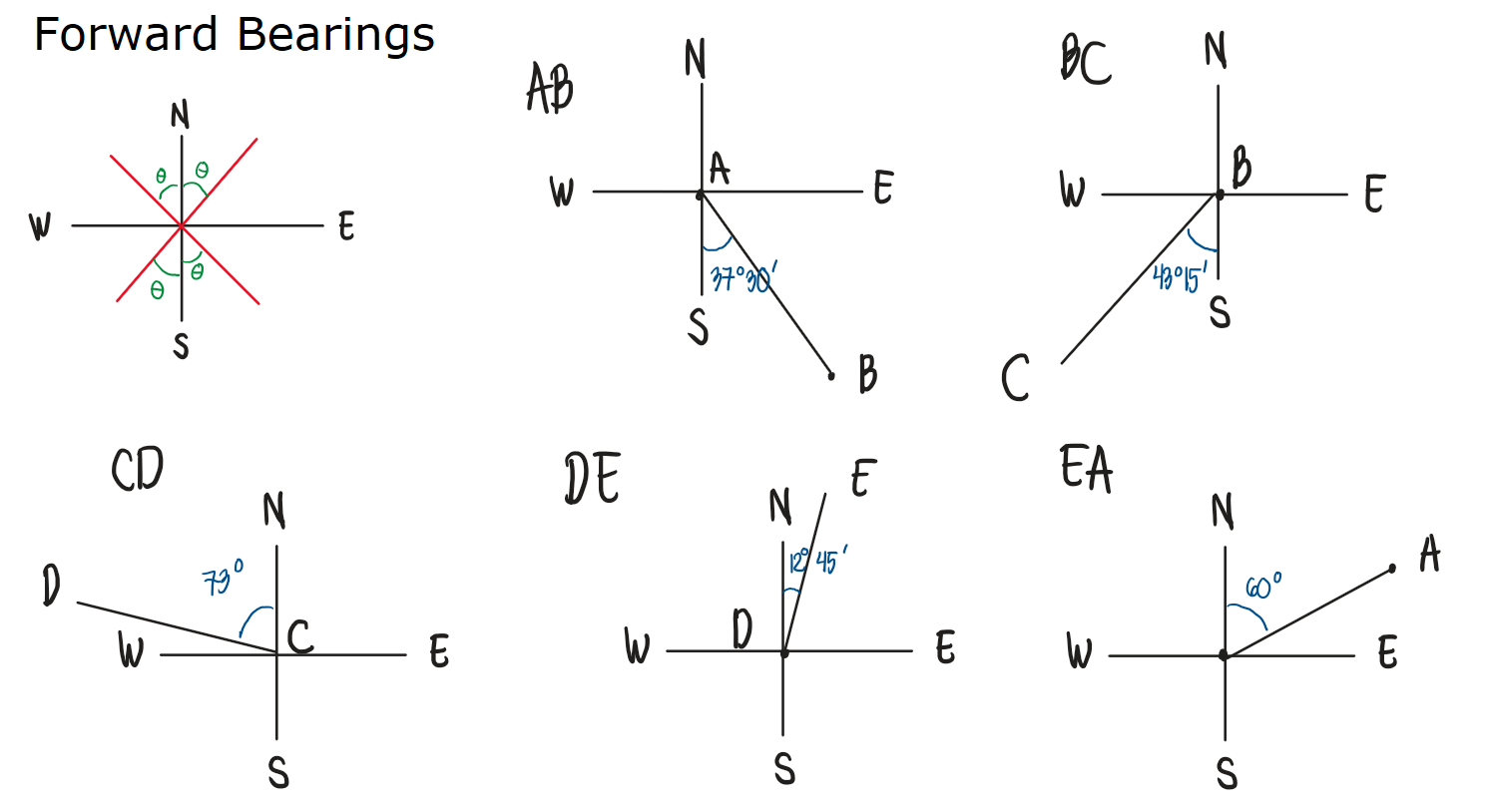
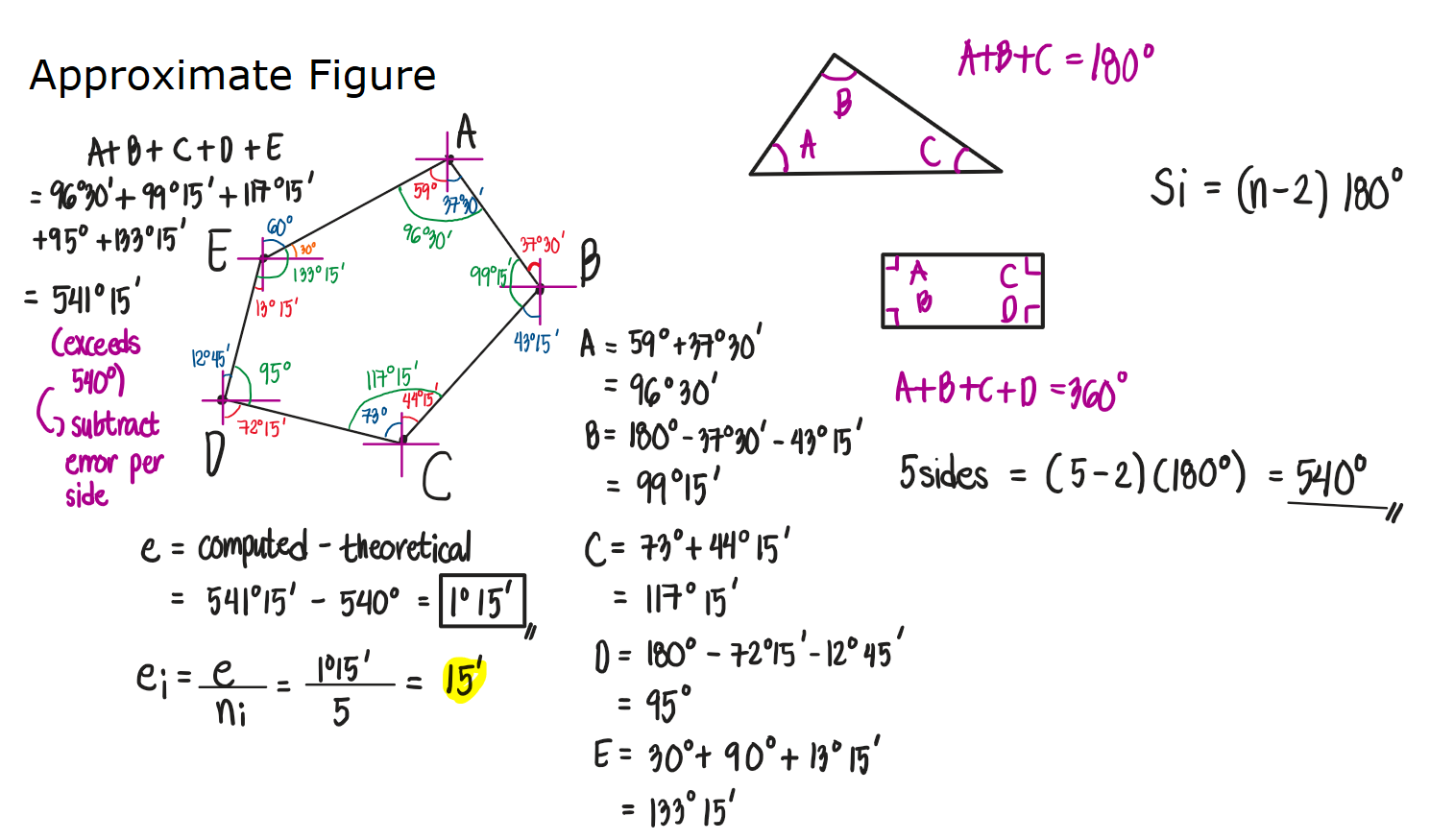
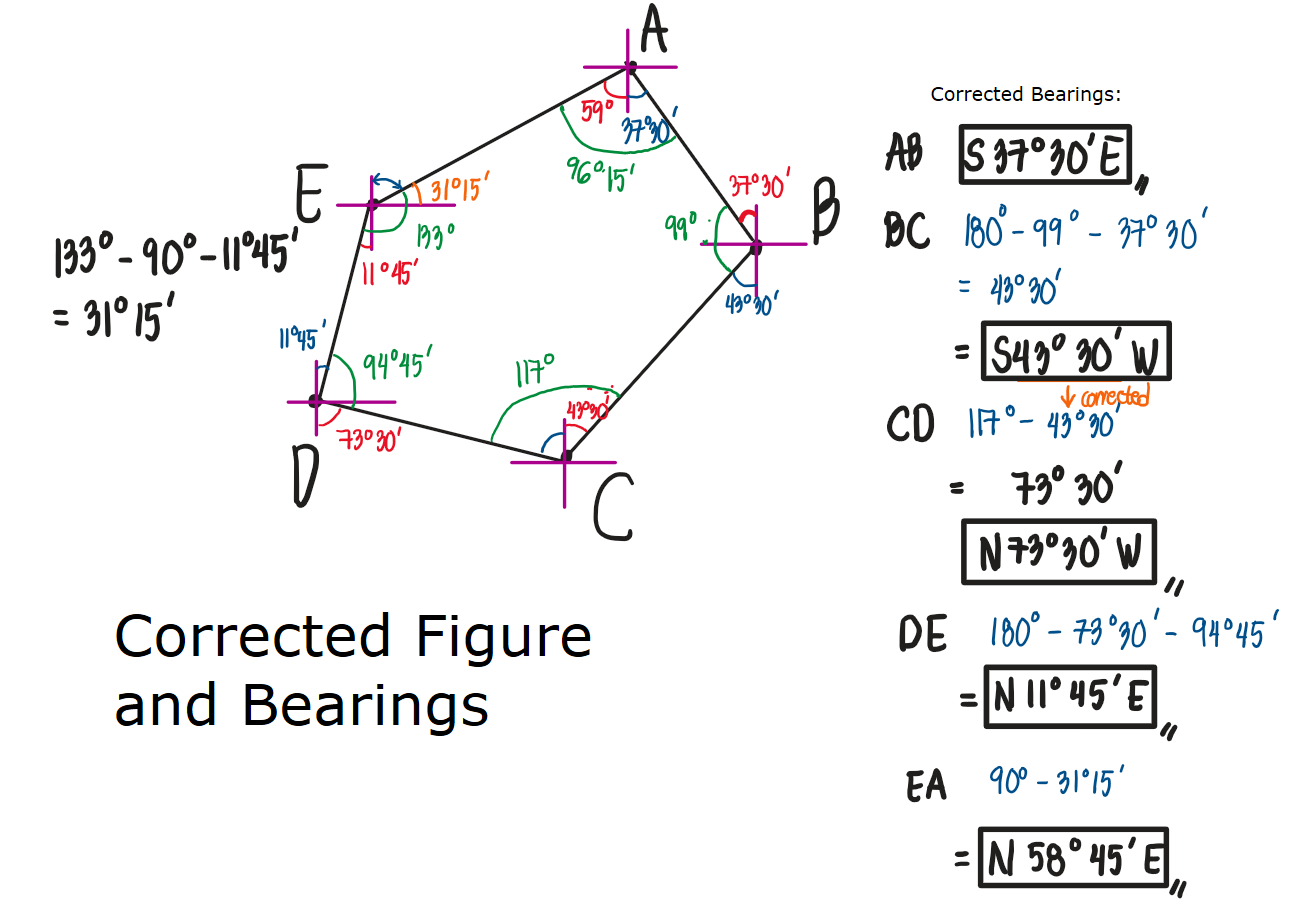
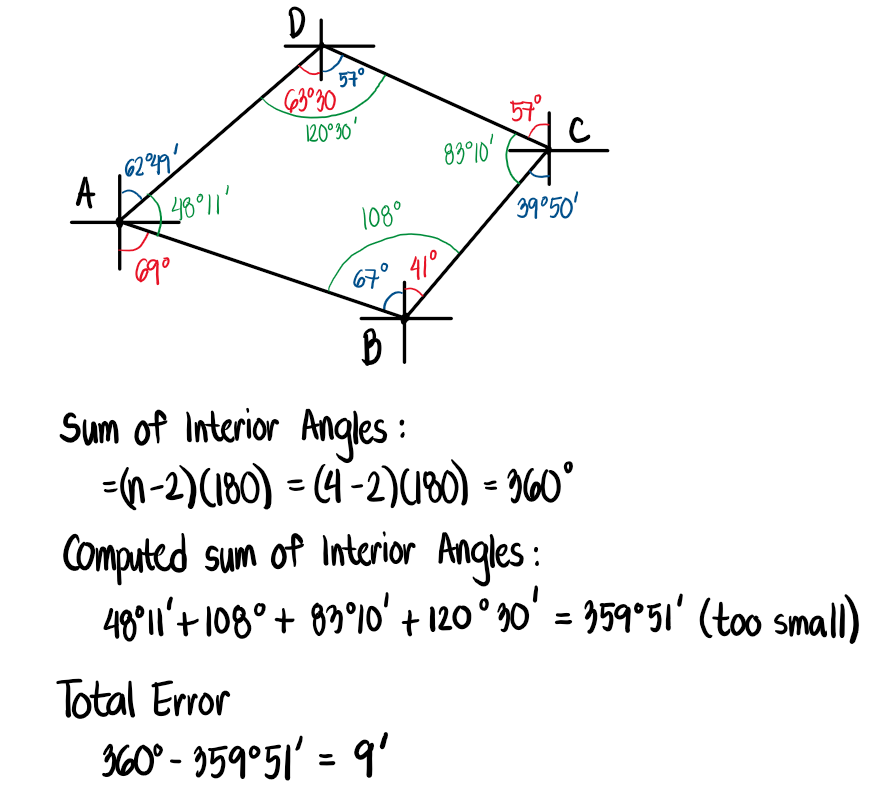
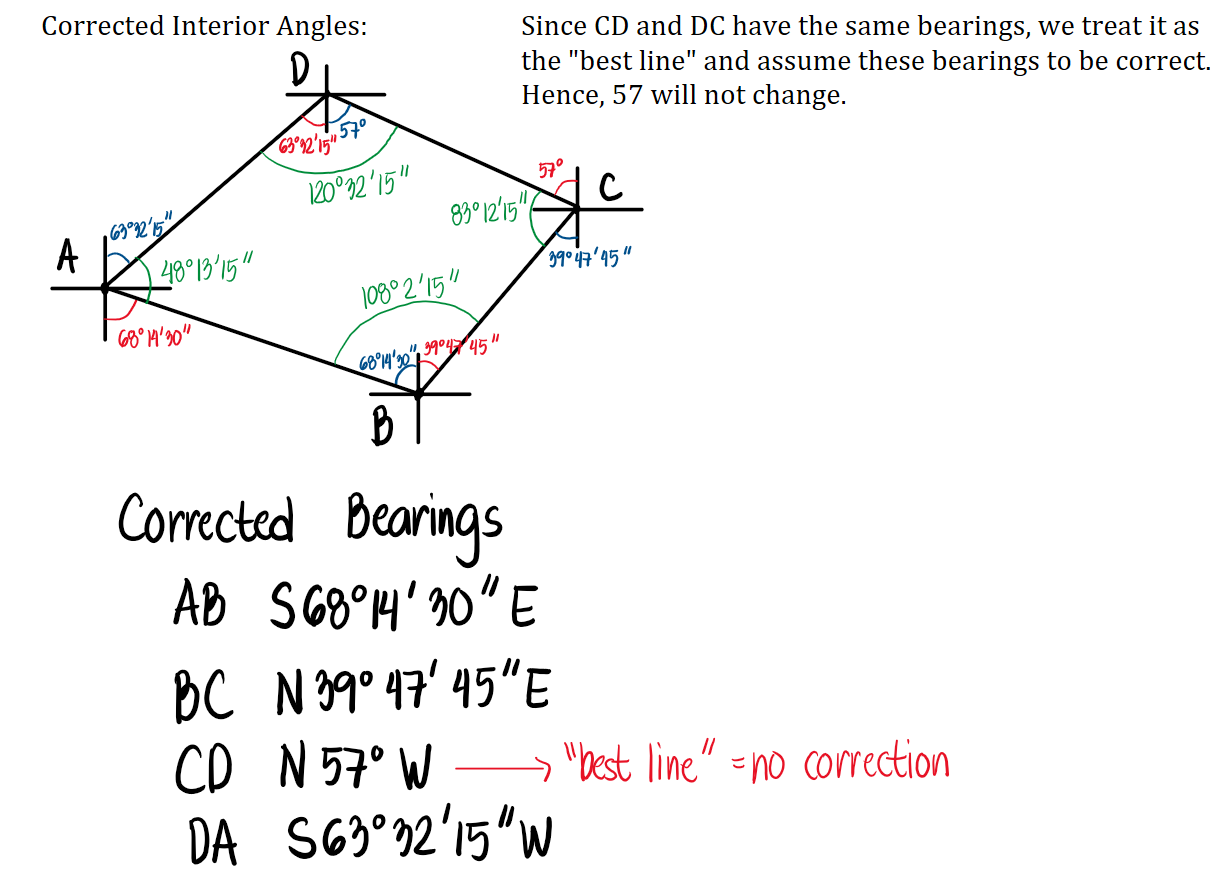
An engineer's notebook gives the observed magnetic bearings of the following traverse. Compute the corrected bearings of the lines.


See images:


| Line | Forward Bearing | Backward Bearing |
|---|---|---|
| AB | N 30°30′ W | S 32°15′ E |
| BC | S 80°45′ W | N 82°45′ E |
| CD | S 53°00′ W | N 50°15′ E |
| DE | S 13°00′ W | N 11°30′ E |
| EA | N 66°30′ E | S 69°30′ W |



Solution:
Compute the Central Angle
A = 180° − 30°30′ − 69°30′ = 80°00′
B = 32°15′ + 80°45′ = 113°00′
C = 180° − 82°45′ + 53°00′ = 150°15′
D = 180° − 50°15′ + 13°00′ = 142°45′
E = 66°30′ − 11°30′ = 55°00′
Sum of Interior Angles = (5 − 2)180° = 540°
Σ angles = 80° + 113° + 150°15′ + 142°45′ + 55° = 541°
Error = 541° − 540° = 1° (too big --> subtract the error on each side)
Correction = 1° / 5 = 12′
| Line | Forward Azimuth | Backward Azimuth | Difference |
|---|---|---|---|
| AB | 149°30′ | 327°45′ | 178°15′ |
| BC | 80°45′ | 262°45′ | 182°00′ |
| CD | 53°00′ | 230°15′ | 177°15′ |
| DE | 13°00′ | 191°30′ | 178°30′ |
| EA | 246°30′ | 69°30′ | 177°00′ |
| Line | Bearing | Azimuth |
|---|---|---|
| DE | S 13°45′ W | 13°45′ |
| EA | 13°45′ + 54°48′ = N 68°33′ E | 248°33′ |
| AB | 180° − 68°33′ − 79°48′ = N 31°39′ W | 148°21′ |
| BC | 112°48′ − 31°39′ = S 81°09′ W | 81°09′ |
| CD | 150°03′ + 81°09′ − 180° = S 51°12′ W | 51°12′ |




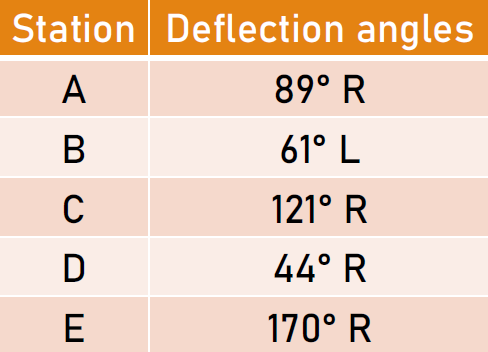
Given the following deflection angles of a closed traverse, compute the bearing of all the lines if the bearing of AB is S40°E.


The corrected deflection angles are shown below. By analyzing the observed values, it will be identified that the sum of the left deflection angles must be reduced and the sum of the right deflection angles must be increased.
In other words, the summation of the left deflection angles is larger than the summation of the right deflection angles, and since the total angle exceeds 360°, we need to subtract the correction for the larger summation (left) and add the correction to the lesser summation (right).
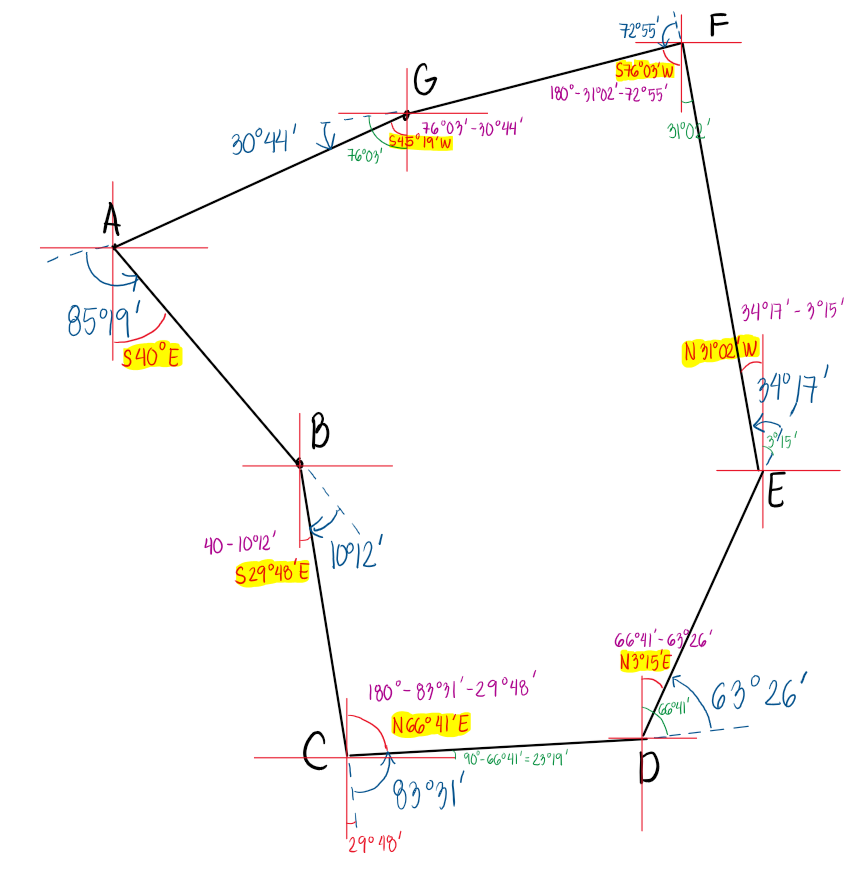


Following are the observed deflection angles of a closed traverse. Find the corrected bearing of the lines if the bearing of line AB is S31°E.


See images:




Refer to the image shown:



See images:




Refer to the image shown:



See images:



