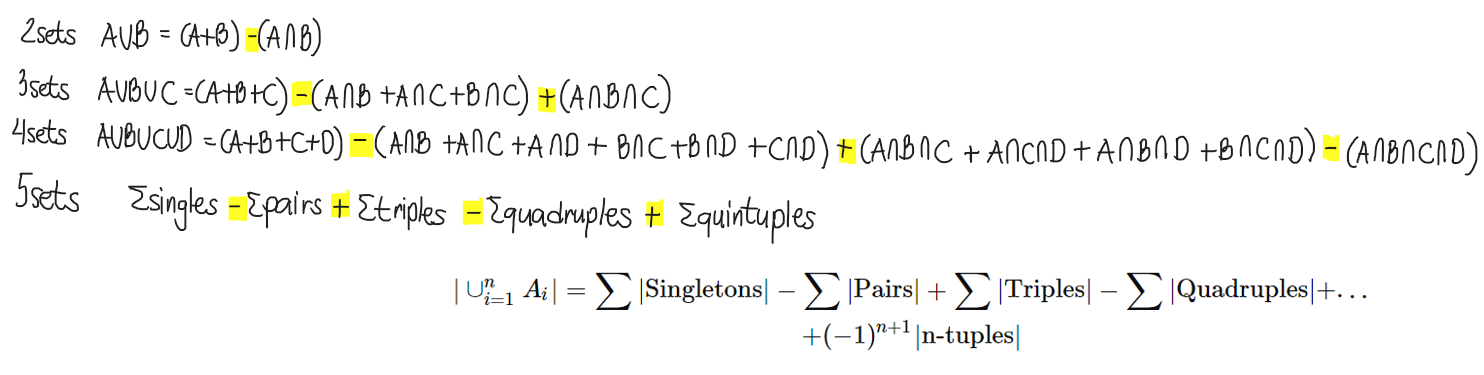Sets

This section summarizes the essential concepts and formulas for Sets, Subsets, Set Operations, and the Principle of Inclusion and Exclusion, foundational for understanding Algebra at the engineering level.

A set is a collection of distinct elements, usually denoted by capital letters. The number of elements in a set is called its cardinality and is written as $|S|$ or $n(S)$.

Common Sets

$\{\}$ or $\emptyset$ – Null set (no elements)
$\{x\}$ – Unit set (one element)
$P$ – Set of all prime numbers
$N$ – Natural numbers
$Z$ – Integers
$Q$ – Rational numbers
$R$ – Real numbers
$C$ – Complex numbers
$H$ – Quaternions

Subsets

If every element of set $A$ is also in $B$, we write:

$$ A \subseteq B $$

A proper subset is one where $A \subseteq B$ but $A \ne B$.

Complement and Relative Complement

Absolute Complement: All elements not in $A$

$$ A' \quad \text{or} \quad A^c $$

Relative Complement: All elements in $A$ but not in $B$

$$ A \setminus B $$

Set Operations

Union: All elements in $A$ or $B$

$$ A \cup B $$

Intersection: All elements common to $A$ and $B$

$$ A \cap B $$

Principle of Inclusion and Exclusion

This principle helps count elements in the union of overlapping sets while avoiding overcounting.

$$ \left| \bigcup_{i=1}^{n} A_i \right| = \sum_{i=1}^{n} |A_i| - \sum_{1 \le i < j \le n} |A_i \cap A_j| + \sum_{1 \le i < j < k \le n} |A_i \cap A_j \cap A_k| - \cdots + (-1)^{n+1} \left| A_1 \cap A_2 \cap \cdots \cap A_n \right| $$

$$ \begin{aligned} |A \cup B \cup C \cup D| &= |A| + |B| + |C| + |D| \quad \text{(all singletons)} \\\\ &\quad - \left( |A \cap B| + |A \cap C| + |A \cap D| + |B \cap C| + |B \cap D| + |C \cap D| \right) \quad \text{(all pairs)} \\\\ &\quad + \left( |A \cap B \cap C| + |A \cap B \cap D| + |A \cap C \cap D| + |B \cap C \cap D| \right) \quad \text{(all triples)} \\\\ &\quad - |A \cap B \cap C \cap D| \quad \text{(all quadruples)} \end{aligned} $$

This formula is especially useful in solving problems involving 2 or more overlapping sets, common in surveys, probability, and classification tasks in engineering.

Problem 1:

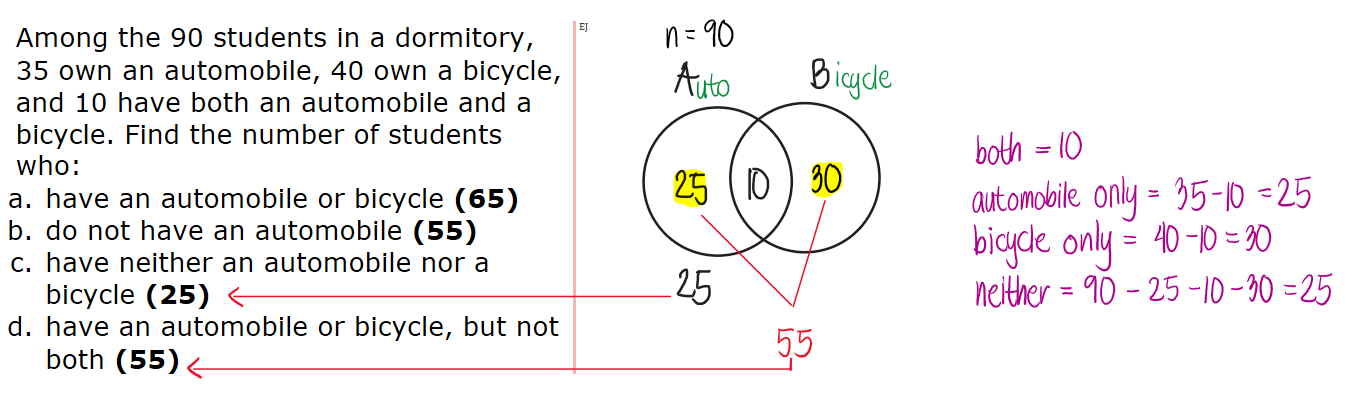
Among the 90 students in a dormitory, 35 own an automobile, 40 own a bicycle, and 10 have both an automobile and a bicycle. Find the number of students who:
a. have an automobile or bicycle
b. do not have an automobile
c. have neither an automobile nor a bicycle
d. have an automobile or bicycle, but not both

See images:

Problem 2:

In a consumer market, 85% of those surveyed liked at least one of three products: 1, 2, or 3. 50% of those asked liked product 1, 30% liked product 2, and 20% liked product 3. If 5% of the people in the survey liked all three of the products, what percentage of the survey participants liked more than one of the three products?
A. 10%
B. 15%
C. 25%
D. 30%

See images:

Problem 3:

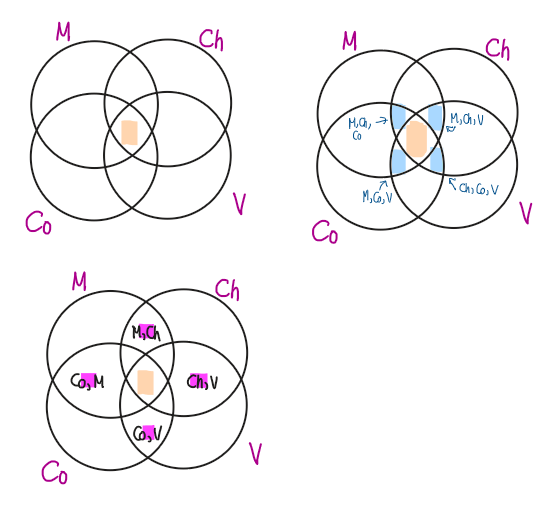
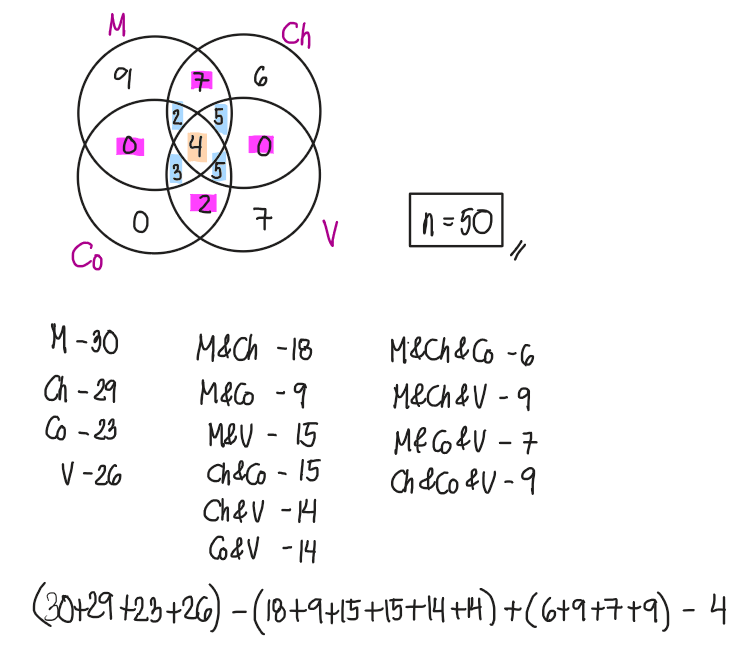
In a coffee shop that offers four kinds of drinks: Mocha, Choco, Coffee, and Vanilla. Thirty ordered Mocha. 29 ordered Choco. 23 ordered Coffee. 26 ordered Vanilla. Eighteen ordered Mocha and Choco, 9 ordered Mocha and Coffee, 15 ordered Mocha and Vanilla, 15 ordered Choco and Coffee, 14 ordered Choco and Vanilla, and 14 ordered Coffee and Vanilla. Six ordered Mocha, Choco, and Coffee; 9 ordered Mocha, Choco, and Vanilla; 7 ordered Mocha, Coffee, and Vanilla; and 9 ordered Choco, Coffee, and Vanilla. Four ordered Mocha, Choco, Coffee, and Vanilla. Assuming that each person ordered one of a kind for each purchase, determine the total number of people who ordered.
A. 50
B. 40
C. 75
D. 100