Partial fraction decomposition is a method used to rewrite rational expressions—fractions where both numerator and denominator are polynomials—into a sum of simpler fractions. This technique is essential in calculus, Laplace transforms, and system analysis in engineering.
Where $P(x)$ and $Q(x)$ are polynomials, and the degree of the numerator is less than the degree of the denominator.
If the denominator can be factored, the rational expression can be decomposed into a sum of simpler terms whose denominators match those factors. This makes integration and algebraic manipulation easier.
This decomposition method transforms complex expressions into manageable parts for integration, inverse transforms, or system modeling in engineering contexts.









Perform partial fraction decomposition for the following function: $$\frac{9x+2}{(x+2)(3x-2)}$$



See images:




Perform partial fraction decomposition for the following function: $$\frac{5x^2-25x+8}{(3x+2)(x^2-6x+9)}$$



See images:




Determine the value of A, B, and C. $$\frac{2x^2+x+1}{(x^3+x)}$$



See images:




Determine the value of A, B, C, and D. $$\frac{3x^2+5x+5}{(x^2+1)^2}$$



See images:




Determine the value of A, B, C, D, and E. $$\frac{4x^4-7x^3+5x^2-x+1}{(2x-1)(x^2-x+1)^2}$$



See images:




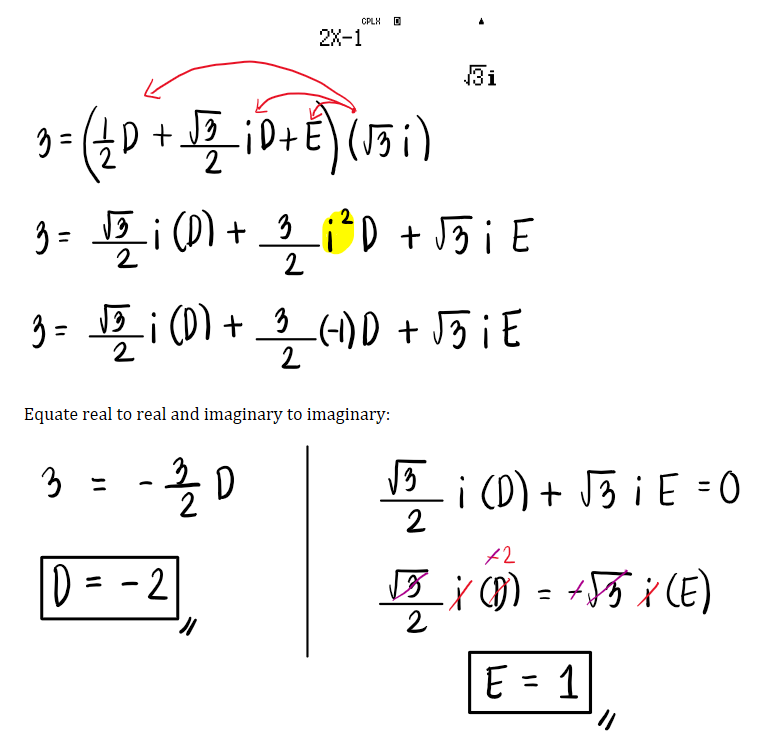

Refer to the image shown:



See images:




Refer to the image shown:



See images:




Refer to the image shown:



See images:



