CE Board Exam Randomizer

⬅ Back to Subject Topics

Number Problems

Number problems often involve finding unknown values that satisfy several conditions simultaneously. These conditions may include:

The key steps are:

  1. Assign variables to represent each unknown number.
  2. Translate the conditions into equations.
    For example:
    • “The sum of the three numbers is 51” becomes:
      $x + y + z = 51$
    • “The first number divided by the second gives a quotient of 2 and remainder 5” becomes:
      $x = 2y + 5$
    • “The second divided by the third gives a quotient of 3 and remainder 2” becomes:
      $y = 3z + 2$
  3. Solve the system of equations step-by-step, often starting from the simpler equations and substituting into the more complex ones.
  4. Check the solution by substituting back into all original conditions.

These problems are a practical application of algebra and logical reasoning, where understanding how to model real statements into equations is just as important as solving them.

Concept Concept Concept Concept Concept Concept Concept Concept Concept

Problem 1:

The sum of the three numbers is 51. If the first number is divided by the second, the quotient is 2 and the remainder 5; but if the second number is divided by the third, the quotient is 3 and the remainder 2. Determine the numbers.

Number Problems | Algebra – Problem 1: – Diagram Number Problems | Algebra – Problem 1: – Diagram Number Problems | Algebra – Problem 1: – Diagram

See images:

Number Problems | Algebra – Problem 1: – Diagram Number Problems | Algebra – Problem 1: – Diagram Number Problems | Algebra – Problem 1: – Diagram Number Problems | Algebra – Problem 1: – Diagram

Problem 2:

If the numerator of a certain fraction is increased by 2 and the denominator is increased by 1, the resulting fraction equals 1/2. If, however, the numerator is increased by 1 and the denominator decreased by 2, the resulting fraction equals 3/5 . Find the fraction.

Number Problems | Algebra – Problem 2: – Diagram Number Problems | Algebra – Problem 2: – Diagram Number Problems | Algebra – Problem 2: – Diagram

Number Problems | Algebra – Problem 2: – Diagram Number Problems | Algebra – Problem 2: – Diagram Number Problems | Algebra – Problem 2: – Diagram Number Problems | Algebra – Problem 2: – Diagram

Problem 3:

The ten's digit of a certain number is 3 less than the unit's digit. If the number is divided by the sum of the digits, the quotient is 4 and the remainder is 3. What is the original number?

Number Problems | Algebra – Problem 3: – Diagram Number Problems | Algebra – Problem 3: – Diagram Number Problems | Algebra – Problem 3: – Diagram

See images:

Number Problems | Algebra – Problem 3: – Diagram Number Problems | Algebra – Problem 3: – Diagram Number Problems | Algebra – Problem 3: – Diagram Number Problems | Algebra – Problem 3: – Diagram

Problem 4:

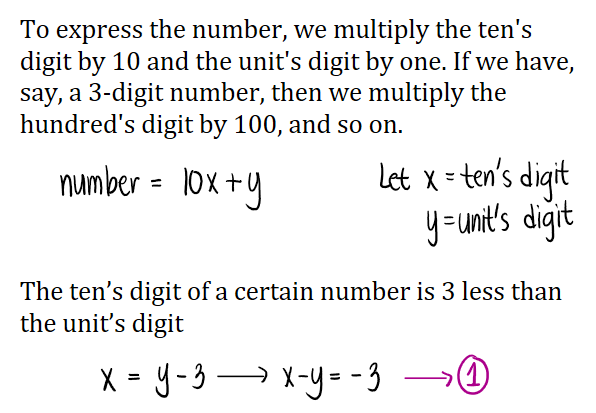
A number is expressed by 3 digits, which are in arithmetic progression. If the number is divided by the sum of the digits, the quotient is 26 and if 198 is to be added to the number, the digits will be reversed. Find the ten's digit.

Number Problems | Algebra – Problem 4: – Diagram Number Problems | Algebra – Problem 4: – Diagram Number Problems | Algebra – Problem 4: – Diagram

See images:

Number Problems | Algebra – Problem 4: – Diagram Number Problems | Algebra – Problem 4: – Diagram Number Problems | Algebra – Problem 4: – Diagram Number Problems | Algebra – Problem 4: – Diagram

Problem 5:

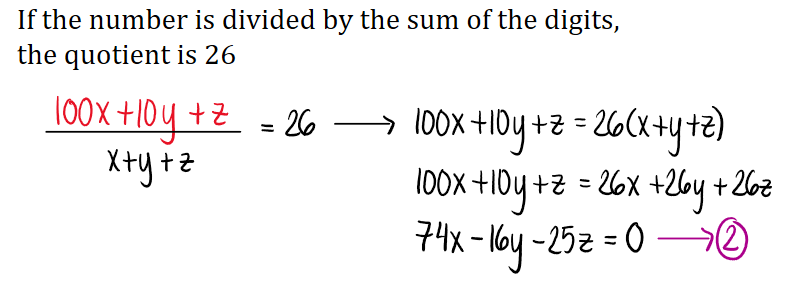
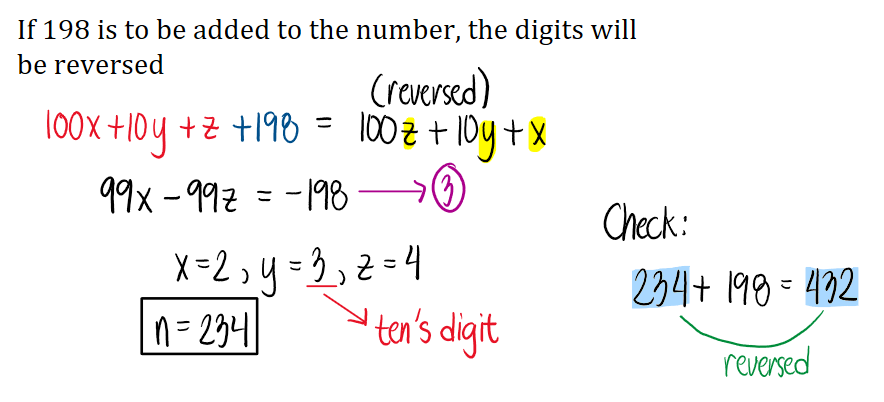
The sum of the ages of the three brothers is 63. If their ages are consecutive integers, what is the age of the eldest brother?

Number Problems | Algebra – Problem 5: – Diagram Number Problems | Algebra – Problem 5: – Diagram Number Problems | Algebra – Problem 5: – Diagram

See images:

Number Problems | Algebra – Problem 5: – Diagram Number Problems | Algebra – Problem 5: – Diagram Number Problems | Algebra – Problem 5: – Diagram Number Problems | Algebra – Problem 5: – Diagram
Scroll to zoom